 |
Seminaire MAX de calcul formel |  |
Le séminaire MAX a lieu dans le bâtiment Alan Turing sur le campus de l'École polytechnique. Cliquez ici pour plus d'informations sur comment nous joindre.
Prochaines séances
29 septembre 2025
Matryoshka Arithmetic
Heure: from 11h00 to 12h00
Salle: Grace Hopper
How to automatically determine reliable error bounds for a numerical computation? One traditional approach is to systematically replace floating point approximations by intervals or balls that are guaranteed to contain the exact numbers of interest. However, operations on intervals or balls are more expensive than operations on floating point numbers, so this approach involves a non-trivial overhead. In this talk, we present several approaches to remove this overhead, under the assumption that the function f that we wish to evaluate is given as a straight-line program (SLP). We will first study the case when the arguments of our function lie in fixed balls. For polynomial SLPs, we next consider the “global” case where this restriction on the arguments is removed.
Based on joint work with
6 octobre 2025
Fast multivariate integration in D-modules
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Not all integrals can be expressed in closed form using elementary functions, as shown by Liouville's theorem. In contrast, the integral of a holonomic/D-finite function is always holonomic/D-finite, that is the integral of a function satisfying sufficiently many linear differential equations (LDEs) with polynomial coefficients also satisfies such a system of LDEs. This makes the holonomic and D-finite frameworks particularly relevant for symbolic integration.
I will address two central algorithmic problems in this field: the problem of integration with parameters, where one seeks a differential equation satisfied by a parametric integral, and the reduction problem, where the goal is to find linear relations between integrals. Two distinct approaches exist, the D-finite one and the holonomic one. The D-finite approach has been the most studied one and offers efficient algorithms, but it lacks the full expressivity of the holonomic setting, which can handle a broader class of integrals and particularly those over semi-algebraic sets. However, the current algorithms developed for the holonomic setting have a prohibitive computational cost. I will present a new reduction algorithm working in a mixed approach, aiming to balance the efficiency of D-finiteness with the expressivity of holonomy. This reduction is inspired by the Griffiths-Dwork method for rational functions and yields similarly an algorithm for the problem of parametric integration.
As an application, I will present the computation of a differential equation for the generating function of 8-regular graphs, which was out of reach so far.
This is a joint work with my PhD advisors
1 décembre 2025
TBA
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
TBD
Séances précédentes
23 juin 2025
Projective variety recovery from unknown linear projections
Heure: from 10h45 to 11h45
Salle: Grace Hopper
We study how a smooth irreducible algebraic variety 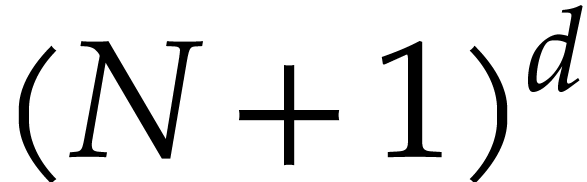 of dimension
of dimension 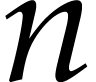 embedded in
embedded in 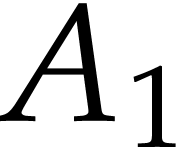 (with
(with 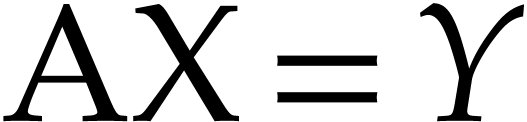 ), which degree is
), which degree is 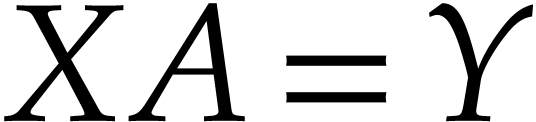 ,
can be recovered using two projections from unknown points onto
unknown hyperplanes. The centers and the hyperplanes of projection are
unknown: the only input is the defining equations of each projected
varieties. We show how both the projection operators and the variety
in
,
can be recovered using two projections from unknown points onto
unknown hyperplanes. The centers and the hyperplanes of projection are
unknown: the only input is the defining equations of each projected
varieties. We show how both the projection operators and the variety
in 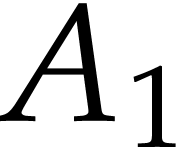 can be recovered modulo some action of the
group of projective transformations of
can be recovered modulo some action of the
group of projective transformations of 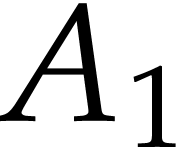 . This
configuration generalizes results obtained in the context of curves
embedded in
. This
configuration generalizes results obtained in the context of curves
embedded in  ([1]) and results concerning
surfaces embedded in
([1]) and results concerning
surfaces embedded in  ([2]).
([2]).
We show how in a generic situation, a characteristic matrix of the
pair of projections can be recovered. In the process we address
dimensional issues and as a result establish a necessary condition, as
well as a sufficient condition to compute this characteristic matrix
up to a finite-fold ambiguity. These conditions are expressed as
minimal values of the degree of the dual variety. Then we use this
matrix to recover the class of the couple of projections and as a
consequence to recover the variety. For a generic situation, two
projections define a variety with two irreducible components. One
component has degree 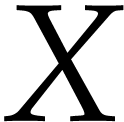 and the other has degree
and the other has degree
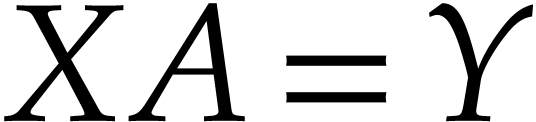 , being the original variety.
, being the original variety.
[1]
[2]  from two generic linear projections,
In Proceedings of the 36th International Symposium on Symbolic and
Algebraic Computation (ISSAC), 2011.
from two generic linear projections,
In Proceedings of the 36th International Symposium on Symbolic and
Algebraic Computation (ISSAC), 2011.
16 juin 2025
On the Existence of Principal Differential Ideals for Polynomial Derivations: Recent Advances and Computational Aspects
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
We restrict ourselves to the (seemingly) simple settings of polynomial
derivations with a focus on the long standing open problems pertaining
to the existence of principal differential ideals and their concise
representation. Those particular ideals play an important theoretical
role in the integrability of polynomial dynamical systems and have
found several applications (e.g. theoretical physics) since their
introduction in the seminal work of Gaston Darboux, almost 150 years
ago. We show that the coefficients of the (unique) generator have to
satisfy underlying recurrences that can be made explicit. This key
insight shed some light on the structure of such objects: not only it
allows to reason about their existence, it also suggest a completely
novel approach for their effective computation. This is a joint work
with
2 juin 2025
Resonances as a computational tool
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
A large toolbox of numerical schemes for dispersive equations has been established, based on different discretization techniques such as discretizing the variation-of-constants formula (e.g., exponential integrators) or splitting the full equation into a series of simpler subproblems (e.g., splitting methods). In many situations these classical schemes allow a precise and efficient approximation. This, however, drastically changes whenever non-smooth phenomena enter the scene such as for problems at low regularity and high oscillations. Classical schemes fail to capture the oscillatory nature of the solution, and this may lead to severe instabilities and loss of convergence. In this talk I present a new class of resonance based schemes. The key idea in the construction of the new schemes is to tackle and deeply embed the underlying nonlinear structure of resonances into the numerical discretization. As in the continuous case, these terms are central to structure preservation and offer the new schemes strong geometric properties at low regularity.
24 mars 2025
A computational proof of the Schmidt-Kolchin Conjecture
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Recently solved by  . A free family of polynomials containing exactly this
number of elements was unraveled by
. A free family of polynomials containing exactly this
number of elements was unraveled by
We show how the polynomials found by Reinhart can be dehomogenized and how the obtained sections form a generating family of the space of all sections, thus giving an alternative proof of the Schmidt-Kolchin Conjecture. The arguments are mainly algebraic and use determinants, linear algebra and monomial ordering.
This is joint work with
3 mars 2025
Elimination for Differential Dynamical Systems
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Differential dynamical systems appear in many applications in modeling and control theory. Frequently, for such dynamical systems, the task is to compute the minimal differential equation satisfied by a chosen coordinate. This task arises in particular in applications when only part of the solution data can be experimentally observed. As such, it is an important special case of more general differential elimination problems.
We present a new result, which provides explicit bounding hyperplanes
for the Newton polytope of such a minimal equation. The obtained
bounds are based on the degrees of a given dynamical system and are
proven to be sharp in “more than half the cases”. We
further use these bounds to design an algorithm for computing the
minimal equation following the evaluation-interpolation paradigm.
Using an implementation in Julia, we demonstrate that our
implementation of the algorithm can tackle problems which are out of
reach for the state-of-the-art software for differential elimination.
Lastly, we discuss potential future improvements to this algorithm
using sparse elimination theory. This is joint work with
31 janvier 2025
Fast basecases for arbitrary-size multiplication
Heure: from 11h00 to 11h45
Salle: Grace Hopper
(the talk is joint with the FLINT workshop, hence the unusual day of the week)
Multiple precision libraries like GMP typically use assembly-optimized loops for basecase operations on variable-length operands. We consider the alternative of generating lookup tables with hardcoded routines for many fixed sizes, e.g. for all multiplications up to 16 by 8 words. On recent ARM64 and x86-64 CPUs, we demonstrate up to a 2x speedup over GMP for basecase-sized multiplication. We pay special attention to the computation of approximate products and demonstrate up to a 3x speedup over GMP/MPFR for floating-point multiplication.
16 décembre 2024
Linear ordinary integro-differential systems: an algorithmic study
Heure: from 11h00 to 12h00
Salle: Grace Hopper
This talk aims to show that an algorithmic approach to linear polynomial ordinary integro-differential systems with separable kernels can be developed and implemented in a computer algebra system such as Maple.
To do this, we will introduce the ring  of
ordinary integro-differential operators with polynomial coefficients.
This ring contains the Weyl algebra
of
ordinary integro-differential operators with polynomial coefficients.
This ring contains the Weyl algebra 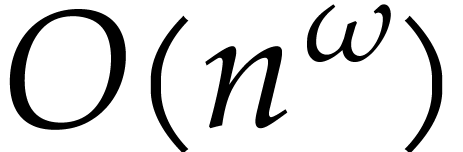 of
ordinary differential operators with polynomial coefficients. Unlike
of
ordinary differential operators with polynomial coefficients. Unlike
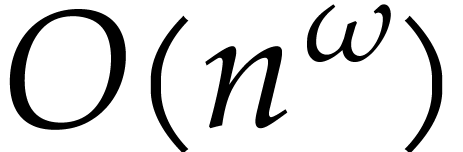 ,
,  has zero divisors and
is not Noetherian. However, in 2013,
has zero divisors and
is not Noetherian. However, in 2013,  is a coherent ring.
This result opens the possibility of an effective study of linear
polynomial integro-differential systems because these systems define
finitely presented left
is a coherent ring.
This result opens the possibility of an effective study of linear
polynomial integro-differential systems because these systems define
finitely presented left  modules and the
category of finitely presented modules over a coherent ring resembles
the category of finitely generated modules over a Noetherian ring.
However, the proof given by
modules and the
category of finitely presented modules over a coherent ring resembles
the category of finitely generated modules over a Noetherian ring.
However, the proof given by  can be obtained and
implemented. This result shows that the kernel of a matrix with
entries in
can be obtained and
implemented. This result shows that the kernel of a matrix with
entries in  can be computed effectively. Then,
an algorithmic elimination theory can be developed.
can be computed effectively. Then,
an algorithmic elimination theory can be developed.
Finally, we will show that  is effective in the
sense that linear systems of the form
is effective in the
sense that linear systems of the form 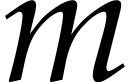 or
or 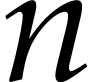 , where
, where 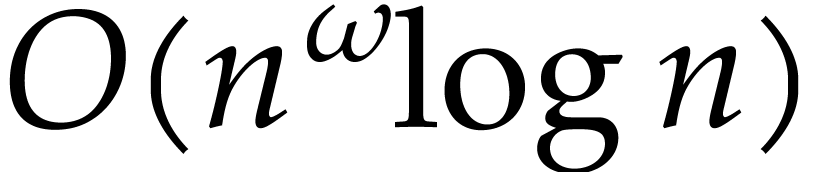 and
and  are two fixed matrices with entries in
are two fixed matrices with entries in  and
and
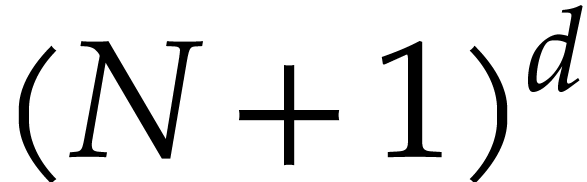 is an unknown matrix with entries in
is an unknown matrix with entries in  , are algorithmically solvable. Thus, methods of
homological algebra can be made effective and implemented, showing the
possibility of developing an algebraic analysis approach for this
class of linear functional systems.
, are algorithmically solvable. Thus, methods of
homological algebra can be made effective and implemented, showing the
possibility of developing an algebraic analysis approach for this
class of linear functional systems.
Explicit examples and calculations will illustrate the talk.
This work was done in collaboration with
4 novembre 2024
Computing Krylov iterates and characteristic polynomials in the time of matrix multiplication
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
This talk describes recent work with 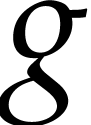 over a field, we will
describe two main algorithms. The first one computes the
characteristic polynomial within the same asymptotic complexity as the
multiplication of two
over a field, we will
describe two main algorithms. The first one computes the
characteristic polynomial within the same asymptotic complexity as the
multiplication of two 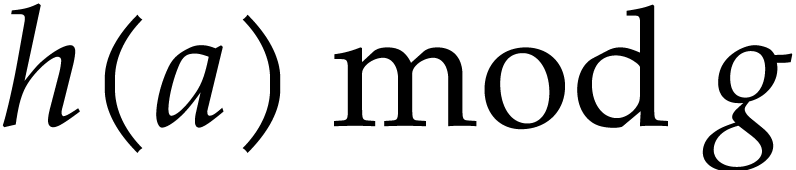 matrices, that is, in
matrices, that is, in
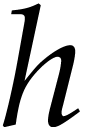 operations in the field. The second one takes
an additional list of
operations in the field. The second one takes
an additional list of 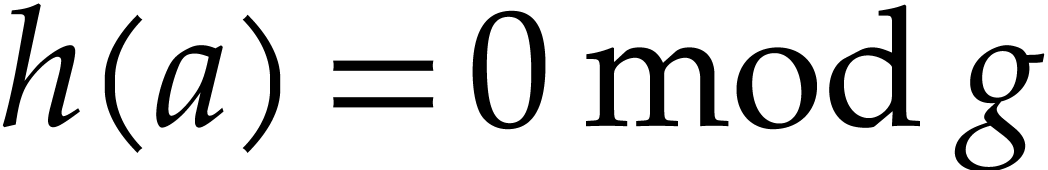 vectors and computes a
Krylov basis associated to
vectors and computes a
Krylov basis associated to 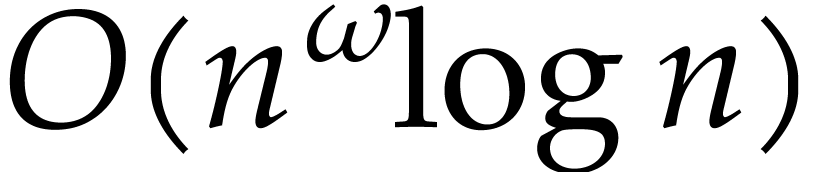 and these vectors,
also in
and these vectors,
also in 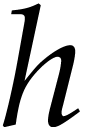 assuming
assuming 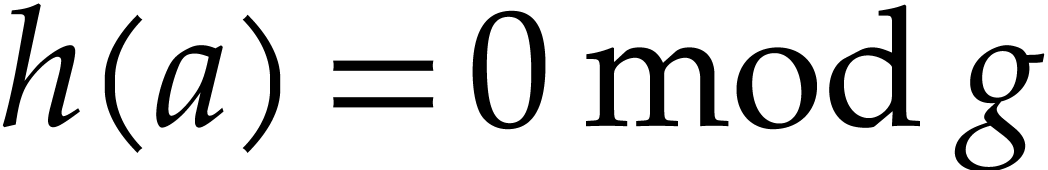 is
not too close to
is
not too close to 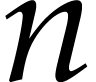 . These two related problems
had previously been solved in complexity
. These two related problems
had previously been solved in complexity 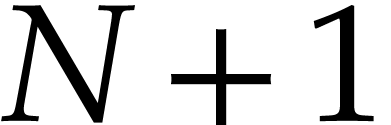 (
(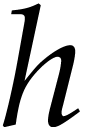 rely on genericity assumptions
or randomization (
rely on genericity assumptions
or randomization (
7 octobre 2024
Discretization error with Euler's method: Upper bound and applications
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Using the notion of (contractive) matrix measure, we give an upper bound on the discretization error with Euler's method. As applications, we give a method for ensuring the orbital stability of differential systems, and conditions on neural networks ensuring the convergence of the training error to 0.
23 septembre 2024
Puzzle Ideals for Grassmannians
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Puzzles, first introduced by
This talk is based on the joint work with
10 juin 2024
Partage de gâteaux sans-envie: une grande probabilité d'avoir un nombre de requêtes polynomial
Heure: from 11h00 to 12h00
Salle: Emmy Noether
Le problème du partage d'un gâteau entre 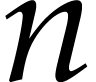 convives consiste à effectuer un découpage afin que
chaque convive reçoive sa «juste» part. Les
convives peuvent avoir des goûts différents et le
gâteau peut avoir plusieurs saveurs (chocolat, vanille, fraise,
etc.). Dans cet exposé, nous allons présenter comment le
problème du partage d'un gâteau peut être
modélisé et quel modèle de calcul est
utilisé pour étudier la complexité des
algorithmes. Nous verrons aussi qu'il existe différentes
notions de «juste part». Ensuite, nous verrons qu'il
existe un algorithme qui évite la jalousie entre les convives
et qui possède la qualité suivante: lorsque nous
considérons des convives «au hasard» alors la
probabilité de leur poser beaucoup de questions pour effectuer
le partage est petite.
convives consiste à effectuer un découpage afin que
chaque convive reçoive sa «juste» part. Les
convives peuvent avoir des goûts différents et le
gâteau peut avoir plusieurs saveurs (chocolat, vanille, fraise,
etc.). Dans cet exposé, nous allons présenter comment le
problème du partage d'un gâteau peut être
modélisé et quel modèle de calcul est
utilisé pour étudier la complexité des
algorithmes. Nous verrons aussi qu'il existe différentes
notions de «juste part». Ensuite, nous verrons qu'il
existe un algorithme qui évite la jalousie entre les convives
et qui possède la qualité suivante: lorsque nous
considérons des convives «au hasard» alors la
probabilité de leur poser beaucoup de questions pour effectuer
le partage est petite.
27 mai 2024 (Reporté à l'automne)
Faster modular composition of polynomials
Heure: from 11h00 to 12h00
Salle: Grace Hopper
This talk is about algorithms for modular composition of univariate
polynomials, and for computing minimal polynomials. For two univariate
polynomials 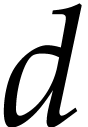 and
and 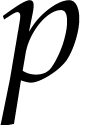 over a
commutative field, modular composition asks to compute
over a
commutative field, modular composition asks to compute 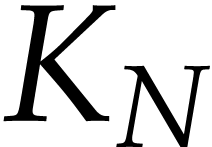 for some given
for some given  , while the
minimal polynomial problem is to compute
, while the
minimal polynomial problem is to compute  of
minimal degree such that
of
minimal degree such that 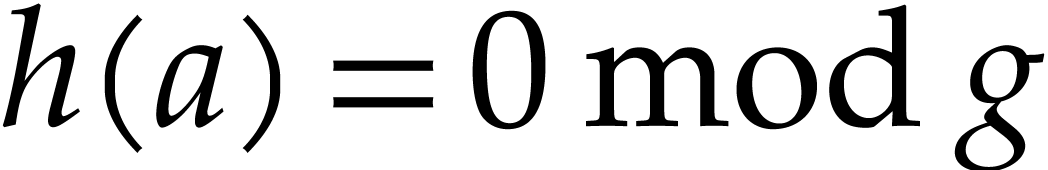 . We propose
algorithms whose complexity bound improves upon previous algorithms
and in particular upon
. We propose
algorithms whose complexity bound improves upon previous algorithms
and in particular upon 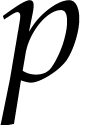 and
and 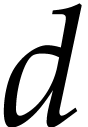 even
when using cubic-time matrix multiplication. Our improvement comes
from the fast computation of specific bases of bivariate ideals, and
from efficient operations with these bases thanks to fast univariate
polynomial matrix algorithms. We will also report on experimental
results using the Polynomial Matrix Library.
even
when using cubic-time matrix multiplication. Our improvement comes
from the fast computation of specific bases of bivariate ideals, and
from efficient operations with these bases thanks to fast univariate
polynomial matrix algorithms. We will also report on experimental
results using the Polynomial Matrix Library.
Contains joint work with
The corresponding article may be found here or here.
29 avril 2024
On the structure of differentially homogeneous polynomials
Heure: from 11h00 to 12h00
Salle: Grace Hopper
The goal of the talk is to discuss the structure of differentially
homogeneous polynomials in 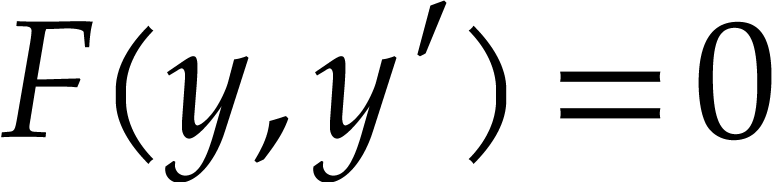 variables, and its
interpretation. We will mainly talk about the structure of vector
space: it is a graded algebra, whose
variables, and its
interpretation. We will mainly talk about the structure of vector
space: it is a graded algebra, whose 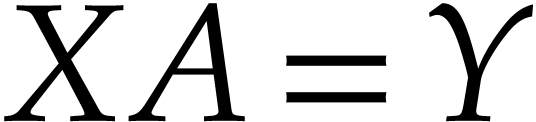 -th graded
component has dimension
-th graded
component has dimension  . This was predicted by
the so-called Schmidt-Kolchin conjecture. We will also (briefly) talk
about the expected structure as an algebra: it is an ongoing work,
being finalized.
. This was predicted by
the so-called Schmidt-Kolchin conjecture. We will also (briefly) talk
about the expected structure as an algebra: it is an ongoing work,
being finalized.
22 avril 2024
Factoring differential operators in positive characteristic through geometric means
Heure: from 15h30 to 16h30
Salle: Henri Poincaré
We focus on the porblem of factoring a given linear differential
operator, whose coefficients are elements of an algebraic function
field of characteristic  . After a brief
presentation of the previous works in that domain, in large part due
to
. After a brief
presentation of the previous works in that domain, in large part due
to  -Riccati
equation over a finite separable extension
-Riccati
equation over a finite separable extension 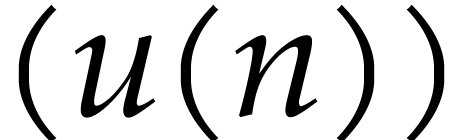 of
of
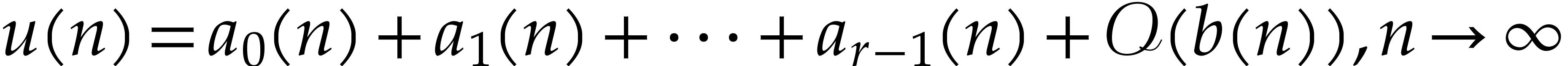 . We will show that solving this equation can
be done in polynomial time in
. We will show that solving this equation can
be done in polynomial time in 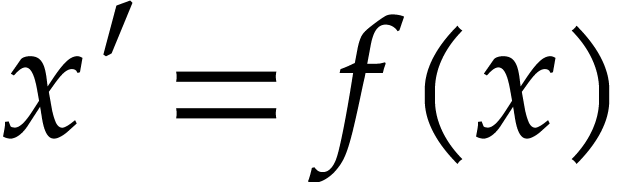 and the genus of
and the genus of
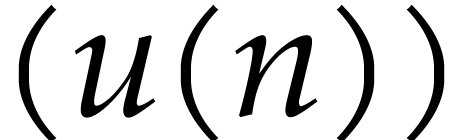 through the use of Riemann-Roch spaces and the
Divisor Class Group of
through the use of Riemann-Roch spaces and the
Divisor Class Group of 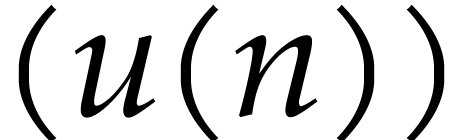 . If the time allows it,
we shall also present an irreducibility test relying on description of
the Brauer group of
. If the time allows it,
we shall also present an irreducibility test relying on description of
the Brauer group of 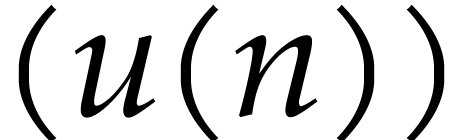 in terms of its local
Brauer groups. The irreducibility test can be done in polynomial time
in
in terms of its local
Brauer groups. The irreducibility test can be done in polynomial time
in 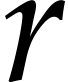 and the genus of
and the genus of 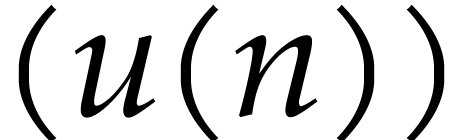 .
.
25 mars 2024
Multigraded Castelnuovo-Mumford regularity and Groebner bases
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Groebner bases (GBs) are the “Swiss Army knife” of
symbolic computations with polynomials. They are a special set of
generators of an ideal which allow us to manipulate extremely
complicated objects, so computing them is an intrinsically hard
problem. To estimate the complexity of such computations, an extended
approach is to bound the maximal degrees of the polynomials appearing
in the GBs. One of the most important results in this direction is due
to Bayer and Stillman, who showed in the 80s that, in generic
coordinates, the maximal degree of an element in a GB of an
homogeneous ideal with respect to the reverse lexicographical order is
determined by the Castelnuovo-Mumford regularity of the ideal —
an algebraic invariant independent of the GB. In this talk, I will
present a generalization of their results for multi-homogeneous
systems and show how the extension of the Castelnuovo-Mumford
regularity to multi-graded ideals relates to the maximal degrees
appearing in the computation of a GB. This talk is based on ongoing
work with
18 mars 2024
An introduction to computer-assisted proofs via a posteriori validation
Heure: from 11h00 to 12h00
Salle: Grace Hopper
The goal of a posteriori validation methods is to get a quantitative and rigorous description of some specific solutions of nonlinear ODEs or PDEs, based on numerical simulations. The general strategy consists in combining a priori and a posteriori error estimates, interval arithmetic, and a fixed point theorem applied to a quasi-Newton operator. Starting from a numerically computed approximate solution, one can then prove the existence of a true solution in a small and explicit neighborhood of the numerical approximation.
I will first present the main ideas behind these techniques on a simple example, and then describe how they can be used for rigorously integrating some differential equations.
11 mars 2024
On rule-based models of dynamical systems
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Chemical reaction networks (CRN) constitute a standard formalism used in systems biology to represent high-level cell processes in terms of low-level molecular interactions. A CRN is a finite set of formal kinetic reaction rules with well-defined hypergraph structure and several possible dynamics. One CRN can be interpreted in a hierarchy of formal semantics related by either approximation or abstraction relationships, including
-
the differential semantics (ordinary differential equation),
-
stochastic semantics (continuous-time Markov chain),
-
probabilistic semantics (probabilistic Petri net forgetting about continuous time),
-
discrete semantics (Petri net forgetting about transition probabilities),
-
Boolean semantics forgetting about molecular numbers,
-
or just the hypergraph structure semantics.
We shall show how these different semantics come with different analysis tools which can reveal various dynamical properties of the other interpretations. In our CRN modeling software BIOCHAM (biochemical abstract machine), these static analysis tools are complemented by dynamic analysis tools based on quantitative temporal logic, and by an original CRN synthesis symbolic computation pipeline for compiling any computable real function in an elementary CRN over a finite set of abstract molecular species.
26 février 2024
Approximate flatness-based control via a case study: Drugs administration in some cancer treatments
Heure: from 11h00 to 12h00
Salle: Grace Hopper
We present some “in silico” experiments to design combined chemo- and immunotherapy treatment schedules. We introduce a new framework by combining flatness-based control, which is a model-based setting, along with model-free control. The flatness property of the used mathematical model yields straightforward reference trajectories. They provide us with the nominal open-loop control inputs. Closing the loop via model-free control allows to deal with the uncertainties on the injected drug doses. Several numerical simulations illustrating different case studies are displayed. We show in particular that the considered health indicators are driven to the safe region, even for critical initial conditions. Furthermore, in some specific cases there is no need to inject chemotherapeutic agents.
Joint work with
8 decembre 2023
Application of differential elimination for physics-based deep learning and computing
Heure: from 14h00 to 15h00
Salle: Darboux amphitheater, Institut Henri Poincaré (11 Rue Pierre et Marie Curie, Paris)
In the field of differential algebra, differential elimination refers to the elimination of specific variables and/or their derivatives from differential equations. One well-known application of differential elimination is in the model identifiability analysis. Recently, there has been a growing demand for further applications in addition to this.
In this talk, we introduce two recent applications in the field related to physics. The first application field is physics-based deep learning. In particular, we introduce the application of differential elimination for Physics-Informed Neural Networks (PINNs), which are types of deep neural networks integrating governing equations behind the data. The second application is about physics-based computing, or, physical computing. This refers to information processing leveraging the dynamics of physical systems such as soft materials and fluids. In this talk, we show the application of differential elimination to time-series information processing via physical computing.
24 avril, 2023
Set-based methods for the analysis of dynamical systems
Heure: from 11h00 to 12h00
Salle: Grace Hopper
In this talk, I will describe some set-based methods (i.e.
«guaranteed» numerical methods) that we developed for
helping analyze and validate dynamical (and control) systems. I will
go through a number of problems, ranging from plain reachability,
reach-avoid, robust reachability to invariance and general temporal
specifications. The robust reachability and general temporal
specifications will introduce the problem of solving some form of
quantifier elimination, for which we will give a simple set-based
method for inner and outer-approximating the set of solutions. Based
on joint works with
17 avril, 2023
Calcul formel et diffusion chaotique des mouvements planétaires dans le système solaire
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
La mise en évidence du mouvement chaotique des planètes dans le système solaire a été obtenu grâce à une intégration des équation modernisées de leur mouvement (Laskar, 1989). Ce système d'équations contenant plus de 150 000 termes avait été obtenu par des méthodes de calcul formel très dédiées, dont l'adaptation n'était pas aisée. depuis 1988 a commencé la construction d'un système de calcul formel général, TRIP, spécialement adapté aux calculs de la mécanique céleste. Nous avons utilisé ce système récemment pour obtenir une meilleure compréhension de l'origine du chaos dans le système solaire, et pour étudier la diffusion chaotique du mouvement des planètes sur des durées bien supérieures à l'âge de l'univers.
27 mars, 2023
Finding exact linear reductions of dynamical models
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Dynamical models described by systems of polynomial differential equations are a fundamental tool in the sciences and engineering. Exact model reduction aims at finding a set of combinations of the original variables which themselves satisfy a self-contained system. There exist algorithmic solutions which are able to rapidly find linear reductions of the lowest dimension under certain additional constraints on the input or output.
In this talk, I will present a general algorithm for finding exact linear reductions. The algorithm finds a maximal chain of reductions by reducing the question to a search for invariant subspaces of matrix algebras. I will describe our implementation and show how it can be applied to models from literature to find reductions which would be missed by the earlier approaches.
This is a joint work with
20 mars, 2023
Using Algebraic Geometry for Solving Differential Equations
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
Given a first order autonomous algebraic ordinary
differential equation, i.e. an equation of the form 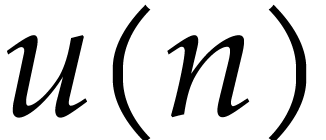 with polynomial F and complex coefficients, we
present a method to compute all formal power series solutions with
fractional exponents. By considering y and y′ as independent
variables, results from Algebraic Geometry can be applied to the
implicitly defined plane curve. This leads to a complete
characterization of initial values with respect to the number of
distinct solutions extending them. Furthermore, the computed formal
solutions are convergent in suitable neighborhoods and for any given
point in the complex plane there exists a solution of the
differential equation which defines an analytic curve
passing through this point. These results can be generalized to
systems of ODEs which implicitly define a space curve and to
local solutions with real coefficients only. This is a joint work
with
with polynomial F and complex coefficients, we
present a method to compute all formal power series solutions with
fractional exponents. By considering y and y′ as independent
variables, results from Algebraic Geometry can be applied to the
implicitly defined plane curve. This leads to a complete
characterization of initial values with respect to the number of
distinct solutions extending them. Furthermore, the computed formal
solutions are convergent in suitable neighborhoods and for any given
point in the complex plane there exists a solution of the
differential equation which defines an analytic curve
passing through this point. These results can be generalized to
systems of ODEs which implicitly define a space curve and to
local solutions with real coefficients only. This is a joint work
with
20 février, 2023
Faster algorithms for symmetric polynomial systems
Heure: from 11h00 to 12h00
Salle: Philippe Flajolet
Many important polynomial systems have additional structure, for example, generating polynomials invariant under the action of the symmetric group. In this talk we consider two problems for such systems. The first focuses on computing the critical points of a polynomial map restricted to an algebraic variety, a problem which appears in many application areas including polynomial optimization. Our second problem is to decide the emptiness of algebraic varieties over real fields, a starting point for many computations in real algebraic geometry. In both cases we provide efficient probabilistic algorithms for which take advantage of the special invariant structure. In particular in both instances our algorithms obtain their efficiency by reducing the computations to ones over the group orbits and make use of tools such as weighted polynomial domains and symbolic homotopy methods.
12 decembre, 2022
Séance organisée dans le cadre du pôle Mathématiques informatiques
Sparse interpolation
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Computer algebra deals with exact computations with mathematical formulas. Often, these formulas are very large and often they can be rewritten as polynomials or rational functions in well chosen variables. Direct computations with such expressions can be very expensive and may lead to a further explosion of the size of intermediate expressions. Another approach is to systematically work with evaluations. For a given problem, like inverting a matrix with polynomial coefficients, evaluations of the solution might be relatively cheap to compute. Sparse interpolation is a device that can then be used to recover the result in symbolic form from sufficiently many evaluations. In our talk, we will survey a few classical and a new approach for sparse interpolation, while mentioning a few links with other subjects.
5 decembre, 2022
Cache complexity in computer algebra
Heure: from 11h00 to 12h00
Salle: Grace Hopper
In the computer algebra literature, optimizing memory usage (e.g. minimizing cache misses) is often considered only at the software implementation stage and not at the algorithm design stage, which can result in missed opportunities, say, with respect to portability or scalability.
In this talk, we will discuss ideas for taking cache complexity, in combination with other complexity measures, at the algorithm design stage. We will start by a review of different memory models (I/O Complexity, cache complexity, etc.). We will then go through illustrative examples considering both multi-core and many-core architectures.
14 novembre, 2022
Analytic combinatorics and partial differential equations
Heure from 11h00 to 12h00
Salle: Grace Hopper
Many combinatorial structures and probabilistic processes lead to generating functions satisfying partial differential equations, and, in some cases, they even satisfy ordinary differential equations (they are D-finite).
In my talk, I will present results from these last 3 years illustrating this principle, and asymptotic consequences of this, on fundamental objects like Pólya urns, Young tableaux with walls, increasing trees, posets…
I will also prove that some cases are differentially algebraic (not D-finite), and possess surprising stretched exponential asymptotics involving exponents which are zeroes of the Airy function. The techniques are essentially extensions of the methods of analytic combinatorics (generating functions and complex analysis), as presented in the eponymous wonderful book of Flajolet and Sedgewick. En passant, I will also present a new algorithm for uniform random generation (the density method), and new universal distributions, establishing the asymptotic fluctuations of the surface of triangular Young tableaux.
This talk is based on joint work with Philippe Marchal and Michael Wallner:
Periodic Pólya urns, the density method, and asymptotics of Young tableaux, Annals of Probability, 2020.
Young tableaux with periodic walls: counting with the density method, FPSAC, 2021.
7 novembre, 2022
Integral Equation Modelling and Deep Learning
Heure: from 11h00 to 12h00
Salle: Gilles Kahn
Considering models with integro-differential equations is motivated by the following reason: on some examples, the introduction of integral equations increases the expressiveness of the models, improves the estimation of parameter values from error-prone measurements, and reduces the size of the intermediate equations.
Reducing the order of derivation of a differential equation can sometimes be achieved by integrating it. An algorithm was designed by the CFHP team for that purpose. However, successfully integrating integro-differential equations is a complex problem. Unfortunately, there are still plenty of differential equations for which the algorithm does not apply. For example, computing an integrating factor might be required.
Rather than integrating the differential equation, we can perform an integral elimination. We are currently working on this technique which also implies some integration problems. To try to overcome these problems, we are also using deep learning techniques with the hope of finding small calculus tips.
24 juin, 2022
Exact nonlinear reductions of dynamical systems
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Dynamical systems of the form  are widely used
in many sciences. Numerical procedures, such as simulation and
parameter estimation do not work efficiently due to the high dimension
of the dynamical systems. We studied exact reductions of the system,
i.e., computing macro-variables that satisfy self-consistent
differential systems. Thanks to the software CLUE, we can reduce the
dimension of polynomial and rational dynamical systems by a linear
change of variables (i.e., macro-variables are linear combinations of
the original variables) preserving some linear quantities from the
original state variables. In this talk we are going to present a new
method to reduce the dimension of these dynamical systems even further
by performing a nonlinear change of variables. We are going to show
how to look for reductions of this type, how to preserve some
information from the original system and how to compute the new
self-consistent system that the new macro-variables satisfy.
are widely used
in many sciences. Numerical procedures, such as simulation and
parameter estimation do not work efficiently due to the high dimension
of the dynamical systems. We studied exact reductions of the system,
i.e., computing macro-variables that satisfy self-consistent
differential systems. Thanks to the software CLUE, we can reduce the
dimension of polynomial and rational dynamical systems by a linear
change of variables (i.e., macro-variables are linear combinations of
the original variables) preserving some linear quantities from the
original state variables. In this talk we are going to present a new
method to reduce the dimension of these dynamical systems even further
by performing a nonlinear change of variables. We are going to show
how to look for reductions of this type, how to preserve some
information from the original system and how to compute the new
self-consistent system that the new macro-variables satisfy.
24 mai, 2022
Séance organisée dans le cadre du pôle Mathématiques informatiques
Asymptotic Expansions with Error Bounds for Solutions of Linear Recurrences
Heure: from 11h00 to 12h00
Salle: Grace Hopper
When a sequence  of real or complex numbers
satisfies a linear recurrence relation with polynomial coefficients,
it is usually routine to determine its asymptotic behavior for large
of real or complex numbers
satisfies a linear recurrence relation with polynomial coefficients,
it is usually routine to determine its asymptotic behavior for large
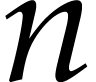 . Well-known algorithms and readily available
implementations are often able, given a recurrence satisfied by
. Well-known algorithms and readily available
implementations are often able, given a recurrence satisfied by  and some additional information on the particular
solution, to compute an explicit asymptotic expansion
and some additional information on the particular
solution, to compute an explicit asymptotic expansion
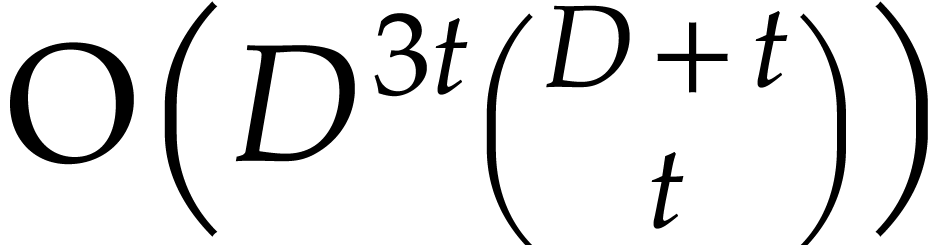
up to any desired order 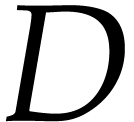 . If, however, one
wishes to prove an inequality satisfied by
. If, however, one
wishes to prove an inequality satisfied by 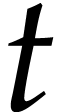 for
all
for
all 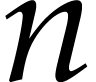 , a big-Oh error term is not sufficient and
an explicit error bound on the difference between the sequence and its
asymptotic approximation is required. In this talk, I will present a
practical algorithm for computing such bounds, under the assumption
that the generating series of the sequence
, a big-Oh error term is not sufficient and
an explicit error bound on the difference between the sequence and its
asymptotic approximation is required. In this talk, I will present a
practical algorithm for computing such bounds, under the assumption
that the generating series of the sequence  is
solution of a differential equation with regular (Fuchsian) dominant
singularities. I will show how it can be used to verify the positivity
of a certain explicit sequence, which T. Yu and J. Chen recently
proved to imply uniqueness of the surface of genus one in
is
solution of a differential equation with regular (Fuchsian) dominant
singularities. I will show how it can be used to verify the positivity
of a certain explicit sequence, which T. Yu and J. Chen recently
proved to imply uniqueness of the surface of genus one in  of minimal bending energy when the isoperimetric ratio
is prescribed.
of minimal bending energy when the isoperimetric ratio
is prescribed.
Based on joint work with Ruiwen Dong and Stephen Melczer.
10 mai, 2022
Platitude généralisée et planification de trajectoire pour des modèles d'avions
Heure: from 11h00 to 12h00
Salle: Grace Hopper
En négligeant les forces exercées par les commandes, un avion est modélisé par un système plat. Dans un premier temps, on utilise un bouclage pour compenser les erreurs de modèle et maintenir la trajectoire du système complet non plat au voisinage de la trajectoire calculée pour l'approximation plate. Dans un second temps, on réinjecte dans les équations les valeurs des commandes fournie par l'approximation plate et on itère le processus, ce qui permet d'obtenir une planification de trajectoire très précise pour le modèle complet. Quelques exemples sont fournis illustrant les possibilités offertes par des packages en Maple.
Cette nouvelle approche est appelée platitude
généralisée. Le paramétrage fourni
dépend d'une infinité de dérivées des
sorties plates, ce qui conforte une conjecture selon laquelle tout
système commandable est plat si on autorise des
paramétrage dépendant d'une infinité de
dérivations. Il est à noter que les conditions
nécessaires de platitude de
19 avril, 2022
Simultaneous Rational Function Reconstruction with Errors: Handling Poles and Multiplicities
Heure: from 11h00 to 12h00
Salle: Grace Hopper
In this talk I focus on an evaluation-interpolation technique for reconstructing a vector of rational functions (with the same denominator), in presence of erroneous evaluations. This problem is also called Simultaneous Rational Function Reconstruction with errors (SRFRwE) and it has significant applications in computer algebra (e.g.for the parallel resolution of polynomial linear systems) and in algebraic coding theory (e.g. for the decoding of the interleaved version of the Reed-Solomon codes). Indeed, an accurate analysis of this problem leads to interesting results in both these scientific domains. Starting from the SRFRwE, we then introduce its multi-precision generalization, in which we include evaluations with certain precisions. Our goal is to reconstruct a vector of rational functions, given, among other information, a certain number of evaluation points. Thus, these evaluation points may be poles of the vector that we want to recover. Our multi-precision generalization also allows us to handle poles with their respective orders. The main goal of this work is to determine a condition on the instance of this SRFRwE problem (and its generalized version) which guarantee the uniqueness of the interpolating vector. This condition is crucial for the applications: in computer algebra it affects the complexity of the corresponding SRFRwE resolution algorithm, while in coding theory, it affects the number of errors that can be corrected. We determine a condition which allows us to correct any errors. Then we exploit and revisit results related to the decoding of interleaved Reed-Solomon codes in order to introduce a better condition for correcting random errors.
14 decembre, 2021
Differential flatness for fractional order dynamic systems
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
Differential flatness is a property of dynamic systems that allows the expression of all the variables of the system by a set of differentially independent functions, called flat output, depending on the variables of the system and their derivatives. The differential flatness property has many applications in automatic control theory, such as trajectory planning and trajectory tracking. This property was first introduced for the class of integer order systems and then extended to the class of fractional order systems. This talk will present the flatness of the fractional order linear systems and more specifically the methods for computing fractional flat outputs.
7 decembre, 2021
msolve: a library for solving multivariate polynomial systems
Heure: from 11h00 to 12h00
Salle: Grace Hopper
In this talk, we present a new open source library, developed with J.
This talk will cover a short presentation of the current
functionalities provided by msolve, followed by an overview of the
implemented algorithms which will motivate the design choices
underlying the library. We will also compare the practical
performances of msolve with leading computer algebra systems such as
Magma, Maple, Singular, showing that msolve can tackle systems which
were out of reach by the computer algebra software state-of-the-art.
If time permits, we will report on new algorithmic developments for
ideal theoretic operations (joint work with J.
19 octobre, 2021
Reconciling discrete and continuous modeling for the analysis of large-scale Markov chains
Heure: from 11h00 to 12h00
Salle: Grace Hopper
Markov chains are a fundamental tool for stochastic modeling across a wide range of disciplines. Unfortunately, their exact analysis is often hindered in practice due to the massive size of the state space - an infamous problem plaguing many models based on a discrete state representation. When the system under study can be conveniently described as a population process, approximations based on mean-field theory have proved remarkably effective. However, since such approximations essentially disregard the effect of noise, they may potentially lead to inaccurate estimations under conditions such as bursty behavior, separation of populations into low- and high-abundance classes, and multi-stability. This talk will present a new analytical method that combines an accurate discrete representation of a subset of the state space with mean-field equations to improve accuracy at a user-tunable computational cost. Challenging examples drawn from queuing theory and systems biology will show how the method significantly outperforms state-of-the-art approximation methods.
This is joint work with Luca Bortolussi, Francesca Randone, Andrea Vandin, and Tabea Waizmann.
5 octobre, 2021
Linear PDE with constant coefficients
Heure: from 11h00 to 12h00
Salle: Henri Poincaré
I will present a work about practical methods for computing the space
of solutions to a system of linear PDE with constant coefficients.
These methods are based on the Fundamental Principle of
Ehrenpreis–Palamodov from the 1960s which assert that every
solution can be written as finite sum of integrals over some algebraic
varieties. I will first present the main historical results and then
recent algorithm for computing the space of solutions.
This is a
joint work with Marc Harkonen and Bernd Sturmfels.
28 septembre, 2021
DD-finite functions: a computable extension for holonomic functions
Heure: from 11h00 to 12h00
Salle: Grace Hopper
D-finite or holonomic functions are solutions to linear differential equations with polynomial coefficients. It is this property that allow us to exactly represent these functions on the computer. in this talk we present a natural extension of this class of functions: the DD-finite functions. These functions are the solutions of linear differential equations with D-finite coefficients. We will see the properties these functions have and how we can algorithmically compute with them.
7 juin 2021
Réduction des intégrales premières des champs de vecteurs du plan
Heure: from 14h00 to 15h00
Exposé en ligne
Les intégrales premières symboliques d'un champ de vecteur rationnel du plan sont de 4 types: rationnelles, darbouxiennes, liouvilliennes et de Riccati. Il est possible de les rechercher jusqu'à un certain degré, mais en trouver une ne signifie pas qu'il n'en existe pas d'autres plus simples mais de degré plus élevé. Le problème de Poincaré consiste à trouver les intégrales premières rationnelles d'un tel champ de vecteur. Nous y ajouterons l'hypothèse qu'une intégrale première symbolique est donnée d'avance, et il nous « suffira » ainsi de savoir si l'on peut la simplifier. Nous présenterons des algorithmes de simplification d'intégrales premières pour le cas Ricatti et liouvilien, et nous verrons, qu'à l'exception d'un cas particulier, cela est aussi possible pour le cas darbouxien. Nous détaillerons un exemple résistant et ses liens avec les courbes elliptiques.
10 mai 2021
Algèbre différentielle et géométrie différentielle tropicale
Heure: from 14h00 to 15h00
Exposé en ligne
Dans cet exposé, je ferai un lien entre l'algèbre différentielle de Ritt et Kolchin et la géométrie différentielle tropicale initiée par Grigoriev, sur la question de l'existence de solutions en séries entières formelles. Sur la fin de l'exposé, je m'attarderai sur un théorème d'approximation qui constitue la partie difficile du théorème fondamental de la géométrie différentielle tropicale.
12 avril 2021
Sparse Interpolation in terms of multivariate Chebyshev polynomials
Heure: from 15h00 to 16h00
Exposé en ligne: https://greenlight.lal.cloud.math.cnrs.fr/b/oll-ehe-mn3
Sparse interpolation refers to the exact recovery of a function as a short linear combination of basis functions from a limited number of evaluations. For multivariate functions, the case of the monomial basis is well studied, as is now the basis of exponential functions. Beyond the multivariate Chebyshev polynomial obtained as tensor products of univariate Chebyshev polynomials, the theory of root systems allows to define a variety of generalized multivariate Chebyshev polynomials that have connections to topics such as Fourier analysis and representations of Lie algebras. We present a deterministic algorithm to recover a function that is the linear combination of at most r such polynomials from the knowledge of r and an explicitly bounded number of evaluations of this function.
This is a joint work with Michael Singer (https://hal.inria.fr/hal-02454589v1).
29 mars, 2021
Gröbner technology over free associative algebras over rings: semi-decidability, implementation and applications
Heure: from 14h00 to 15h00
Exposé en ligne: https://webconf.math.cnrs.fr/b/pog-m6h-mec
Computations with finitely presented associative algebras traditionally boil down to computations over free associative algebras. In particular, there is a notion of Gröbner(–Shirshov) basis, but generally its computation does not terminate, and thus the ideal membership problem is not solvable. However, many important special cases can be approached.
The Letterplace correspondence for free algebras, introduced by La Scala and Levandovskyy, allows to reformulate the Gröbner theory and to use highly tuned commutative data structures in the implementation and to reuse parts of existing algorithms in the free non-commutative situation. We report on the newest official release of the subsystem of Singular called Letterplace. With it, we offer an unprecedented functionality, some of which for the first time in the history of computer algebra. In particular, we present practical tools for elimination theory (via truncated Gröbner bases and via supporting several kinds of elimination orderings), dimension theory (Gel'fand-Kirillov and global homological dimension), and for further homological algebra (such as syzygy bimodules and lifts for ideals and bimodules) to name a few.
Another activity resulted in the extension of non-commutative
Gröbner bases for supporting the coefficients in principal ideal
rings including 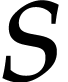 . Such computations are of big
value (for example, in representation theory), since the results can
be treated as universal for fields of arbitrary characteristic. Quite
nontrivial examples illustrate the powerful abilities of the system we
have developed and open the way for new applications.
. Such computations are of big
value (for example, in representation theory), since the results can
be treated as universal for fields of arbitrary characteristic. Quite
nontrivial examples illustrate the powerful abilities of the system we
have developed and open the way for new applications.
22 mars 2021
Fast algorithm and sharp degree bounds for one block quantifier elimination over the reals
Heure: from 14h00 to 15h00
Exposé en ligne
Quantifier elimination over the reals is one of the most important algorithmic problem in effective real algebraic geometry. It finds applications in several areas of computing and engineering sciences such as program verification, computational geometry, robotics and biology to cite a few. Geometrically, eliminating one block of quantifiers consists in computing a semi-algebraic formula which defines the projection of the set defined by the input polynomial constraints on the remaining set of variables (which we call parameters).
In this work, we design a fast algorithm computing a semi-algebraic
formula defining a dense subset in the interior of that projection
when the input is composed of a polynomial system of equations. Using
the theory of Groebner bases, we prove that, on generic
inputs, its complexity is  where
where 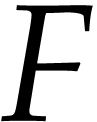 is the maximum degree in the output formulas and
is the maximum degree in the output formulas and 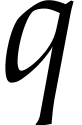 is the number of parameters. We provide a new
explicit bound on
is the number of parameters. We provide a new
explicit bound on 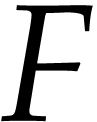 which improves the
state-of-the-art and make explicit the determinantal nature of these
formulas which make them easier to evaluate than the formulas
delivered by the previous algorithms. Our implementation shows the
practical efficiency of our approach as it allows us to tackle
examples which are out of reach of the state-of-the-art software.
which improves the
state-of-the-art and make explicit the determinantal nature of these
formulas which make them easier to evaluate than the formulas
delivered by the previous algorithms. Our implementation shows the
practical efficiency of our approach as it allows us to tackle
examples which are out of reach of the state-of-the-art software.
This is joint work with
8 mars 2021
Surreal numbers with exponential and omega-exponentiation
Heure: from 13h00 to 14h00
Exposé en ligne
Surreal numbers have been introduced by Conway while working on game theory: they allow to evaluate partial combinatorial games of any size! This is so because they consist in a proper class containing “all numbers great and small”, but also due to the richness of the structure we can endow them with: an ordered real closed field. Moreover, surreal numbers can be seen as formal power series with exp, log and derivation. This turns them into an important object also in model theory (universal domain for many theories) and real analytic geometry (formal counterpart for non oscillating germs of real functions).
In this talk, I will introduce these fascinating objects, starting with the very basic definitions, and will give a quick overview, with a particular emphasis on exp (which extends exp on the real numbers) and the omega map (which extends the omega-exponentiation for ordinals). This will help me to subsequently present our recent contributions with A. Berarducci, S. Kuhlmann and V. Mantova concerning the notion of omega-fields (possibly with exp). One of our motivations is to clarify the link between composition and derivation for surreal numbers.
22 février 2021
Primary ideals and differential operators
Heure: from 14h00 to 15h00
Exposé en ligne
The main objective will be to describe primary ideals with the use of differential operators. These descriptions involve the study of several objects of different nature, so to say; the list includes: differential operators, differential equations with constant coefficients, Macaulay's inverse systems, symbolic powers, Hilbert schemes, and the join construction.
As an interesting consequence, we will introduce a new notion of differential powers which coincides with symbolic powers in many interesting non-smooth settings, and so it could serve as a generalization of the Zariski-Nagata Theorem. I will report on some joint work with Roser Homs and Bernd Sturmfels.
1er décembre 2020
Algebraic geometry codes from surfaces over finite fields
Heure : from 15h00 to 16h00
Exposé en ligne
Let 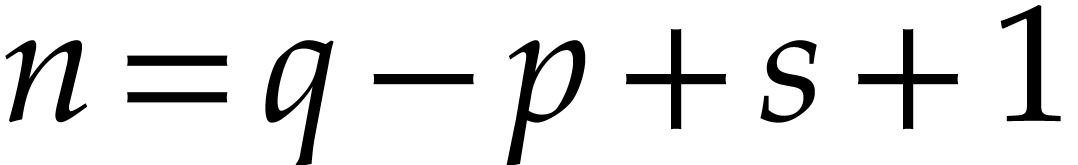 be a polynomial ring in
be a polynomial ring in 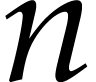 variables with coefficients in a field
variables with coefficients in a field 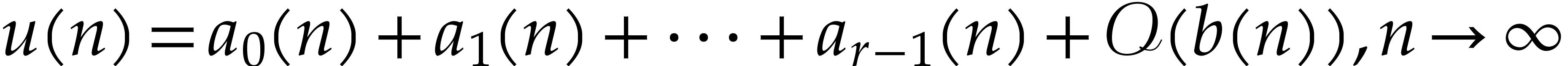 of
characteristic zero. Consider a sequence of
of
characteristic zero. Consider a sequence of 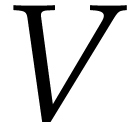 polynomials
polynomials 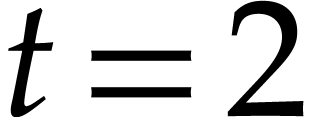 in
in 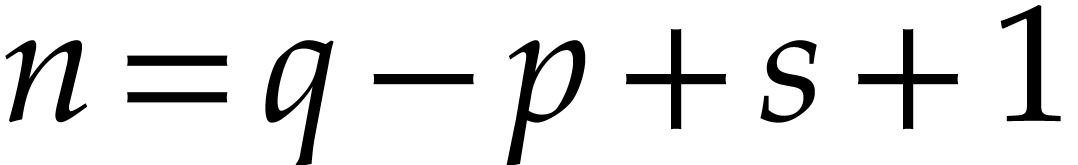 and a
polynomial matrix
and a
polynomial matrix 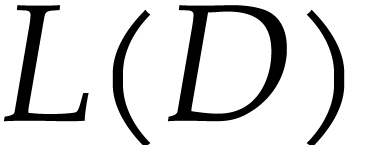 in
in 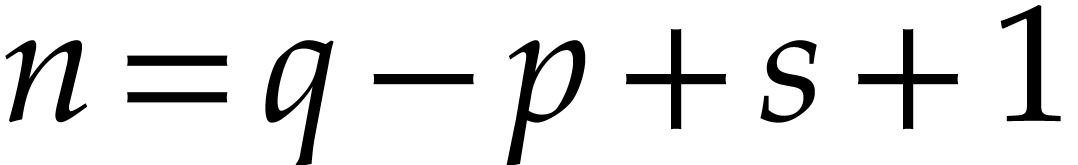 with
with 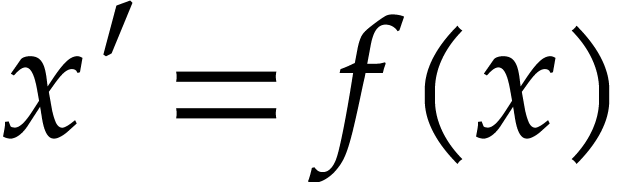 rows and
rows and 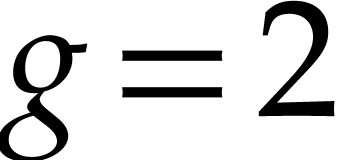 columns
such that
columns
such that 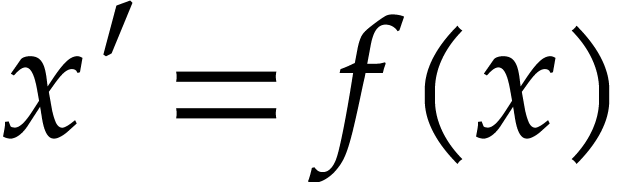 is at most
is at most 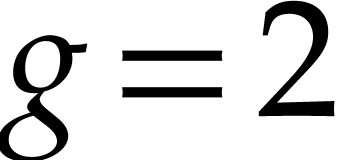 and
and  . We are interested in the algebraic set
. We are interested in the algebraic set
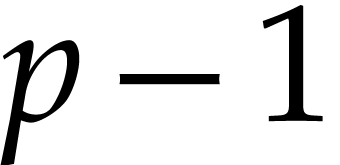 of point in an algebraic closure of
of point in an algebraic closure of 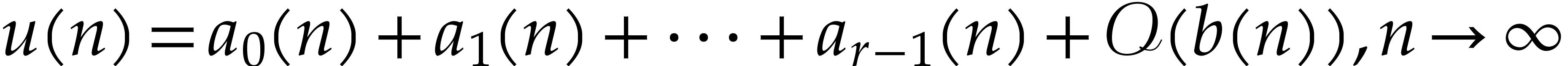 at which all polynomials in
at which all polynomials in 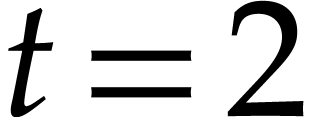 and
all
and
all 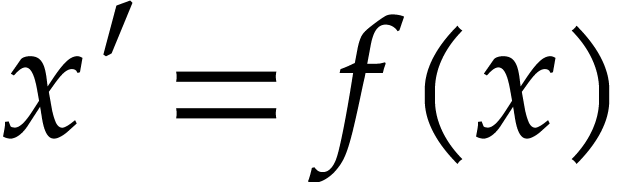 -minors of
-minors of 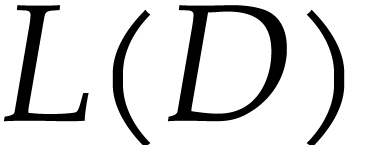 vanish.
Such polynomial systems arise in a variety of applications including
for example polynomial optimization and computational geometry.
vanish.
Such polynomial systems arise in a variety of applications including
for example polynomial optimization and computational geometry.
We investigate the structures of 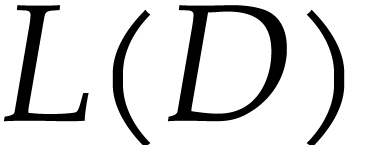 to provide
bounds on the number of isolated points in
to provide
bounds on the number of isolated points in 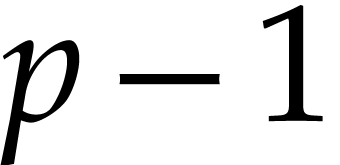 depending on the maxima of the degrees in rows (resp.
columns) of
depending on the maxima of the degrees in rows (resp.
columns) of 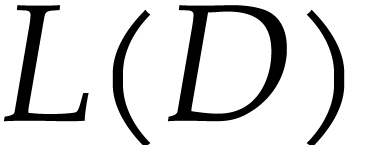 or the mixed volumes of column
supports of
or the mixed volumes of column
supports of 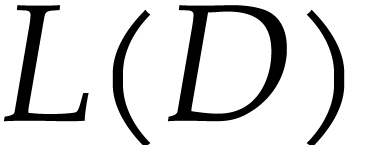 when we study the total degrees of
all polynomials
when we study the total degrees of
all polynomials 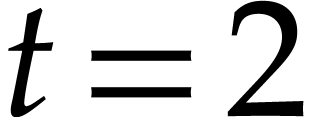 and all entries of
and all entries of 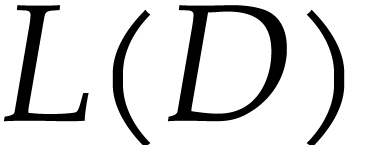 or when these polynomials are sparse. In addition, we
design probabilistic homotopy algorithms for computing the isolated
points with our algorithms running in time that is polynomial in the
bound on the number of isolated points. We also derive complexity
bounds for the particular but important case where
or when these polynomials are sparse. In addition, we
design probabilistic homotopy algorithms for computing the isolated
points with our algorithms running in time that is polynomial in the
bound on the number of isolated points. We also derive complexity
bounds for the particular but important case where 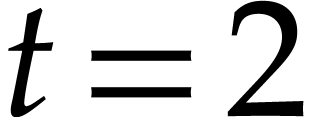 and the columns of
and the columns of 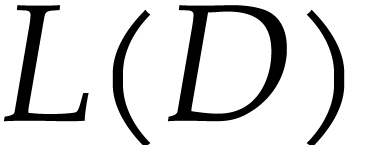 satisfy weighted degree
constraints. Such systems arise naturally in the computation of
critical points of maps restricted to algebraic sets when both are
invariant by the action of the symmetric group.
satisfy weighted degree
constraints. Such systems arise naturally in the computation of
critical points of maps restricted to algebraic sets when both are
invariant by the action of the symmetric group.
This is joint work with J.-C. Faugère, J. D. Hauenstein, G. Labahn, M. Safey El Din and É. Schost.
24 novembre 2020
Degroebnerization and error correcting codes: Half Error Locator
Polynomial
Heure : de 15h00 à 16h00
Exposé en ligne
The concept of “Degroebnerization” has been introduced by Mora within his books on the bases of previous results by Mourrain, Lundqvist, Rouiller.
Since the computation of Gröbner bases is inefficient and
sometimes unfeasible, the Degroebnerization proposes to limit their
use to the cases in which it is really necessary, finding other tools
to solve problems that are classically solved by means of Gröbner
bases. We propose an example of such problems, dealing with efficient
decoding of binary cyclic codes by means of the locator polynomial.
Such a polynomial has variables corresponding to the syndromes, as
well as variables each corresponding to each error location. Decoding
consists then in evaluating the polynomial at the syndromes and
finding the roots in the corresponding variable. It is necessary to
look for a sparse polynomial, so that the evaluation is not too
inefficient. In this talk we show a preliminary result in this
framework; a polynomial of this kind can be found—for error
correction capability 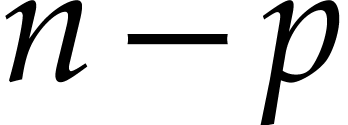 —in a
degroebnerized fashion, and it has linear growth on the length of the
code. We will also give some hints on potential extensions to more
general codes.
—in a
degroebnerized fashion, and it has linear growth on the length of the
code. We will also give some hints on potential extensions to more
general codes.
27 octobre 2020
Algebraic geometry codes from surfaces over finite fields
Heure : de 14h00 à 15h00, Salle : Grace Hopper
Retransmission en ligne : https://webconf.math.cnrs.fr/b/pog-4rz-uec
Algebraic geometry codes were introduced by Goppa in 1981 on curves defined over finite fields and were extensively studied since then. Even though Goppa construction holds on varieties of dimension higher than one, the literature is less abundant in this context. However, some work has been undertaken in this direction, especially on codes from surfaces. The goal of this talk is to provide a theoretical study of algebraic geometry codes constructed from surfaces defined over finite fields, using tools from intersection theory. First, we give lower bounds for the minimum distance of these codes in two wide families of surfaces: those with strictly-nef or anti-nef canonical divisor, and those which do not contain absolutely irreducible curves of small genus. Secondly, we specialize and improve these bounds for particular families of surfaces, for instance in the case of abelian surfaces and minimal fibrations, using the geometry of these surfaces.
The results appear in two joint works with Y. Aubry, F. Herbaut and M. Perret, preprints: https://arxiv.org/pdf/1904.08227.pdf and https://arxiv.org/abs/1912.07450.
13 obtobre 2020
A new algorithm for finding the input-output equations of differential models
(Travail en commun avec Christian Goodbreak, Heather Harrington, and Gleb Pogudin)
Heure : de 14h00 à 15h00, Salle : Gilles Kahn
The input-output equations of a differential model are consequences of the differential model which are also “minimal” equations depending only on the input, output, and parameter variables. One of their most important applications is the assessment of structural identifiability.
In this talk, we present a new resultant-based method to compute the input-output equations of a differential model with a single output. Our implementation showed favorable performance on several models that are out of reach for the state-of-the-art software. We will talk about ideas and optimizations used in our method as well as possible ways to generalize them.
7 juillet 2020
Computing Riemann–Roch spaces in subquadatric time
(Travail en commun avec A. Couvreur et G. Lecerf)
Heure : de 14h00 à 15h00, Salle : téléconference
Given a divisor 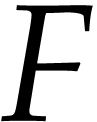 (i.e. a formal sum of points
on a curve), the Riemann–Roch space
(i.e. a formal sum of points
on a curve), the Riemann–Roch space  is
the set of rational functions whose poles and zeros are constrained by
is
the set of rational functions whose poles and zeros are constrained by
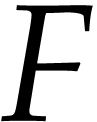 . These spaces are important objects in
algebraic geometry and computing them explicitly has applications in
various fields: diophantine equations, symbolic integration,
arithmetic in Jacobians of curves and error-correcting codes.
. These spaces are important objects in
algebraic geometry and computing them explicitly has applications in
various fields: diophantine equations, symbolic integration,
arithmetic in Jacobians of curves and error-correcting codes.
Since the 1980's, many algorithms were designed to compute Riemann–Roch paces, incorporating more and more efficient primitives from computer algebra. The state-of-the-art approach ultimately reduces the problem to linear algebra on matrices of size comparable to the input.
In this talk, we will see how one can replace linear algebra by structured linear algebra on polynomial matrices of smaller size. Using a complexity bound due to Neiger, we design the first subquadratic algorithm for computing Riemann–Roch spaces.
23 juin 2020
Exact model reduction by constrained linear lumping
(Travail en commun avec A. Ovchinnikov, I.C. Perez Verona, et M. Tribastone)
Heure : de 14h00 à 15h00, Salle : téléconference
We solve the following problem: given a system of ODEs with polynomial right-hand side, find the maximal exact model order reduction by a linear transformation that preserves the dynamics of user-specified linear combinations of the original variables. Such transformation can reduce the dimension of a model dramatically and lead to new insights about the model. We will present an algorithm for solving the problem and applications of the algorithm to examples from literature. Then I will describe directions for further research and their connections with the structure theory of finite-dimensional algebras.
9 juin 2020
Asymptotic differential algebra
Heure : de 14h00 à 15h00, Salle : téléconference
I will describe a research program put forward by Joris van der Hoeven and his frequent co-authors Lou van den Dries and Matthias Aschenbrenner, in the framework of asymptotic differential algebra. This program sets out to use formal tools (log-exp transseries) and number theoretic / set-theoretic tools (surreal numbers) to select and study properties of “monotonically regular” real-valued functions.
26 mai 2020
Counting points on hyperelliptic curves defined over finite fields
of large characteristic: algorithms and complexity
Heure : de 14h00 à 15h00, Salle : téléconference
Counting points on algebraic curves has drawn a lot of attention due
to its many applications from number theory and arithmetic geometry to
cryptography and coding theory. In this talk, we focus on counting
points on hyperelliptic curves over finite fields of large
characteristic 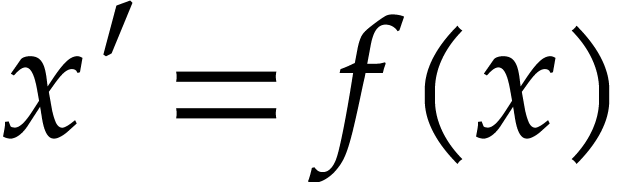 . In this setting, the most
suitable algorithms are currently those of Schoof and Pila, because
their complexities are polynomial in
. In this setting, the most
suitable algorithms are currently those of Schoof and Pila, because
their complexities are polynomial in 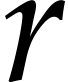 . However,
their dependency in the genus
. However,
their dependency in the genus 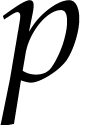 of the curve is
exponential, and this is already a problem even for
of the curve is
exponential, and this is already a problem even for  .
.
Our contributions mainly consist of establishing new complexity bounds
with a smaller dependency in 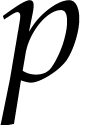 of the exponent
of
of the exponent
of 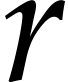 . For hyperelliptic curves, previous work
showed that it was quasi-quadratic, and we reduced it to a linear
dependency. Restricting to more special families of hyperelliptic
curves with explicit real multiplication (RM), we obtained a constant
bound for this exponent.
. For hyperelliptic curves, previous work
showed that it was quasi-quadratic, and we reduced it to a linear
dependency. Restricting to more special families of hyperelliptic
curves with explicit real multiplication (RM), we obtained a constant
bound for this exponent.
In genus 3, we proposed an algorithm based on those of Schoof and Gaudry–Harley–Schost whose complexity is prohibitive in general, but turns out to be reasonable when the input curves have explicit RM. In this more favorable case, we were able to count points on a hyperelliptic curve defined over a 64-bit prime field.
In this talk, we will carefully reduce the problem of counting points to that of solving polynomial systems. More precisely, we will see how our results are obtained by considering either smaller or structured systems and choosing a convenient method to solve them.
12 mai 2020
Shortest paths… from Königsberg to the tropics
Heure : de 14h00 à 15h00, Salle : téléconference
Trying to avoid technicalities, we underline the contribution of
Jacobi to graph theory and shortest paths problems. His starting point
is the computation of a maximal transversal sum in a square 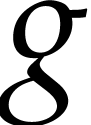 matrix, that is choosing
matrix, that is choosing 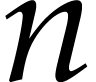 terms
in each row and each column. This corresponds to the tropical
determinant, which was so discovered in Königsberg, on the shores
of the Baltic.
terms
in each row and each column. This corresponds to the tropical
determinant, which was so discovered in Königsberg, on the shores
of the Baltic.
The key ingredient of Jacobi's algorithm for computing the tropical determinant is to build paths between some rows of the matrix, until all rows are connected, which allows to compute a canon, that is a matrix where one can find maximal terms in their columns, located in all different rows, by adding the same constant to all the terms of the same row.
Jacobi gave two algorithms to compute the minimal canon, the first when one already knows a canon, the second when one knows the terms of a maximal transversal sum. They both correspond to well known algorithms for computing shortest paths, the Dijkstra algorithm, for positive weights on the edges of the graph, and the Bellman–Ford algorithm, when some weights can be negative.
After a short tour with Euler over the bridges of Königsberg, a reverence to Kőnig's, Egerváry's and Kuhn's contributions, we will conclude with the computation of a differential resolvent.
28 avril 2020
Interval Summation of Differentially Finite Series
Heure : de 14h00 à 15h00, Salle : téléconférence
I will discuss the computation of rigorous enclosures of sums of power series solutions of linear differential equations with polynomial coefficients ("differentially finite series"). The coefficients of these series satisfy simple recurrences, leading to a simple and fast iterative algorithm for computing the partial sums. When however the initial values (and possibly the evaluation point and the coefficients of the equation) are given by intervals, naively running this algorithm in interval arithmetic leads to an overestimation that grows exponentially with the number of terms. I will present a simple (but seemingly new!) variant of the algorithm that avoids interval blow-up. I will also briefly talk about other aspects of the evaluation of sums of differentially finite series and a few applications.
7 avril 2020
Identifiability from multiple experiments
(Travail en commun avec A. Ovchinnikov, A. Pillay, et T. Scanlon)
Heure : de 14h00 à 15h00, Salle : téléconférence
For a system of parametric ODEs, the identifiability problem is to find which functions of the parameters can be recovered from the input-output data of a solution assuming continuous noise-free measurements.
If one allows to use several generic solutions for the same set of parameter values, it is natural to expect that more functions become identifiable. Natural questions in this case are: which function become identifiable given that enough experiments are performed and how many experiments would be enough? In this talk, I will describe recent results on these two questions.
10 mars 2020
Calcul des sorties linéarisantes d'un système plat
(Travail en commun avec Jean Lévine (Mines de Paris) et Jeremy Kaminski (Holon Institute of Technology)
Heure : de 14h à 15h, Salle : Flajolet
Un système plat est un système différentiel
ordinaire de dimension différentielle positive, donc pourvu de
« commandes » pour l'automaticien, dont les solutions sont
paramétrables sur un ouvert dense par la donnée de 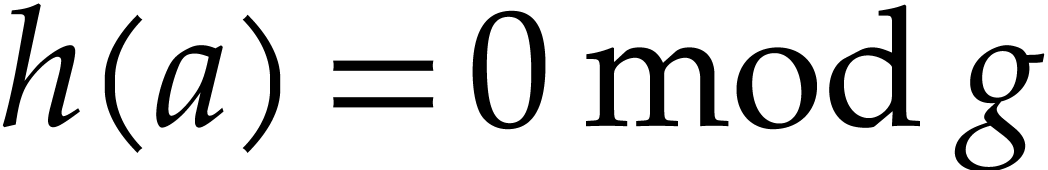 fonctions arbitraires, appelées «
sorties linéarisantes ». Le complémentaire de cet
ouvert correspond aux singularités au sens de la platitude. Il
existe aussi des points pour lesquels les paramétrages
classiques dans la littérature sont singuliers, mais qui sont
des « singularités apparentes »,
c'est-à-dire qu'il existe à leur voisinage un autre
paramétrage qui est, lui, régulier.
fonctions arbitraires, appelées «
sorties linéarisantes ». Le complémentaire de cet
ouvert correspond aux singularités au sens de la platitude. Il
existe aussi des points pour lesquels les paramétrages
classiques dans la littérature sont singuliers, mais qui sont
des « singularités apparentes »,
c'est-à-dire qu'il existe à leur voisinage un autre
paramétrage qui est, lui, régulier.
On donne un aperçu des méthodes disponibles pour calculer les sorties linéarisantes d'un système plat, en s'intéressant particulièrement au cas des singularités apparentes : comment trouver, s'il existe, un paramétrage régulier alternatif. On s'appuiera à titre d'exemple sur des modèles de quadricoptères et d'avions.
18 novembre 2019
Une preuve élémentaire de l'inégalité de Bézout de Heintz
Heure : de 14h à 16h, Salle : Grace Hopper
À l'occasion de la rédaction d'un texte sur l'algorithme « Kronecker » accessible à une large audience, nous avons été amenés à écrire une preuve complète de l'inégalité de Bézout de Heintz pour les variétés algébriques avec des arguments mathématiques disons élémentaires. Dans le même temps nous fournissons une extension de cette inégalité pour les ensembles constructibles, ainsi que quelques applications nouvelles à certains problèmes algorithmiques. Cet exposé présentera les grandes lignes de ces preuves élémentaires. Les applications, vers la fin de l'exposé, seront liées a quelques idées nouvelles autour des ensembles questeurs ("correct test sequences") pour les systèmes d'équations polynomiales.
24 juin 2019
How to get an efficient yet verified arbitrary-precision integer library
(Travail en commun avec Guillaume
Heure : 14h, Salle : Grace Hopper
We present a fully verified arbitrary-precision integer arithmetic library designed using the Why3 program verifier. It is intended as a verified replacement for the mpn layer of the state-of-the-art GNU Multi-Precision library (GMP).
The formal verification is done using a mix of automated provers and user-provided proof annotations. We have verified the GMP algorithms for addition, subtraction, multiplication (schoolbook and Toom-2/2.5), schoolbook division, and divide-and-conquer square root. The rest of the mpn API is work in progress. The main challenge is to preserve and verify all the GMP algorithmic tricks in order to get good performance.
Our algorithms are implemented as WhyML functions. We use a dedicated memory model to write them in an imperative style very close to the C language. Such functions can then be extracted straightforwardly to efficient C code. For medium-sized integers (less than 1000 bits, or 100,000 for multiplication), the resulting library is performance-competitive with the generic, pure-C configuration of GMP.
3 juin 2019
On singularities of flat affine systems with 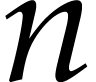 states and
states and 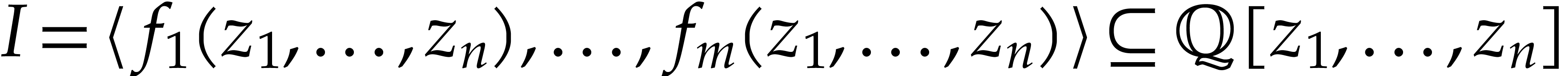 controls
controls
(Travail en commun avec Jean
Heure : 11h, Salle : Grace Hopper
We study the set of intrinsic singularities of flat affine systems
with 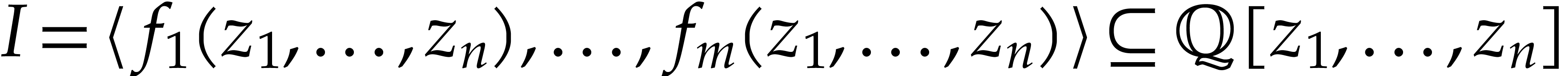 controls and
controls and 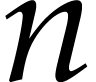 states using the notion of Lie-Bäcklund atlas, previously
introduced by the authors. For this purpose, we prove two easily
computable sufficient conditions to construct flat outputs as a set of
independent first integrals of distributions of vector fields, the
first one in a generic case, namely in a neighborhood of a point where
the
states using the notion of Lie-Bäcklund atlas, previously
introduced by the authors. For this purpose, we prove two easily
computable sufficient conditions to construct flat outputs as a set of
independent first integrals of distributions of vector fields, the
first one in a generic case, namely in a neighborhood of a point where
the 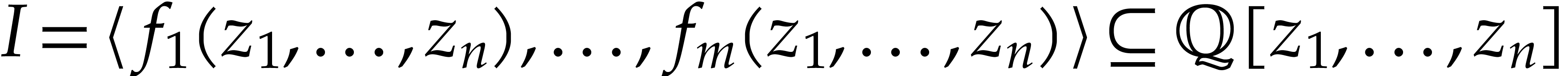 control vector fields are independent, and
the second one at a degenerate point where
control vector fields are independent, and
the second one at a degenerate point where 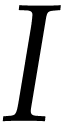 control vector fields are dependent of the
control vector fields are dependent of the 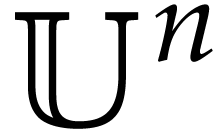 others, with
others, with  . We show that the set of
intrinsic singularities includes the set of points where the system
does not satisfy the strong accessibility rank condition and is
included in the set where the distribution of vector fields,
introduced in the generic case, is singular. We conclude this analysis
by three examples of apparent singularites of flat systems in generic
and non generic degenerate cases.
. We show that the set of
intrinsic singularities includes the set of points where the system
does not satisfy the strong accessibility rank condition and is
included in the set where the distribution of vector fields,
introduced in the generic case, is singular. We conclude this analysis
by three examples of apparent singularites of flat systems in generic
and non generic degenerate cases.
27 mai 2019
Heure : 10h00–12h30, Salle : Gilles Kahn
Séminaire commun avec l'équipe
-
Éric Goubault (École polytechnique, LIX) : Finding Positive Invariants of Polynomial Dynamical Systems – some experiments.Synthetising positive invariants of non-linear ODEs, switched systems or even hybrid systems is a hard problem that has many applications, from control to verification. In this talk, I will present two « exercices de style » for dealing with it, revisiting the classical Lyapunov function approach. The first one is based on algebraic properties of polynomial differential systems (Darboux polynomials, when they exist), for finding polynomial, rational or even some log extensions to rational functions whose level sets or sub-level sets describe positive invariants of these systems, or provide interesting « change of bases » for describing their solutions. The second one is based on topological properties (Wazewski property, mostly) which ensure the existence, in some region of the state space, of a non-empty maximal invariant set. The interest is that there is then in general no need to find complicated functions for precisely describing the invariant set itself, instead we rather use simple template shapes in which a possibly very complicated invariant set lies. The topological criterion can be ensured by suitable SoS relaxations, for polynomial differential systems, that can be implemented using LMI solvers.
-
François Ollivier (CNRS, LIX) : Quelques aspects des méthodes algébriques pour le contrôle et la modélisation.Des notions de base en automatique, comme la contrôlabilité ou l'observabilité sont de nature intrinsèquement algébrique et peuvent être testées par le calcul symbolique. L'algèbre différentielle offre un cadre théorique utile qui permet de ramener de nombreux problèmes à des inclusions de corps différentiels, susceptibles d'être testées par des calculs d'ensembles caractéristiques pour des ordres éliminant certaines variables. C'est le cas de l'identifiabilité. La platitude est une notion plus complexe, efficace pour la planification de trajectoire, mais pour laquelle on ne dispose que de critères spécifiques à des cas particuliers.
L'élimination différentielle se heurte au problème de la complexité des calculs, avec une croissance exponentielle du nombre de monômes avec le degré. Ceci motive la recherche de méthodes permettant de borner a priori l'ordre des calculs utiles, pour lesquelles la borne de Ritt, et celle plus fine de Jacobi, joue un rôle comparable à la borne de Bézout pour l'élimination algébrique.
La borne de Jacobi, conjecturale dans le cas général, peut être prouvée dans le cas quasi régulier. La méthode consiste à se ramener au cas linéaire en considérant le système linéarisé tangent. Celui-ci peut aussi être intégré pour obtenir, numériquement ou formellement, la dépendance des solutions d'un système par rapport à ses paramètres ou ses conditions initiales.
-
Goran Frehse (ENSTA ParisTech, U2IS) : Reachability of Hybrid Systems in High Dimensions.Hybrid systems describe the evolution of a set of real-valued variables over time with ordinary differential equations and event-triggered resets. Numerical methods are widely used to compute trajectories of such systems, which are then used to test them and refine their design. Set-based reachability analysis is a natural extension of this technique form numbers to sets. It is a useful method to formally verify safety and bounded liveness properties of such systems. Starting from a given set of initial states, the successor states are computed iteratively until the entire reachable state space is exhausted. While reachability is undecidable in general and even one-step successor computations are hard to compute, recent progress in approximative set computations allows one to fine-tune the trade-off between computational cost and accuracy. In this talk we present some of the techniques with which systems with complex dynamics and hundreds of variables have been successfully verified.
-
Joris van der Hoeven (CNRS, LIX) : Résolution certifiée d'équations différentielles.Il existe différentes approches pour l'intégration numérique certifiée d'équations différentielles comme les modèles de Taylor et des adaptations de méthodes de Runge–Kutta. Dans notre exposé, nous comparerons les avantages et inconvénients de ces méthodes du point de vue de la complexité pratique et asymptotique.
13 mai 2019
Global identifiability of differential models
Heure : 10h30, Salle : Grace Hopper
Many important real-world processes are modeled using systems of ordinary differential equations (ODEs) involving unknown parameters. The values of these parameters are usually inferred from experimental data. However, due to the structure of the model, there might be multiple parameter values that yield the same observed behavior even in the case of continuous noise-free data. It is important to detect such situations a priori, before collecting actual data. In this case, the only input is the model itself, so it is natural to tackle this question by methods of symbolic computation.
In this talk, I will present our new theoretical results on this problem and new reliable algorithms based on these results that can tackle problems that could not be tackled before, and software SIAN implementing the algorithms. This is a joint work with H. Hong, A. Ovchinnikov, and C. Yap.
6 mars 2019
Fast computation of isomorphisms between finite fields using
elliptic curves
Heure : 14h, Salle : Grace Hopper
Every finite field has prime power cardinality, for every prime power there is a finite field of that cardinality and every two finite fields of the same cardinality are isomorphic. This well known fact poses an algorithmic problem: compute an isomorphism between two explicitly presented finite fields of the same cardinality. We present a randomized algorithm to compute isomorphisms between finite fields using elliptic curves. Prior to this work, the best known run time dependence on the extension degree was quadratic. Our run time dependence is at worst quadratic but is subquadratic if the extension degree has no large prime factor. In particular, the extension degree for which our run time is nearly linear have natural density at least 3/10. The crux of our approach is finding a point on an elliptic curve of a prescribed prime power order or equivalently finding preimages under the Lang map on elliptic curves over finite fields. We formulate this as an open problem whose resolution would solve the finite field isomorphism problem with run time nearly linear in the extension degree.
Exposé basé sur :
21 février 2019
Some contributions to the intersection problem with polydisks
Heure : 10h30, Salle : Marcel-Paul Schützenberger
An important class of systems in control theory is the class of
multidimensional systems in which information propagates in more than
one independent direction. At the core of the study of such systems is
the effective computation over the ring of rational fractions which
have no poles in the closed unit polydisk  . In
this context, two important questions related to the stability and the
stabilisation of these systems are
. In
this context, two important questions related to the stability and the
stabilisation of these systems are
-
Given a polynomial ideal
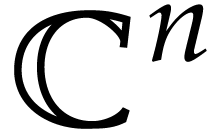 . Decide whether
or not
. Decide whether
or not 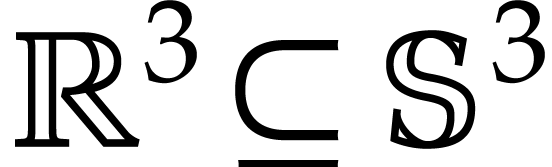 has zeros that lie in the unit
polydisk
has zeros that lie in the unit
polydisk 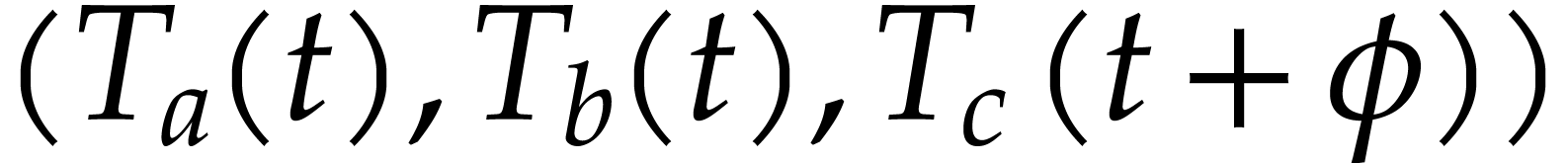 .
.
-
If not, compute a polynomial
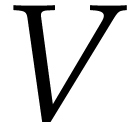 in the ideal
in the ideal
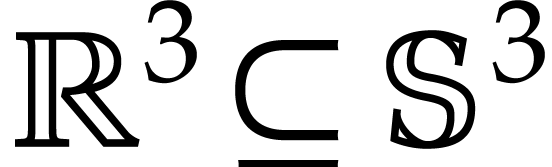 such that
such that 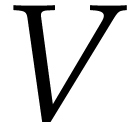 has no
zeros in the the unit polydisk
has no
zeros in the the unit polydisk 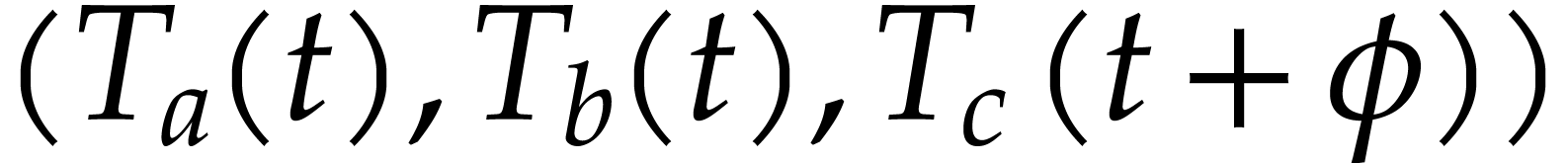 .
.
In [1], M. Strintzis states a fundamtental theorem showing that the
first question can be simplified in the case of principal ideals.
Namely, the theorem shows that the existence of complex zeros of a
polynomial 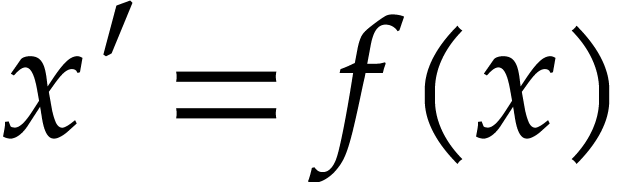 in
in 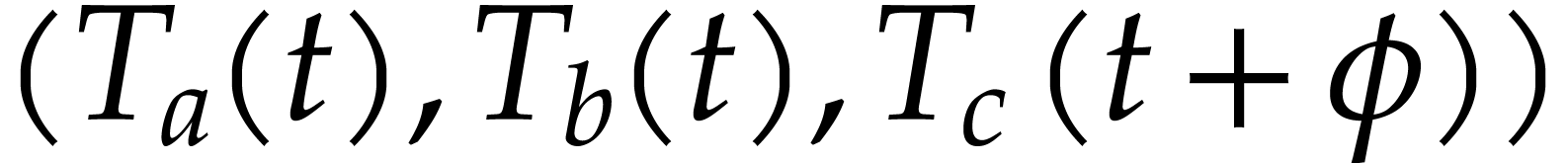 is
equivalent to the existence of complex zeros of
is
equivalent to the existence of complex zeros of 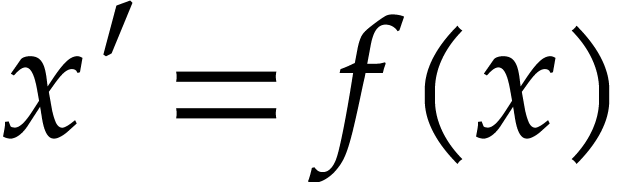 at one face of the polydisk, i.e.,
at one face of the polydisk, i.e., 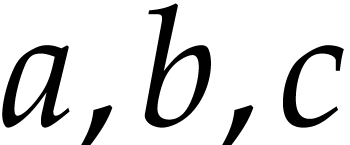 , or at the
poly-circle i.e.,
, or at the
poly-circle i.e., 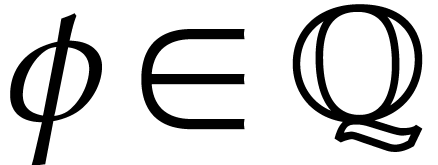 . The second question known
in the literature as the polydisk nullstelensatz is still
open for general systems.
. The second question known
in the literature as the polydisk nullstelensatz is still
open for general systems.
In this presentation, we extend the fundamental result of Strintzis to
some specific algebraic varieties, namely varieties of dimension one
in 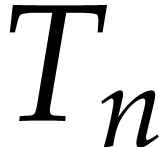 (algebraic curves). We also propose an
effective polydisk nullstellensatz in the case of
zero-dimensional ideals. As a consequence, important questions about
the stabilization of multidimensional systems can be answered using
simple algorithms based on computer algebra techniques.
(algebraic curves). We also propose an
effective polydisk nullstellensatz in the case of
zero-dimensional ideals. As a consequence, important questions about
the stabilization of multidimensional systems can be answered using
simple algorithms based on computer algebra techniques.
[1] Strintzis, M. Tests of stability of multidimensional filters. IEEE Transactions on Circuits and Systems, 24(8):432–437, 1977.
19 février 2019
Opérateurs de réduction : complétion, syzygies
et dualité de Koszul
Heure : 10h30, Salle : Marcel-Paul Schützenberger
La réécriture est une théorie combinatoire des relations d'équivalences où les propriétés de celles-ci sont déduites de leurs orientations. Une de ces propriétés est la confluence qui garantie la cohérence des calculs. Dans cet exposé, je présente une description des systèmes de réécriture à travers leurs représentations par des opérateurs de réduction. Cela permet d'obtenir des formulations de la confluence et de la procédure de complétion en termes de treillis. Je présente également des applications de cette approche au calcul des syzygies des systèmes de réécriture linéaires et à la dualité de Koszul. De celle-ci est issue la construction du complexe de Koszul, qui, lorsqu'il est acyclique, est une résolution minimale d'algèbres. Un critère introduit par Roland Berger garantie que le complexe de Koszul est une telle résolution minimale. En exploitant la structure de treillis des opérateurs de réduction, je propose via une homotopie contractante une preuve constructive de ce critère.
18 février 2019
Calcul de bases de Gröbner avec signatures à
coefficients dans un anneau principal
(Travail en commun avec
Heure : 10h30, Salle : Grace Hopper
Les algorithmes à signatures sont devenus une approche classique pour le calcul de bases de Gröbner pour des polynômes à coefficients dans un corps, et l'extension de cette technique à des polynômes à coefficients dans des anneaux a fait l'objet de travaux récents.
Dans ce travail, nous nous intéressons à deux algorithmes dûs à Möller (1988). Le premier de ces algorithmes permet de calculer des bases de Gröbner dites faibles, pourvu que l'anneau de coefficients soit noethérien et effectif. Nous montrons que, dans le cas où l'anneau des coefficients est principal, cet algorithme peut être adapté pour calculer des bases de Gröbner avec signatures. En particulier, l'algorithme garantit l'absence de chutes de signatures, ce qui permet d'adapter les critères de signatures classiques comme le critère singulier ou le critère F5.
Le second de ces algorithmes de Möller est quant à lui spécifique au cas des anneaux principaux, et permet de calculer une base de Gröbner forte de manière plus efficace que l'algorithme général. Nous montrons que cet algorithme peut également être adapté pour prendre en compte les signatures, et éviter un grand nombre de calculs redondants ou inutiles.
L'algorithme dédié aux anneaux principaux, contrairement à l'algorithme général, est également compatible avec les critères de Buchberger, notamment le critère de chaîne, et nous montrons que ce critère peut être ajouté de manière compatible avec les signatures.
Nous présentons enfin des résultats expérimentaux en termes de nombres de S-polynômes calculés, réduits ou écartés par les différents critères, mesurés sur une implantation « jouet » des algorithmes en Magma.
10 décembre 2018
Calcul de diagrammes de nœuds de Chebyshev
(Travail en commun avec D. Pecker, F. Rouillier, et C. Tran)
Heure : 10h30, Salle : Grace Hopper
Avec D. 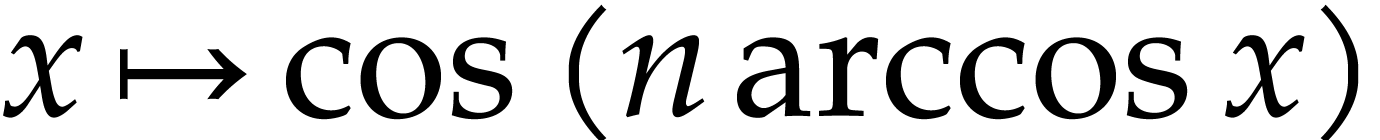 est un
nœud de Chebyshev, i.e. admet une
représentation polynomiale de la forme
est un
nœud de Chebyshev, i.e. admet une
représentation polynomiale de la forme 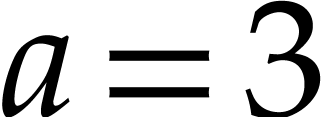 où
où 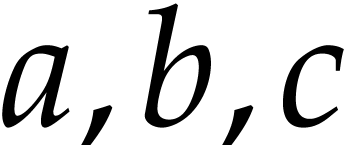 sont des entiers,
sont des entiers, 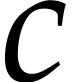 et
et 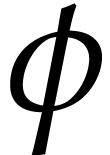 est le polynôme de Chebyshev
est le polynôme de Chebyshev 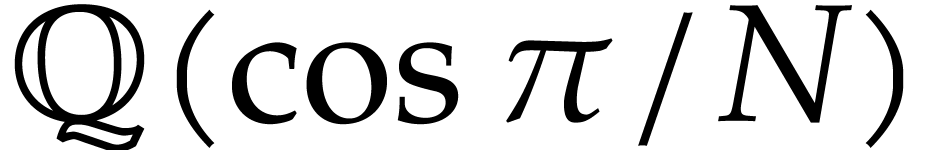 . Avec F.
. Avec F. 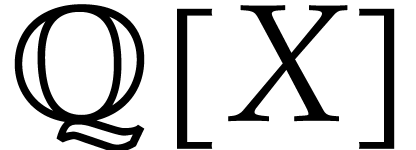 ,
, 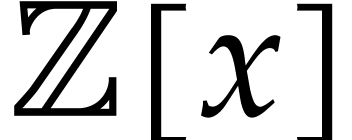 ,
, 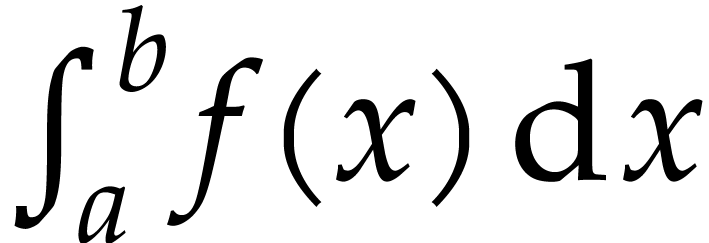 fixé et
fixé et  variant). L'exposé abordera les différents aspects de ce
problème et sa généralisation. Il apparaît
judicieux, de travailler dans des extensions cyclotomiques
réelles
variant). L'exposé abordera les différents aspects de ce
problème et sa généralisation. Il apparaît
judicieux, de travailler dans des extensions cyclotomiques
réelles  et d'utiliser la base des
polynômes unitaires de Chebyshev
et d'utiliser la base des
polynômes unitaires de Chebyshev 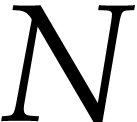 .
.
Référence : https://hal.archives-ouvertes.fr/hal-01232181
12 février 2018
Intrinsic and Apparent Singularities in Flat Differential Systems
(Travail en commun avec Jean Lévine et François Ollivier)
Heure : 14h, Salle : Grace Hopper
We study the singularities of locally flat systems, motivated by the solution, if it exists, of the global motion planning problem for such systems. More precisely, flat outputs may be only locally defined because of the existence of points where they are singular (a notion that will be made clear later), thus preventing from planning trajectories crossing these points. Such points are of different types. Some of them can be easily ruled out by considering another non singular flat output, defined on an open set intersecting the domain of the former one and well defined at the point in question. However, it might happen that no well-defined flat outputs exist at all at some points. We call these points intrinsic singularities and the other ones apparent. A rigorous definition of these points is introduced in terms of atlas and charts in the framework of the differential geometry of jets of infinite order and Lie-Bäcklund isomorphisms. We then give a criterion allowing to effectively compute intrinsic singularities. Finally, we show how our results apply to global motion planning of the well-known example of non-holonomic car. Flat differential systems, singularities, global motion planning.
8 janvier 2018
Integer polynomial sparse interpolation with near-optimal complexity
Heure : 14h, Salle : Henri Poincaré
We investigate algorithms to discover the nonzero coefficients and
exponents of an unknown sparse polynomial, provided a way to evaluate
the polynomial over any modular ring. This problem has been of
interest to the computer algebra community for decades, and its uses
include multivariate polynomial GCD computation, factoring, and sparse
polynomial arithmetic. Starting with the early works of Zippel, Ben-Or
and Tiwari, and Kaltofen, one line of investigation has a key
advantage in achieving the minimal number of evaluations of the
polynomial, and has received considerable attention and improvements
over the years. It is closely related to problems in coding theory and
exponential analysis. The downside, however, is that these methods are
not polynomial-time over arbitrary fields. A separate line of work
starting with Garg and Schost has developed a different approach that
works over any finite field. After years of improvements, the
complexity of both approaches over 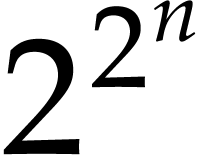 is
currently the same. They scale well in most aspects except for the
degree; the bit complexity in both cases is currently cubic in the
bit-lengths of the exponents. By careful combination of the techniques
in both approaches and a few new tricks, we are now able to overcome
this hurdle. We present an algorithm whose running time is
softly-linear in the size of the output and performs nearly the
minimal number of evaluations of the unknown polynomial. Preliminary
implementation results indicate good promise for practical use when
the unknown polynomial has a moderate number of variables and/or large
exponents.
is
currently the same. They scale well in most aspects except for the
degree; the bit complexity in both cases is currently cubic in the
bit-lengths of the exponents. By careful combination of the techniques
in both approaches and a few new tricks, we are now able to overcome
this hurdle. We present an algorithm whose running time is
softly-linear in the size of the output and performs nearly the
minimal number of evaluations of the unknown polynomial. Preliminary
implementation results indicate good promise for practical use when
the unknown polynomial has a moderate number of variables and/or large
exponents.
11 décembre 2017
Numerical integration in complex interval arithmetic
Heure : 10h30, Salle : Grace Hopper
We present a new implementation of validated arbitrary-precision
numerical evaluation of definite integrals 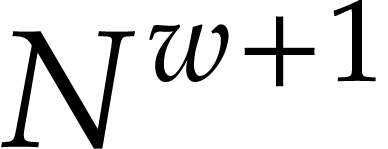 ,
available in the Arb library. The code uses a version of the Petras
algorithm, which combines adaptive subdivision with Gauss-Legendre
(GL) quadrature, evaluating the integrand on complex intervals
surrounding the path of integration to obtain rigorous error bounds.
The first part of the talk discusses the general algorithm and its
performance for interesting families of integrals. The second part,
which is based on joint work with Marc Mezzarobba, discusses the fast
computation of GL quadrature nodes with rigorous error bounds. It is
well known that GL quadrature achieves a nearly optimal rate of
convergence for analytic integrands with singularities well isolated
from the path of integration, but due to the cost of generating GL
quadrature nodes, the more slowly converging Clenshaw-Curtis and
double exponential quadrature rules have often been favored when an
accuracy of several hundreds or thousands of digits is required. We
consider the asymptotic and practical aspects of this problem. An
order-of-magnitude speedup is obtained over previous code for
computing GL nodes with simultaneous high degree and precision, which
makes GL quadrature viable even at very high precision.
,
available in the Arb library. The code uses a version of the Petras
algorithm, which combines adaptive subdivision with Gauss-Legendre
(GL) quadrature, evaluating the integrand on complex intervals
surrounding the path of integration to obtain rigorous error bounds.
The first part of the talk discusses the general algorithm and its
performance for interesting families of integrals. The second part,
which is based on joint work with Marc Mezzarobba, discusses the fast
computation of GL quadrature nodes with rigorous error bounds. It is
well known that GL quadrature achieves a nearly optimal rate of
convergence for analytic integrands with singularities well isolated
from the path of integration, but due to the cost of generating GL
quadrature nodes, the more slowly converging Clenshaw-Curtis and
double exponential quadrature rules have often been favored when an
accuracy of several hundreds or thousands of digits is required. We
consider the asymptotic and practical aspects of this problem. An
order-of-magnitude speedup is obtained over previous code for
computing GL nodes with simultaneous high degree and precision, which
makes GL quadrature viable even at very high precision.
— Pause déjeuner de 11h45 à 13h45 —
Numerical approximation of multiple isolated roots of analytic
systems
(Travail en commun avec Marc Giusti)
Heure : 14h, Salle : Henri Poincaré
It is classical that the convergence of the Newton's method at the neighborhood of a singular isolated root of a system of equations is no longer quadratic. It may even diverge. To fix this problem we purpose a new operator, named +singular Newton operator, generalizing the classical Newton operator defined regular case. To do so we construct a finite sequence of equivalent systems named deflation sequence where the multiplicity of the root drops strictly between two successive elements of the sequence. Hence the root is a regular root for the last system. Then there exits a regular square system extracted of this one named deflated system. The Singular Newton operator is defined as the classical Newton operator associated to this deflated system.
The main idea of the construction of the deflation sequence is the following. Since the Jacobian matrix is rank deficient at the root, it means that there exists relation between the lines (respectively columns) of this Jacobian matrix. These relations are given by the Schur complement of the Jacobian matrix. The result is that when the elements of the Schur complement are added to the initial system, we call this operation kernelling, one obtains an equivalent system where the multiplicity of the root has dropped. In this way, a sequence of equivalent system can be defined iteratively.
Finally we perform a local 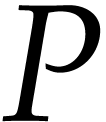 -theory of Smale of
this Singular Newton operator.
-theory of Smale of
this Singular Newton operator.
6 novembre 2017
Indécidabilité de l'appartenance à un
idéal aux dérivées partielles de type fini
(d'après Umirbaiev)
Heure : 10h30, Salle : Grace Hopper
On sait que l'appartenance à un idéal
différentiel est indécidable [1]. On montre aussi que
l'appartenance à un idéal différentiel premier ou
radiciel est décidable, ce qui est une conséquence
directe de la théorie des ensembles caractéristiques
développée par Ritt [2]. On a également des
résultats de décidabilité pour des idéaux
différentiels isobares [1]. Le problème restait ouvert
pour des idéaux différentiels de type fini. Dans un
article récent, Umirbaiev [3] a montré que
l'appartenance à un idéal aux dérivées
partielles (donc avec au moins 2 dérivations) est
indécidable. La démonstration repose sur une
construction permettant d'associer à une machine de Minsky
à 2 bandes un idéal stable pour 2 dérivations.
Une machine de Minsky est une variante des machines de Turing. Les
deux bandes sont finies à un bout et infini à l'autre.
Il n'y a rien d'écrit dans chaque case, pas même la
position, mais on peut repérer que la machine est sur la
première case d'une bande. On peut associer à tout sous
ensemble récursivement énumérable 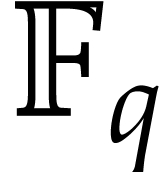 de
de  une machine de Minsky sans
cycle qui, partant de la case
une machine de Minsky sans
cycle qui, partant de la case 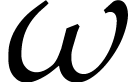 s'arrête
si et seulement si le nombre
s'arrête
si et seulement si le nombre 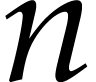 est dans
est dans 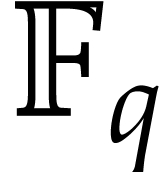 . L'appartenance à l'idéal
différentiel correspondant ne peut être
décidée en général, puisqu'il existe des
ensembles de nombres entiers récursivement
énumérables mais non récursifs. Ce travail laisse
ouvert la situation d'un idéal différentiel ordinaire de
type fini, sur laquelle nous tenterons de jeter quelques
lumières.
. L'appartenance à l'idéal
différentiel correspondant ne peut être
décidée en général, puisqu'il existe des
ensembles de nombres entiers récursivement
énumérables mais non récursifs. Ce travail laisse
ouvert la situation d'un idéal différentiel ordinaire de
type fini, sur laquelle nous tenterons de jeter quelques
lumières.
[1] G. Gallo, B. Mishra, F. Ollivier (1991), « Some constructions in rings of differential polynomials », In: Mattson H.F., Mora T., Rao T.R.N. (eds) Applied Algebra, Algebraic Algorithms and Error-Correcting Codes. AAECC 1991. Lecture Notes in Computer Science, vol 539. Springer, Berlin, Heidelberg.
[2] J. F. Ritt, Differential algebra, AMS, 1950.
[3] U. Umirbaiev, « Algorithmic problems for differential polynomial algebras », Journal of Algebra, Volume 455, 1 June 2016, Pages 77-92.
— Pause déjeuner de 11h45 à 13h45 —
Calcul symbolique des intégrales premières de champs
de vecteur polynomiaux du plan
Heure : 14h, Salle : Grace Hopper
Soit 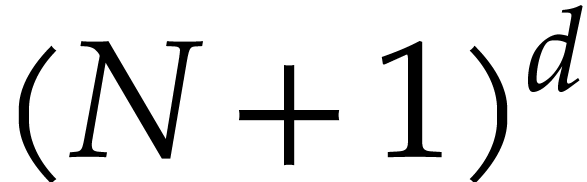 un champ de vecteur polynomial du plan.
Nous présenterons un algorithme calculant les invariant
différentiels rationnels de
un champ de vecteur polynomial du plan.
Nous présenterons un algorithme calculant les invariant
différentiels rationnels de 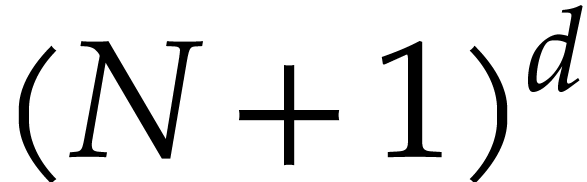 jusqu'à une certaine borne
jusqu'à une certaine borne  donnée par l'utilisateur. Ces invariant différentiels
pour un feuilletage associé à un champ de vecteur du
plan ont été classifiés par G.
Casale et il s'avère qu'il correspondent aux intégrales
premières de
donnée par l'utilisateur. Ces invariant différentiels
pour un feuilletage associé à un champ de vecteur du
plan ont été classifiés par G.
Casale et il s'avère qu'il correspondent aux intégrales
premières de 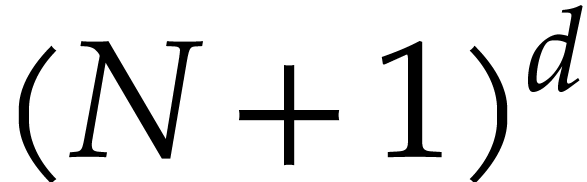 d'un certain type,
précisément rationnels, darbouxien, liouvillien et
ricatti. Dans chaque cas, nous introduirons une notion de courbe
extatique, généralisant celle pour les intégrales
premières rationnelles. Une nouveauté est que ces
courbes extatiques peuvent détecter (dans des cas non
génériques) des intégrales premières de
degré plus grand que
d'un certain type,
précisément rationnels, darbouxien, liouvillien et
ricatti. Dans chaque cas, nous introduirons une notion de courbe
extatique, généralisant celle pour les intégrales
premières rationnelles. Une nouveauté est que ces
courbes extatiques peuvent détecter (dans des cas non
génériques) des intégrales premières de
degré plus grand que  . La sortie de
l'algorithme est une équation différentielle dont les
solutions correspondent aux intégrales premières
recherchées. Ces solutions peuvent parfois être
simplifiées, pouvant mener à des intégrales
premières de degré très élevé dus
à des phénomènes arithmétiques. Le cout
probabiliste de l'algorithme est en
. La sortie de
l'algorithme est une équation différentielle dont les
solutions correspondent aux intégrales premières
recherchées. Ces solutions peuvent parfois être
simplifiées, pouvant mener à des intégrales
premières de degré très élevé dus
à des phénomènes arithmétiques. Le cout
probabiliste de l'algorithme est en 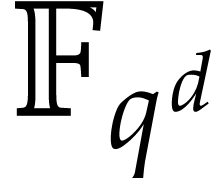 , et peut
être transformé en algorithme déterministe avec un
cout supplémentaire.
, et peut
être transformé en algorithme déterministe avec un
cout supplémentaire.
9 octobre 2017
Task-based parallelism and heterogeneous deployment for the N-body
problem
Heure : 14h, Salle : Grace Hopper
The  -body problem, describing the computation
of all pairwise interactions among
-body problem, describing the computation
of all pairwise interactions among  bodies, is
one of the key kernels for high performance computing (e.g. in
astrophysics, molecular dynamics, electromagnetics, fluid
mechanics…). Efficient algorithms (Fast Multipole Method, Dual
Tree Traversal) have been introduced to solve this
bodies, is
one of the key kernels for high performance computing (e.g. in
astrophysics, molecular dynamics, electromagnetics, fluid
mechanics…). Efficient algorithms (Fast Multipole Method, Dual
Tree Traversal) have been introduced to solve this  -body
problem with linear runtime complexity. Their deployment on both
multi-core and many-core architectures is crucial, but can raise
multiple challenges, regarding performance, portability and
programmability. We will here present how these difficulties can be
overcome on several (homogeneous and heterogeneous) parallel
architectures for astrophysical simulations.
-body
problem with linear runtime complexity. Their deployment on both
multi-core and many-core architectures is crucial, but can raise
multiple challenges, regarding performance, portability and
programmability. We will here present how these difficulties can be
overcome on several (homogeneous and heterogeneous) parallel
architectures for astrophysical simulations.
8 juin 2017
Automatic Asymptotics in Isabelle/HOL
Heure : 14h, Salle : Henri Poincaré
This talk will give a brief overview of
6 mars 2017
Morphisme de Frobenius et FFT
Heure : 10h30, Salle : Claude Shannon
On considère un polynôme  à
coefficients dans le corps fini
à
coefficients dans le corps fini 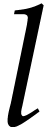 dont on
souhaite calculer la transformée de Fourier discrète
dont on
souhaite calculer la transformée de Fourier discrète
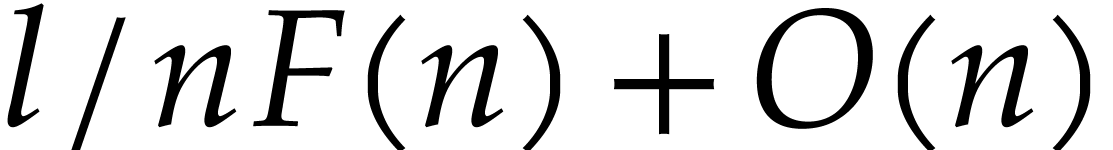 où
où 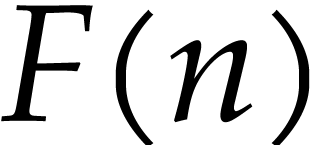 est une
racine primitive
est une
racine primitive 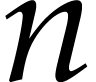 -ième de
l'unité. En général, une telle racine existe
seulement dans une certaine extension de corps
-ième de
l'unité. En général, une telle racine existe
seulement dans une certaine extension de corps 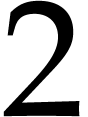 .
Nous verrons comment il est possible, en exploitant les
propriétés du morphisme de Frobenius, de gagner un
facteur
.
Nous verrons comment il est possible, en exploitant les
propriétés du morphisme de Frobenius, de gagner un
facteur 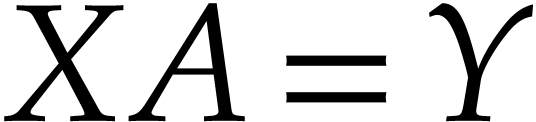 par rapport au calcul de la
transformée de Fourier d'un polynôme
par rapport au calcul de la
transformée de Fourier d'un polynôme 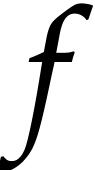 à coefficients dans
à coefficients dans 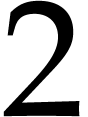 . Ce travail est
l'analogue pour les corps finis du résultat bien connu selon
lequel la transformée de Fourier est 2 fois plus rapide
à calculer pour un polynôme à coefficients
réels que pour un polynôme à coefficients
complexes.
. Ce travail est
l'analogue pour les corps finis du résultat bien connu selon
lequel la transformée de Fourier est 2 fois plus rapide
à calculer pour un polynôme à coefficients
réels que pour un polynôme à coefficients
complexes.
— Pause déjeuner de 11h45 à 13h45 —
Fast systematic encoding of multiplicity codes
Heure : 14h00, Salle : Grace Hopper
Multiplicity codes are a relatively new family of polynomial codes introduced by Kopparty, Saraf and Yekhanin (STOC'11). They generalise the classical family of Reed-Muller codes by augmenting their construction to include the evaluations of Hasse derivatives up to a given order. In this talk, we present a quasi-linear time systematic encoding algorithm for multiplicity codes. For the special case of Reed-Muller codes, the encoding algorithm simply applies existing multivariate interpolation and evaluation algorithms of van der Hoeven and Schost (2013). The general encoding algorithm is obtained by generalising their algorithms to address Hermite type interpolation and evaluation problems.
12 décembre 2016
SPECTRA: a Maple library for linear matrix inequalities
Heure : 14h15, Salle : Grace Hopper
Linear matrix inequalities (LMI) are a class of convex feasibility problems appearing in different applicative contexts. For instance, checking the asymptotic stability à la Lyapunov for linear differential systems, or computing nonnegativity certificates for multivariate polynomials, are LMI. I will discuss an approach based on techniques from real algebraic geometry to compute exact solutions to LMI, and what informations are carried by this representation. The related algorithms are implemented in a Maple library called SPECTRA, and part of the talk will be dedicated to discuss results on experiments on interesting examples.
Généralisation de la transformée de Fourier
tronquée pour des ordres quelconques
Heure : 15h45, Salle : Grace Hopper
La transformée de Fourier tronquée (TFT) vise à
calculer seulement certaines valeurs d'une FFT classique. En
évitant de calculer les valeurs intermédiaires qui
n'interviennent pas dans le calcul des points d'évaluation
souhaités, on réduit de manière notable la
durée de l'opération : pour calculer 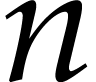 points d'évaluation sur
points d'évaluation sur  , le coût
est réduit à
, le coût
est réduit à  opérations
élémentaires, où
opérations
élémentaires, où  est le
coût d'une FFT classique. Cela permet de réduire les
effets de saut de complexité dans les algorithmes
d'évaluation-interpolation (typiquement pour la multiplication
de polynômes). Dans la formulation initiale de la TFT, on
suppose que
est le
coût d'une FFT classique. Cela permet de réduire les
effets de saut de complexité dans les algorithmes
d'évaluation-interpolation (typiquement pour la multiplication
de polynômes). Dans la formulation initiale de la TFT, on
suppose que  est une puissance de
est une puissance de  , mais certaines applications, par exemple pour des corps
finis, peuvent nécessiter une forme plus générale
pour
, mais certaines applications, par exemple pour des corps
finis, peuvent nécessiter une forme plus générale
pour  . Après avoir rappelé
rapidement le principe de la FFT, et celui de la TFT quand
. Après avoir rappelé
rapidement le principe de la FFT, et celui de la TFT quand 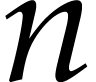 est une puissance de
est une puissance de 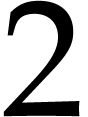 , nous
verrons comment ces techniques peuvent être adaptées pour
, nous
verrons comment ces techniques peuvent être adaptées pour
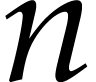 quelconque.
quelconque.
23 mai 2016 — Journée « théorie de contrôle »
Commande sans modèle : a-t-on toujours besoin d'un
modèle pour appliquer les mathématiques à
l'industrie ?
Heure : 10h30, Salle : Marcel-Paul Schützenberger
On expose les principes généraux de la « commande sans modèle », qui permet de réguler avec précision et facilité bien des dispositifs concrets sans recourir à une modélisation mathématique, toujours difficile, voire impossible, à obtenir. On passe en revue de nombreux exemples. En conclusion, quelques considérations générales sur les mathématiques appliquées, notamment en automatique, tentent de placer cet exposé dans un cadre plus général.
— Pause déjeuner de 12h à 13h30 —
L'apport du calcul formel dans une démarche système
Heure : 14h, Salle : Marcel-Paul Schützenberger
Exemples d'applications du calcul formel pour le CNES, l'analyse de sensibilité des modèles Simulink, et d'autres applications.
Commande sans modèle : de la théorie à la
pratique
Heure : 15h30, Salle : Marcel-Paul Schützenberger
On détaille la mise en oeuvre de la commande sans modèle. Des méthodes nouvelles d'estimation, d'essence algébrique et faciles à implanter, en sont le fil conducteur. On étudiera les contraintes pratiques qu'elles doivent satisfaire. La conclusion portera sur la complexité actuelle de l'algorithme.
9 mai 2016
Estimates on the number of solutions of equations over a finite field and applications
Heure : 10h30, Salle : Paul Schützenberger
The set of rational solutions of polynomial systems over a finite field is a classical subject of study, whose origins can be traced back to works of Gauss and Jacobi, and has contributions of Hardy, Littlewood, Chevalley, Davenport, Weil, Lang and Deligne, among others. In this talk we shall discuss recent results of existence of solutions and estimates on the number of solutions of polynomial systems over a finite field. We shall also comment on applications of these estimates to problems in coding theory and combinatorics.
21 septembre 2015 — Journée Mathemagix
Borderbasix
Heure : 10h30, Salle : Grace Hopper
Border bases form an alternative method to Groebner bases for
polynomial system solving. The advantage is an increased flexibility
for the choice of critical pairs, which is particularly useful for
increasing the numerical stability of numerical solvers. In this talk,
I will present the
Advances in the C++ libraries Numerix, Algebramix, Multimix and Factorix
Heure : 11h, Salle : Grace Hopper
I will present recent implementations added to the C++ Mathemagix libraries Numerix, Algebramix, Multimix and Factorix. In particular these libraries now benefit from an efficient support of AVX2 instruction set for numeric and modular arithmetic. I will report on applications and performances. Parts of these works are joint with Joris van der Hoeven and Guillaume Quintin.
— Pause déjeuner de 11h30 à 14h —
Geometric computation with Mathemagix
Heure : 14h, Salle : Grace Hopper
I will describe the packages
Lindalg: Mathemagix package for symbolic resolution of linear differential systems with singularities
Heure : 14h30, Salle : Grace Hopper
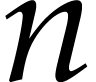 -th order linear differential equations and
first order linear differential systems. At ordinary points, it
suffices to consider Taylor series (power series). Any engineering
student or scientist is familiar with their resolution procedure and
popular computer systems always consider a package for this goal.
However, singular points require further investigation based on an
analysis of a Newton polygon and matricial manipulations. Differential
equations with singularities arise from countless applications and
encompass a vast body of contemporary academic literature. The package
-th order linear differential equations and
first order linear differential systems. At ordinary points, it
suffices to consider Taylor series (power series). Any engineering
student or scientist is familiar with their resolution procedure and
popular computer systems always consider a package for this goal.
However, singular points require further investigation based on an
analysis of a Newton polygon and matricial manipulations. Differential
equations with singularities arise from countless applications and
encompass a vast body of contemporary academic literature. The package
On the other hand, the new package
— Pause café de 15h à 15h30 —
Programming symbolic expressions using the
Heure : 15h30, Salle : Grace Hopper
We will show how to program symbolic expressions using the
Lacunaryx : calcul des facteurs de degré borné de polynômes lacunaires
Heure : 16h, Salle : Grace Hopper
Mon exposé présentera une nouvelle bibliothèque
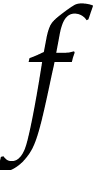 en
représentation creuse et une borne
en
représentation creuse et une borne 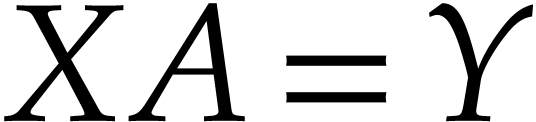 de
degré et retournent la liste des facteurs de degré au
plus
de
degré et retournent la liste des facteurs de degré au
plus 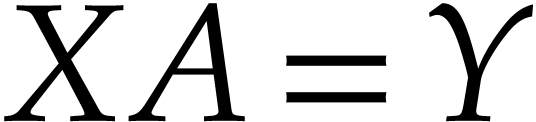 de
de 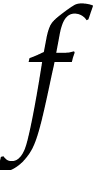 . La
complexité de ces algorithmes est polynomiale en la taille de
la représentation creuse, c'est-à-dire en particulier
poly-logarithmique en le degré.
. La
complexité de ces algorithmes est polynomiale en la taille de
la représentation creuse, c'est-à-dire en particulier
poly-logarithmique en le degré.
24 novembre 2014
Un algorithme de décision pour l'intégrabilité de systèmes de Pfaff
Heure : 11h, Salle : Philippe Flajolet
On montre un critère qui permet de décider si un système différentiel-algébrique de Pfaff a une solution. La méthode induit un algorithme de décision dont sa complexité est doublement exponentielle dans le nombre d'inconnues et de variables indépendantes, et polynomial dans le degré et le nombre des polynômes qui apparaissent dans le système.
Un résumé subjectif sur le 17-ième problème de Smale : les quatre pattes de SUMO
Heure : 15h, Salle : Marcel-Paul Schützenberger
L'exposé contiendra une vision personnelle sur les quatre pattes de la résolution du Problème 17-ième de Smale :
“Can a zero of 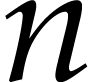 complex polynomial
equations in
complex polynomial
equations in 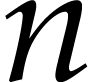 unknowns be found
approximately, on the average, in polynomial time with a uniform
algorithm?”
unknowns be found
approximately, on the average, in polynomial time with a uniform
algorithm?”
Ses quatre pattes, à mon avis, sont : le conditionnement, l'opérateur, l'homotopie et la géométrie intégrale (voire probabilité). La dernière étant la plus efficace à donner des bonnes réponses jusqu'à présent.
17 novembre 2014
On the Complexity of Solving Bivariate Systems
Heure : 11h, Salle : Philippe Flajolet
We present an algorithm for the symbolic solution of bivariate
polynomial systems with coefficients in  with
essentially optimal bit complexity. The core of the algorithm is a
classical Newton iteration procedure. New ingredients are needed,
though, such as Kedlaya-Umans' modular composition algorithm and
deflation techniques due to Lecerf.
with
essentially optimal bit complexity. The core of the algorithm is a
classical Newton iteration procedure. New ingredients are needed,
though, such as Kedlaya-Umans' modular composition algorithm and
deflation techniques due to Lecerf.
Cette page web fait partie du projet
 Version Pdf
Version Pdf