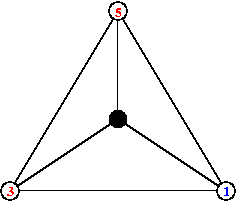
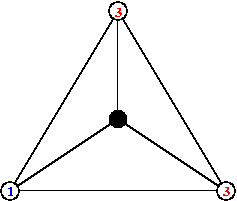
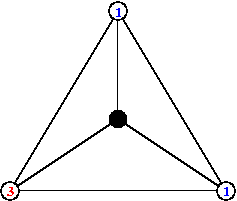
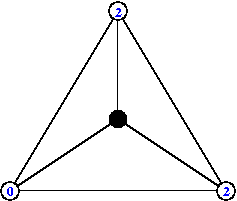
On peut facilement généraliser à tout graphe la notion précédente. En effet soit G un graphe à n+1 sommets numérotés de 0 à n. On dira que le sommet 0 est le puits c'est à dire qu'il jouera le rôle des bords de la grille dans l'exemple précédent. Sur chaque sommet on met un certain nombre de grains de sable et on dirat qu'un sommet est instable s'il contient un nombre de grains supérieur ou égal à son degré. Dans ce cas ce sommet perd d grains de sable où d est son degré et il donne à chacun de ses voisins un grain. Si un grain arrive sur le sommet 0 alors il est perdu.




A la fin de ce processus, on retombe sur une configuration stable, c'est à dire une configuration ou aucun état ne peut s'ébouler.
Dans tous les exemples précédents, on remarque que si
plusieurs éboulements sont possibles dans une configuration
alors on les exécute en parallele. Mais on peut se demander ce
qui se passerait si ces opérations sont exécutées
séquentillement.
On démontre dans ce cas que la configuration stable finale
obtenue est indépendant de l'ordre choisi pour ébouler
les sommets instables. Une méthode simple pour démontrer
ce résultat consiste à remarquer que si deux sommets
sont instables alors on obtient la même configuration en
éboulant le premier sommet puis le deuxième ou l'inverse.