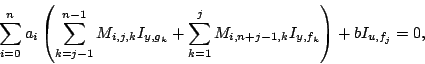suivant: Identification avec retard
monter: Une méthode d'identification pour
précédent: Introduction
Pour alléger les formules, nous écrirons le système sous la forme:
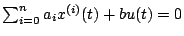 , avec
, avec 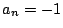 . La
sortie est
. La
sortie est  , où
, où 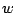 désigne le bruit, que nous
supposons tel que
désigne le bruit, que nous
supposons tel que
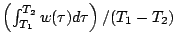 tend vers
tend vers 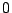 quand
quand 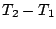 tend vers l'infini. L'idée de base est
d'utiliser une famille de fonctions
tend vers l'infini. L'idée de base est
d'utiliser une famille de fonctions 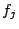 ,
, 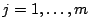 telles que
telles que
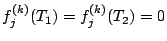 pour
pour 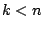 .
.
On pose
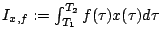 . En intégrant par parties, on aura
. En intégrant par parties, on aura
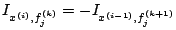 , si
, si 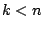 , et donc
, et donc
 . On peut donc calculer la valeur
des coefficients
. On peut donc calculer la valeur
des coefficients 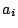 et
et 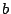 en résolvant le système
en résolvant le système
pour 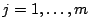 , si
, si 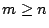 . Pour
. Pour 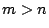 , ce système sera
résolu par la méthode des moindres carrés.
, ce système sera
résolu par la méthode des moindres carrés.
Si l'on se donne une famille 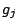 ,
, 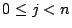 telle que
telle que
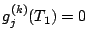 pour
pour 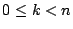 et
et
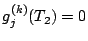 pour
pour 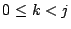 , avec
, avec
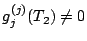 , on obtient alors
, on obtient alors
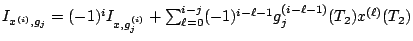 .
On estime
.
On estime
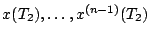 en
résolvant le système
en
résolvant le système
pour
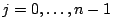 . Ces équations se déduisent
immédiatement de
. Ces équations se déduisent
immédiatement de
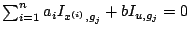 .
.
Par exemple, on peut prendre
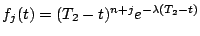 , et
, et
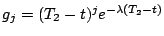 . Ces fonctions satisfont
les hypothèses pour
. Ces fonctions satisfont
les hypothèses pour 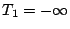 . Si l'on pose
. Si l'on pose
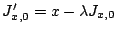
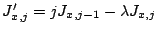 si
si 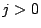 , avec
les conditions initiales
, avec
les conditions initiales 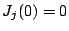 ,
, 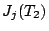 tend vers
tend vers
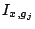 pour
pour
 et vers
et vers
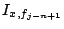 pour
pour
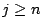 , quand
, quand 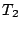 tend vers l'infini. La convergence est rapide
pour
tend vers l'infini. La convergence est rapide
pour 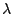 suffisament grand. On a
suffisament grand. On a
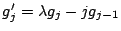 et une relation similaire pour les
et une relation similaire pour les 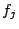 . On a donc
. On a donc
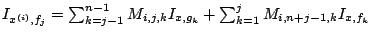 , où
les matrices
, où
les matrices 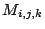 satisfont des relations de récurrence
simples, ce qui facilite les calculs.
On obtient en un temps
satisfont des relations de récurrence
simples, ce qui facilite les calculs.
On obtient en un temps  générique et suffisament grand une
bonne approximation des paramètres
générique et suffisament grand une
bonne approximation des paramètres 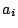 et
et 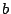 en résolvant
le système
en résolvant
le système
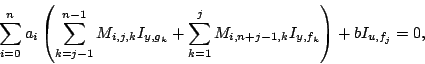
que nous noterons 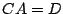 , où
, où
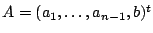 . Comme il se peut que pour certaines valeurs le rang du
système ne s'annule, il est préférable de ne pas le
résoudre directement mais d'en chercher la solution par une
méthode de gradient, en se donnant de nouvelles variables
. Comme il se peut que pour certaines valeurs le rang du
système ne s'annule, il est préférable de ne pas le
résoudre directement mais d'en chercher la solution par une
méthode de gradient, en se donnant de nouvelles variables
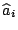 et
et
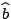 , et en intégrant le système
, et en intégrant le système
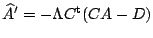 . Ce choix permet de conserver des valeurs précises lorsque
. Ce choix permet de conserver des valeurs précises lorsque
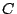 devient mal conditionnée et de réduire encore l'influence
du bruit. Les valeurs de
devient mal conditionnée et de réduire encore l'influence
du bruit. Les valeurs de 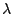 et de
et de 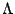 résultent d'un
compromis entre la vitesse de convergence souhaitée et la
précision recherchée.
résultent d'un
compromis entre la vitesse de convergence souhaitée et la
précision recherchée.
Exemple 1
On a pris
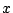
solution de l'équation
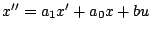
,
où
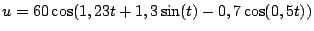
, avec les conditions
initiales
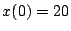
et
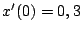
. On a choisi un bruit gaussien avec
un écart type de
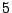
. La sortie est échantillonnée à
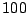
Hz. On a pris
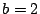
,
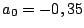
,
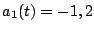
si
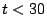
et
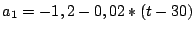
sinon. Les courbes de la
figure
1 résument les résultats obtenus
pour
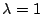
et
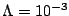
.
On voit qu'après une phase de convergence,
l'approximation obtenue est excellente. La précision de
l'évaluation des coefficients est naturellement moins bonne quand
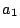 commence à varier. Toutefois, les évaluations de
commence à varier. Toutefois, les évaluations de 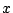 et
et 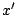 demeurent assez précises.
demeurent assez précises.



suivant: Identification avec retard
monter: Une méthode d'identification pour
précédent: Introduction
Francois Ollivier
2005-03-29
![]() , avec
, avec ![]() . La
sortie est
. La
sortie est ![]() , où
, où ![]() désigne le bruit, que nous
supposons tel que
désigne le bruit, que nous
supposons tel que
![]() tend vers
tend vers ![]() quand
quand ![]() tend vers l'infini. L'idée de base est
d'utiliser une famille de fonctions
tend vers l'infini. L'idée de base est
d'utiliser une famille de fonctions ![]() ,
, ![]() telles que
telles que
![]() pour
pour ![]() .
.
![]() . En intégrant par parties, on aura
. En intégrant par parties, on aura
![]() , si
, si ![]() , et donc
, et donc
![]() . On peut donc calculer la valeur
des coefficients
. On peut donc calculer la valeur
des coefficients ![]() et
et ![]() en résolvant le système
en résolvant le système
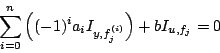
![]() ,
, ![]() telle que
telle que
![]() pour
pour ![]() et
et
![]() pour
pour ![]() , avec
, avec
![]() , on obtient alors
, on obtient alors
![]() .
On estime
.
On estime
![]() en
résolvant le système
en
résolvant le système
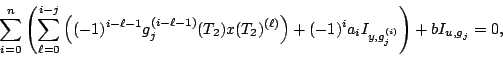
![]() , et
, et
![]() . Ces fonctions satisfont
les hypothèses pour
. Ces fonctions satisfont
les hypothèses pour ![]() . Si l'on pose
. Si l'on pose
![]()
![]() si
si ![]() , avec
les conditions initiales
, avec
les conditions initiales ![]() ,
, ![]() tend vers
tend vers
![]() pour
pour
![]() et vers
et vers
![]() pour
pour
![]() , quand
, quand ![]() tend vers l'infini. La convergence est rapide
pour
tend vers l'infini. La convergence est rapide
pour ![]() suffisament grand. On a
suffisament grand. On a
![]() et une relation similaire pour les
et une relation similaire pour les ![]() . On a donc
. On a donc
![]() , où
les matrices
, où
les matrices ![]() satisfont des relations de récurrence
simples, ce qui facilite les calculs.
On obtient en un temps
satisfont des relations de récurrence
simples, ce qui facilite les calculs.
On obtient en un temps ![]() générique et suffisament grand une
bonne approximation des paramètres
générique et suffisament grand une
bonne approximation des paramètres ![]() et
et ![]() en résolvant
le système
en résolvant
le système