Examples

The result has a long history. In [6], a faulty scheme of proof (for which the first author of this paper is fully responsible) was proposed. The main idea was to consider the extension $K_{2}/L$ and use the filtration defined by the order to construct the linearizing output. Let $K_{r}$ be the algebraic closure of $k(z, z', \ldots, z^{(r)})$ in $K_{2}$ and $L_{r}:=\overline{L}\cap K_{r}$. We expect to build incrementaly a linearizing output by taking $Y_{0}$ to be a transcendence basis of $L_{0}$, then $Y_{0}\cup Y_{0}'\cup Y_{1}$ to be a transcendence basis of $L_{1}$, etc. Provided that $Y=\cup_{i} Y_{i}$ is differentially independent, it is a linearizing output. But, this is not allways the case.

Example 5. -- Let $L:=k\langle z_{1}', z_{3} + z_{1}'z_{2}, z_{4} + (z_{1}')^{2}z_{2}, \ldots, z_{n} + (z_{1}')^{n-2}z_{2}\rangle$. Then, $L_{0}=k$ but $L_{1}$ is generated by $z_{1}'$, $z_{i} + (z_{1}')^{i-2}z_{2}$ for $i\in[3,n]$ and $z_{i}'+(z_{1}')^{i-2}z_{2}'-(i-2)(z_{1}')^{i-3}(z_{3}'+z_{1}'z_{2}')$ for $i\in[4,n]$. That family of elements is too large to be differentialy independent.

Of course, one sees that is is enough to modify the filtration and take, e.g. $K_{r}$ to be generated by derivatives of $z_{1}$ up to order $r+1$ and of the remaining variables up to order $r$. But it is not always possible to save the situation in such a simple way.

A different idea is to use the structure of a characteristic set ${\cal A}$ of the prime ideal associated to the extension $L\langle z\rangle/L$. Let $A_{i}$ be an element of ${\cal A}$, we substitute to the non leading derivatives of $A_{i}$ generic values in $k$, defining new equations $B_{i}$ in the leading derivatives $\upsilon_{A_{i}}$. This set of equation defines an algebraic extension of $L$ and the family $\upsilon_{A_{i}}$ is a good candidate for a linearizing output. Such a process works very often. One may check that is works with example 5. The following example, due to Pierre Rouchon, shows that it is not always the case.

Example 6. -- We consider $L:=k\langle y_{1}, y_{2}\rangle$ and $K:=k\langle z_{1}, z_{2}\rangle$ such that the extension $K/L$ is associated to the differential prime ideal defined by characteristic set

$$z_{1}' = -{y_{1}''z_{1} + y_{2}' - y_{1}\over y_{1}'}$$ (1)

$$z_{2}' = -y_{1}'z_{1} + y_{2}..$$ (2)

We will illustrate on this example the algorithm deduced from the proof of theorem 3. We don't have in this case to introduce any equation for building $L$, which makes the example too simple. So let us modify it and take $L$ generated by $y_{1}, y_{2}, y_{3}$ with $y_{1}''=y_{3}$. In the same way, we replace $y_{1}''$ by $y_{3}$ in (1). We start with the set of equations:

$$y_{1}'z_{1}'+ y_{3}z_{1} + y_{2}' - y_{1} = 0$$ (3)

$$z_{2}' + y_{1}'z_{1} - y_{2} = 0$$ (4)

$$y_{1}'' - y_{3} = 0.$$ (5)

The Jacobi number for this system (in the variables $y$) is $2$ and its truncated jacobian matrice is:

$$J\llap{$\setminus$}:=\left(\matrix{0&1&z_{1}\cr z_{1}&1&0\cr... ...right)\quad\hbox{with}\quad \ell_{1}=0,\ell_{2}=1, \ell_{3}=0.$$

As $\ell_{2}=1$, we take the first derivative of (4), and reduce it using (3) and (5), getting:

$$z_{2}'' + y_{1}=0 .$$ (6)

We may replace equation (3) by equation (6), we get thus a system with Jacobi number $0$. The variable appearing with order $0$ in the equation (5) describing the extension $L/k$ is $y_{3}$ so the two remaining variables $y_{1}$ and $y_{2}$ form a linearizing output.

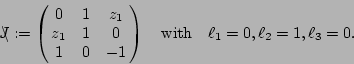
Remark 7. -- Using a variant of this algorithm, if we know a time varying linearizing output for a stationnary system, we can deduce a stationnary linearizing output (see [12] for this problem).