Proof of the main theorem

The proof uses Jacobi's bound for differential systems. This result introduced in [7] is still conjectural in the general case (see [10,3,4]). However, we can prove the following version using the effective construction given in [8].

Lemma 4. -- Let $P_{1}$, ..., $P_{n}$, $Q$ be polynomials in $k\{x_{1}, \ldots, x_{n}\}$ such that $P_{i}\notin(Q)$ and $[P]:Q^{\infty}$ is a prime differential ideal $I$ of differential dimension $0$. Let $e_{i,j}={\rm ord}_{x_{j}} P_{i}$,

$${\cal J}= \max_{\sigma\in S_{n}} \sum_{i=1}^{n} e_{i,\sigma(i)}$$

and

$$\vert J\llap{$\setminus$}\vert = \sum_{\sum_{i=1}^{n} e_{i,\... ...rtial P_{i}\over \partial x_{\sigma(i)}^{(e_{i,\sigma(i)})}},$$

i.e. we only keep in the jacobian matrix $(\partial P_{i}/\partial x_{j}^{(e_{i,j})})$ the products corresponding to the maximal sums of $e_{i,j}$.

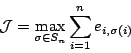
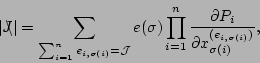
Then, the order of $I$ is equal to ${\cal J}$ if $\vert J\llap{$\setminus$}\vert\notin I$ and strictly lower than ${\cal J}$ if not.

The integer ${\cal J}$ is known as the Jacobi number and $\vert J\llap{$\setminus$}\vert$ is the truncated jacobian (determinans mancum in [7]). We denote by $\ell_{i}$ the minimal integers such that there exists a diagonal sum $\sum_{i=1}^{n} e_{\sigma(j),j}={\cal J}$ and for all $j\in[1,n]$ $e_{\sigma(j),j}$ is maximal among all $e_{i,j}+\ell_{i}$ (see [4,7]).

Sketch of the proof of theorem 3. -- In order to prove the theorem, we consider any algebraic extension $L_{2}/k$ and construct it as the quotient field of a prime differential ideal given by a characteristic set ${\cal A}$ in $k\{x_{1}, \ldots, x_{n}\}$. The extension $L_{2}\langle z\rangle/L_{2}$ is described by a prime differential ideal, whose characteristic set ${\cal B}$ admits a number of elements equal to $\hbox{\rm d.~tr.~deg.}\ L/k$.

Let $P$ be a set of $m$ equations such that $I=[S]:Q^{\infty}$, where $S:=P\cup{\cal A}$. Such a set $P$ exists, e.g. ${\cal B}$ satisfies the hypotheses if we take $Q=H_{\cal A}H_{\cal B}$. We may chose $L_{2}$, ${\cal A}$ and $P$ such that the bound ${\cal J}$ of lemma 4 is minimal. Now, we reorder the equations by increasing $\ell_{i}$, and for equal $\ell_{i}$, we take first the equations in ${\cal A}$. Let $j$ be the smallest integer such that the first $j$ rows of $J\llap{$\setminus$}$ are not of full rank. We will also assume that we have chosen $L_{2}$, ${\cal A}$ and $P$ with minimal $j$ among those with minimal ${\cal J}$.

Assume ${\cal J}\neq 0$. Then, as the extension is algebraic, the truncated jacobian $\vert J\llap{$\setminus$}\vert$ should be $0$; if not, the order of the extension would be ${\cal J}$. Now, if the truncated jacobian is $0$, we can construct by algebraic elimination a new set $P_{2}$ or a new extension $L_{2}$, associated with a new characteristic set ${\cal A}$ with a smaller ${\cal J}$, or an equal ${\cal J}$ and a smaller $j$. This contradicts minimality. So, ${\cal J}=0$ and $\vert J\llap{$\setminus$}\vert\neq0$.

This implies that there are $n-m$ variables $x_{i}$ appearing in ${\cal A}$ with order $0$ such that $\vert\partial A_{i}/\partial x_{j}\vert\neq0$ for $(i,j)\in[1,n-m]\times[m+1,n]$. We may assume those variables to be $x_{m+1}, \ldots, x_{n}$ after a reordering. This shows that $L_{2}/k\langle x_{1}, \ldots, x_{m}\rangle$ is algebraic, and so that $L/k$ is flat.    height .9ex width .8ex depth -.1ex

The proof is a constructive one. Provided that the extensions $L/k$, $K/L$ and $K/k$ are given by generators and relations, we are able, using characteristic sets computations, to construct a representation of $L/k$ as a flat extension. We investigate the algorithmic aspects of that theorem which reduce to a sequence of algebraic eliminations. If the computation could be in the worst case as difficult as algebraic elimination could be, we may very often in practice deduce some linearizing output from the parametrization without any elimination.

It should be noted that, if the flatness notion may be defined in a geometrical setting using ${\cal C}^{\infty}$ functions, the equations are most of the time polynomial in practice, making the algebraic definition, with its algorithmic potentialities, of special interest.