On va montrer comment l'on peut tester de manière rapide
l'observabilité et l'identifiabilité locale d'un système non
linéaire. Le résultat général est résumé par le théorème suivant, dû à
Alexandre Sedoglavic, en 2001. Dans l'énoncé qui suit, la borne de
complexité est obtenue, non à partir du degré des dénominateurs et des
numérateurs des fractions représentant les équations d'état, mais à
partir de leur complexité d'évaluation, c'est à dire du nombre
d'opérations élémentaires nécessaires pour les calculer. Ainsi
![]() se calcule en
se calcule en ![]() addition et
addition et ![]() multiplications,
c'est donc un polynôme de complexité
multiplications,
c'est donc un polynôme de complexité ![]() .
.
THÉORÈME 23. -- Considérons un modèle possédant ![]() variables d'état,
variables d'état, ![]() paramètres,
paramètres, ![]() sortie et
sortie et ![]() commandes. Supposons que les équations
de ce modèles soient représentées par un calcul d'évaluation de
complexité
commandes. Supposons que les équations
de ce modèles soient représentées par un calcul d'évaluation de
complexité ![]() .
.
Il existe un algorithme probabiliste qui distingue l'ensemble des variables observables et des paramètres identifiable du modèle, et qui indique le nombre de variable et de paramètres devant être supposés connus pour obtenir un modèle observable et identifiable.
La complexité arithmétique de cet algorithme est bornée par
Soient ![]() un entier positif arbitraire,
un entier positif arbitraire,
![]() et
et
L'idée de base de l'algorithme consiste à calculer un
développement en série de l'état ![]() , d'où l'on peut
déduire un développement en série des
, d'où l'on peut
déduire un développement en série des ![]() sorties
sorties
![]() . Ceci peut être fait de manière rapide par la méthode
de Newton. (Se reporter au cours 6 de Bruno Salvy (semaine 3),
théorème 4 p. 8.)
. Ceci peut être fait de manière rapide par la méthode
de Newton. (Se reporter au cours 6 de Bruno Salvy (semaine 3),
théorème 4 p. 8.)
Si le système est localement identifiable et observable, on peut
exprimer localement les ![]() fonctions d'état
fonctions d'état ![]() et les
et les ![]() paramètres
paramètres ![]() à partir des sorties
à partir des sorties ![]() et de leurs
dérivées. Il faut au plus aller jusqu'à l'ordre
et de leurs
dérivées. Il faut au plus aller jusqu'à l'ordre ![]() ,
qui borne l'ordre de dérivation
,
qui borne l'ordre de dérivation ![]() nécessaire. Sinon, on
à un système d'ordre inférieur en les sorties
nécessaire. Sinon, on
à un système d'ordre inférieur en les sorties ![]() , et les
dérivées suivantes des
, et les
dérivées suivantes des ![]() s'exprimerons à partir des
dérivées d'ordre inférieur à
s'exprimerons à partir des
dérivées d'ordre inférieur à ![]() . Elle
n'apporteront donc pas d'informations supplémentaires.
. Elle
n'apporteront donc pas d'informations supplémentaires.
Il suffit alors pour conclure de calculer le rang de la matrice
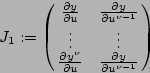
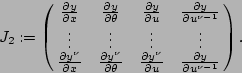
On calcule les rangs en remarquant que si ![]() est solution du système
1, alors
est solution du système
1, alors
![]() est
solution du sytème
est
solution du sytème
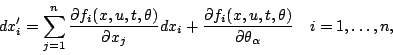
De même,
![]() est
solution du sytème
est
solution du sytème
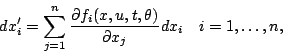
On obtient donc les développement en séries des solutions de ces équations par le même algorithme rapide, que pour le développement en série de l'état. (Il est difficile de dater l'idée d'utiliser ce type de système pour calculer les dérivées des solutions par rapports aux paramètres. On la trouve dans un cas particulier dans un article de Joseph Ritt en 1920. Le système linéarisé lui-même dans des papiers de Jacobi écrits vers 1850.)
L'aspect probabiliste consiste à choisir au hasard les valeurs
numériques correspondant aux fonctions d'état à ![]() , aux
paramètres, etc. Génériquement, les rang des matrices
seront ceux des expressions formelles. Il y a une probabilité
d'erreur qui peut être majorée en fonction de la taille des
nombre choisis pour les calculs.
, aux
paramètres, etc. Génériquement, les rang des matrices
seront ceux des expressions formelles. Il y a une probabilité
d'erreur qui peut être majorée en fonction de la taille des
nombre choisis pour les calculs.