Cinquième séance. Stabilisation par bouclage.

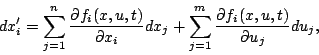
Nous avons vu comment identifier les paramètres d'un système et comment observer l'état. On a également montré comment résoudre les problèmes de planification de trajectoire pour des systèmes plats. Un difficulté subsiste: non seulement les valeurs des sorties sont bruitées, mais l'évolution du système elle-même dépend de « bruits», c'est-à-dire de perturbations inconnues. L'une d'elle, et non la moindre, est l'écart séparant le système physique «réel» du modèle simplifié utilisé pour bâtir le contrôle. Il faut donc être capable de corriger la trajectoire afin de la rapprocher de la trajectoire théorique.

Pour ce faire, on peut souvent utiliser le système linéarisé,

$$dx_{i}' =\sum_{j=1}^{n} {\partial f_{i}(x,u,t)\over\partial ... ...um_{j=1}^{m} {\partial f_{i}(x,u,t)\over\partial u_{j}}du_{j},$$

en supposant que l'écart $dx$ par rapport à la trajectoire de référence reste petit. Nous considérons le cas où l'on veut stabiliser le système au voisinage d'un point fixe.

On procède de la même manière que pour l'opérateur de Luenberger, mais cette fois, on va faire en sorte de construire un bouclage $u=Mx$, de manière à ce que la matrice $A + BM$ soit stable, c'est-à-dire ait toutes ses valeurs propres à partie réelle strictement négative. On montre de même que le polynôme caractéristique peut être construit arbitrairement pourvu que le système soit contrôlable. Il est inutile d'insister sur ce point.

Cependant, en général, on ne connaît pas l'état. Il faut donc le remplacer par la valeur ${\widehat x}$ recalculée par un observateur. Ceci nous conduit à poser $x'=Ax + BM_{1}{\widehat x}$, et ${\widehat x}'=A{\widehat x}+ BM_{1}{\widehat x} +M_{2}C({\widehat x}-x)$, en prenant pour $M_{1}$ la valeur voulue pour le bouclage et pour $M_{2}$ celle retenue pour l'observateur.

Plus généralement, on peut utiliser la platitude pour se ramener à une trajectoire donnée. Soit un système non-linéaire, $x'=f(x,u)$, pour lequel on dispose d'une sortie linéarisante $z$ (on considère encore par simplicité le cas à une commande). On veut suivre la trajectoire correspondant à $z=\phi(t)$. On va poser $P_{1}=(z-\phi(t))'-\lambda_{1}(z-\phi(t))$, ..., $P_{i}=P_{i-1}'-\lambda_{i}P_{i-1}$, etc. En prenant l'équation $P_{n}$, et en revenant dans les coordonnées $x$ de départ, on obtient un bouclage $x'=f(x,U(x))$, qui permet de se stabiliser au voisinage de la trajectoire voulue.

Ces méthodes nous permettent de garantir que, pour des perturbation assez petites, on restera au voisinage de la trajectoire ou du point de fonctionnement souhaité.