Contrôlabilité

DÉFINITION 3. -- Supposant connu le vecteur de paramètres $\theta$, on dit qu'un système différentiel est contrôlable (ou commandable) si pour tout état de départ $x_{0}$, tout état d'arrivée $x_{1}$, et tout temps fini non nul $T$ il existe une fonction de commande $u:[0,T]\mapsto {\bf R}$, telle que la solution du système 3 satisfaisant la condition initiale $x(0)=x_{0}$ satisfasse $x(T)=x_{1}$.

Ceci signifie concrètement que, connaissant l'entrée et la sortie, on peut recalculer l'état, sauf pour certaines trajectoires constituant un ensemble de mesure nulle. Cette propriété peut être testée par le critère de Kalman suivant.

THÉORÈME 4. -- Un système est commandable ssi la matrice

$$\left(\matrix{B & AB & \cdots & A^{n-1}B}\right)$$

est de rang $n$.PREUVE. -- Comme dans le cas de l'observabilité, le théorème de Cayley-Hamilton explique pourquoi il suffit de s'arrêter à $A^{n-1}B$. Pour simplifier, on va donner l'idée générale de la preuve dans le cas particulier où matrice $A$ est diagonalisable avec des valeurs propres toutes différentes et où il n'y a qu'une commande.

Sans restriction de généralité, on peut supposer être dans une base telle que $A$ soit diagonale. La matrice $\left(\matrix{B & AB & \cdots & A^{n-1}B}\right)$ est alors de rang $n$ ssi tous les $B_{i}$ sont non nuls. Supposons que $B_{i}=0$, alors $x_{i}(T)=x_{i}(0)e^{-\lambda_{i}T}$. On ne peut donc choisir arbitrairement l'état $x(T)$, ce qui contredit la contrôlabilité.

Réciproquement, on peut supposer par translation que la condition initiale est nulle. On a alors $x_{i}(1)=\int_{0}^{1} e^{\lambda_{i}(1-\tau)} u(\tau) d\tau$. Le plus simple, même si ce n'est pas très réaliste, est de prendre pour $u$ une combinaison linéaire de masses de Dirac $\sum_{i=1}^{n} c_{i}\delta_{i\lambda/n}$. On a alors $x(1) = M c$, où $M$ est une matrice de Vandermonde¹. Si les $\lambda_{i}$ sont tous différents entre eux, le déterminant de $M$ est non nul.    height .9ex width .8ex depth -.1ex

Si l'on prend par exemple pour $u$ un polynôme de degré $n-1$ dont les coefficients sont $c_{0}, \ldots, c_{n-1}$, on a $x(1) = M c$, avec

$$M_{i,j}=-e^{\lambda_{i}}\left(\lambda^{-1} + (j-1)\lambda^{-2} + \cdots + (j-1)!\lambda^{-j}\right) + (j-1)!\lambda^{-j},$$

en excluant le cas particulier $\lambda_{i}=0$. Le déterminant de $M$ est également non nul si les $\lambda_{i}$ sont tous différents, mais je ne sais pas le montrer directement. Ce sera une conséquence de l'approche par la notion de platitude qui sera introduite par la suite.

On peut envisager toutes sortes de lois de commande, pourvu qu'y interviennent un nombre suffisant de paramètres et que les rangs soient non nuls.

Un bon excercice est de compléter cette preuve dans un cadre plus général. Si l'on dispose d'un système de calcul formel, on peut en déduire une méthode de calcul d'une commande permettant d'aller de l'état $X_{0}$ à l'état $X_{1}$, c'est à dire de résoudre effectivement le problème de la planification de trajectoire. On verra bientôt une approche plus efficace.

Exemple 5. -- À l'extrême inverse, il faut envisager le cas où les $\lambda_{i}$ sont tous égaux à $0$. C'est par exemple celui d'un système en forme de Brunovský:

$$\begin{array}{lcl} x_{1}' &=& x_{2}\\ x_{2}' &=& x_{3}\\ x_{n}' &=& u. \end{array}$$

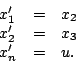
La planification de trajectoire se résoud alors simplement, puisque l'on peut exprimer $u$ en fonction de $x_{0}$: $u=x_{0}^{(n-1)}$

On a utilisé l'existence d'une solution explicite pour un système linéaire à coefficients constants. Dans des cas plus généraux, des solutions explicites existent rarement et sont souvent d'une taille décourageante. Mais on peut parfois avoir de la chance!

On peut de même, à titre d'exercice, mettre au point une preuve du critère d'observabilité reposant sur l'expression explicite de $x$ et en déduire une méthode de calcul de l'état.