Il s'agit d'une méthode très récente, introduite par Michel Fliess et Hebertt Sira-Ramìrez en 2002. L'idée de base a été découverte et décrite dans le cadre de la théorie des opérateurs de Mikusinski.
Elle permet d'identifier les paramètres, puis d'estimer
l'état. Elle converge pour des bruits ![]() dont la moyenne tend
vers
dont la moyenne tend
vers ![]() (
(
![]() tend vers
tend vers ![]() quand
quand ![]() tend vers l'infini), et permet d'émiminer des bruits «
structurés», solution d'équations différentielles
linéaires. Ceci est assez courant: bruit constant (défaut
d'étalonnage d'un capteur), sinusoïdal (parasitage par
l'alimentation électrique), etc.
tend vers l'infini), et permet d'émiminer des bruits «
structurés», solution d'équations différentielles
linéaires. Ceci est assez courant: bruit constant (défaut
d'étalonnage d'un capteur), sinusoïdal (parasitage par
l'alimentation électrique), etc.
Nous nous contenterons ici de présenter les principaux résultats dans un cadre simplifié, qui permet de se contenter d'un outillage mathématique réduit à l'intégration par partie.
Considérons un système de la forme
En posant ![]() , on se ramène alors à une équation de la forme
, on se ramène alors à une équation de la forme
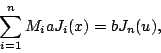 |
(7) |
Détailler les calculs est un excellent exercice et le plus sûr moyen de comprendre.
Ayant obtenu les ![]() , on peut ensuite calculer les
dérivées de
, on peut ensuite calculer les
dérivées de ![]() . En effet, si l'on multiplie seulement par
. En effet, si l'on multiplie seulement par
![]() , la
, la ![]() intégration fait apparaître un
terme dépendant de
intégration fait apparaître un
terme dépendant de ![]() , ce qui nous permet de le
calculer. Multipliant alors, par
, ce qui nous permet de le
calculer. Multipliant alors, par ![]() , on fait apparaître
, on fait apparaître
![]() et
et ![]() , d'où l'on déduit
, d'où l'on déduit ![]() etc.
etc.
Montrons brièvement comment on peut éliminer un bruit structuré,
solution de ![]() . Il suffit d'appliquer l'opérateur
. Il suffit d'appliquer l'opérateur ![]() aux deux
membres de l'équation (6), pour faire disparaître le
bruit. Reconstituer l'état suppose naturellement que les opérateurs
aux deux
membres de l'équation (6), pour faire disparaître le
bruit. Reconstituer l'état suppose naturellement que les opérateurs
![]() et
et
![]() soient sans
facteur commun.
soient sans
facteur commun.