Si l'on définit la contrôlabilité comme la possibilité d'atteindre en un temps fini arbitrairement bref, n'importe quel point de l'espace d'état à partir de n'importe quel point de l'espace, d'état, on est vite handicapé par une notion trop forte pour des systèmes non linéaires. Outre qu'elle excède de beaucoup ce que l'on souhaite faire en pratique, elle a le mauvais goût d'être indécidable, comme le montre la classe de systèmes suivant.
Exemple 15. -- À toute équation diophantienne
![]() , on
associe le système
, on
associe le système
Dès lors, tester la contrôlabilité pour tout système de cette forme reviendrait à pouvoir décider l'existence d'une solution pour une équation diophantienne (dixième problème de Hilbert), ce que l'on sait être impossible (Matyasevich 1970). (Je ne l'ai pas traité en cours, mais comme l'idée m'en vient, autant ne pas en priver les élèves intéressés.) On pourra bien sûr contester que cet exemple soit véritablement un système au sens de l'automatique: il est rare que l'on ait plus de commandes que de fonctions d'état.
On conçoit que ce type de préoccupation soit bien loin du monde de l'ingénieur qui leur préférera des notions plus pédestres. Il en existe beaucoup, et l'on se contentera d'extraire de ce bestaire l'accessibilité forte, qui nous semble la plus significative et la plus simple à énoncer comme à tester. Pour des systèmes non linéaires, on ne sait tester algorithmiquement que des notions locales.
DÉFINITION 16. -- Un système est fortement accessible si on peut atteindre en tout temps
![]() tous les points d'une boule ouverte de rayon strictement positif.
tous les points d'une boule ouverte de rayon strictement positif.
Un critère a été donné par Héctor J. Sussmann et
Velimir Jurdjevic en 1972. Rappelons que si ![]() et
et
![]() sont deux dérivations, leur crochet de Lie
sont deux dérivations, leur crochet de Lie
![]() , égal à
, égal à
![]() , est aussi une
dérivation. L'algèbre de Lie engendrée par un ensemble
, est aussi une
dérivation. L'algèbre de Lie engendrée par un ensemble ![]() de dérivations est le plus petit espace vectoriel stable par
crochet de Lie contenant
de dérivations est le plus petit espace vectoriel stable par
crochet de Lie contenant ![]() .
.
THÉORÈME 17. -- Un système est fortement accessible si, en tout point d'un ouvert
dense, l'algèbre de Lie ![]() engendrée par les dérivations
engendrée par les dérivations ![]() et
et
![]() (
(![]() ) est de dimension maximale
) est de dimension maximale
![]() .PREUVE. -- Pour prouver ce théorème, on peut utiliser le système linéarisé au
voisinage d'une trajectoire, défini par le système
.PREUVE. -- Pour prouver ce théorème, on peut utiliser le système linéarisé au
voisinage d'une trajectoire, défini par le système
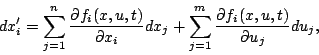
Sinon, l'algèbre de Lie ![]() est associée à un système d'EDP
linéaires qui possède, localement, des solutions non triviales. Le
nombre de solution
est associée à un système d'EDP
linéaires qui possède, localement, des solutions non triviales. Le
nombre de solution ![]() fonctionnellement indépendantes
(c'est-à-dire tel que l'on ne puisse trouver une fonction
fonctionnellement indépendantes
(c'est-à-dire tel que l'on ne puisse trouver une fonction ![]() non
identiquement nulle telle que
non
identiquement nulle telle que ![]() ) est égal
à la codimension de
) est égal
à la codimension de ![]() : elles définissent au voisinage de tout point
: elles définissent au voisinage de tout point
![]() de l'espace d'état une variété
de l'espace d'état une variété
![]() , où l'on
doit rester si l'on part de
, où l'on
doit rester si l'on part de ![]() . Ceci contredit l'accessibilité forte. height .9ex width .8ex depth -.1ex
. Ceci contredit l'accessibilité forte. height .9ex width .8ex depth -.1ex