Diffiétés

Nous nous efforçons de réduire au strict minimum l'appareil mathématique. Il est néanmoins utile d'introduire la notion de diffiété qui ne nécessite pas un effort considérable et permet de rendre plus accessible une partie de la littérature la plus récente qui l'utilise fréquement.

DÉFINITION 13. -- On appelle diffiété un ouvert $U$ de ${\bf R}^{I}$, muni de la topologie de Fréchet, où $I$ est dénombrable, équippé d'une dérivation (c'est-à-dire d'un champs de vecteur) $\delta$.

La topologie de Fréchet est la topologie la plus grossière telle que les projections sur ${\bf R}^{J}$, où $J\subset I$ est fini, soient continues.

On associe naturellement à un système de la forme 1 une diffiété $D\times \left({\bf R}^{{\bf N}}\right)^{m}\times {\bf R}$, où $D\subset{\bf R}^{n}$ est un ouvert correspondant aux valeurs admissibles pour les variables d'état. Un point de la diffiété est représenté par $(x_{1}, \ldots, x_{n}, u, u', \ldots, t)$. La dérivation $\delta$ correspond dans ce cas à

$${d\over dt}:= \sum_{i=1}^{n} f_{i}(x,u,t) {\partial\over\par... ...ial\over\partial u_{j}^{(\ell)}} + {\partial\over\partial t}.$$ (5)

Les fonctions définies sur la diffiétés sont des fonctions ${\cal C}^{\infty}$ d'un nombre fini de coordonnées. On note l'anneau de ces fonctions ${\cal O}(U)$. Un morphisme de diffiété $\phi:U\mapsto V$ est une application définie en coordonnées par des fonctions de ${\cal O}(U)$ et tel que $\delta_{V}\circ\phi=\phi\circ\delta_{U}$.

DÉFINITION 14. -- Une diffiété $U$ est plate s'il existe un ouvert $W$ dense dans $U$ tel que tout point de $W$ admette un voisinage isomorphe à un ouvert de l'espace des jets ${\rm J}^{\infty}({\bf R},{\bf R}^{m})$, qui peut être vu comme la diffiété $\left({\bf R}^{{\bf N}}\right)^{m}\times {\bf R}$, muni de la dérivation

$$\sum_{j=1}^{m}\sum_{\ell\in{\bf N}} z_{j}^{(\ell+1)}{\partial\over\partial z_{j}^{(\ell)}} + {\partial\over\partial t},$$

en écrivant les points de ${\rm J}^{\infty}({\bf R},{\bf R}^{m})$, sous la forme $(z_{1}, z_{1}', \ldots, z_{m}, z_{m}', \ldots, t)$

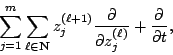
Cette définition est un peu plus précise et tient compte du fait qu'il existe souvent des points singuliers pour la platitude la platitude, au voisinage duquel on ne peut définir de paramétrage plat. Par exemple, pour la voiture, toutes les positions où celle-ci est immobile, puisqu'on ne peut alors déduire son orientation d'après la vitesse d'un point de l'essieu arrière.