jMEF

A Java library to create, process and manage mixtures of exponential families

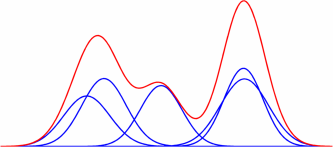
What are exponential families?

An exponential family is a generic set of probability distributions that admit the following canonical distribution: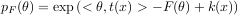

Exponential families are characterized by the log normalizer function F, and include the following well-known distributions:
Gaussian (generic, isotropic Gaussian, diagonal Gaussian, rectified Gaussian or Wald distributions, lognormal), Poisson, Bernoulli, binomial, multinomial, Laplacian, Gamma (incl. chi-squared), Beta, exponential, Wishart, Dirichlet, Rayleigh, probability simplex, negative binomial distribution, Weibull, von Mises, Pareto distributions, skew logistic, etc.
All corresponding formula of the canonical decomposition are given in the documentation
Mixtures of exponential families provide a generic framework for handling Gaussian mixture models (GMMs also called MoGs for mixture of Gaussians), mixture of Poisson distributions, and Laplacian mixture models as well.

What is jMEF?

jMEF is a Java cross-platform library developped by Vincent Garcia and Frank Nielsen. jMEF allows one to:

• create and manage mixture of exponential families (MEF for short),
• estimate the parameters of a MEF using Bregman soft clustering (equivalent by duality to the Expectation-Maximization algorithm),
• simplify MEFs using Bregman hard clustering (k-means algorithm in natural parameter space),
• define a hierachical MEF using Bregman hierarchical clustering,
• automatically retrieve the optimal number of components in the mixture using the hierarchical MEF structure.

A quick overview with slides.
A tutorial for the Matlab interface

Download jMEF and on line documentation

Download jMEF (jar) Download jMEF (sources) Documentation License.txt

Related bibliography

1. Vincent Garcia, Frank Nielsen, and Richard Nock
   Levels of details for Gaussian mixture models
   In Proceedings of the Asian Conference on Computer Vision, Xi'an, China, September 2009
   
   
2. Frank Nielsen, and Vincent Garcia
   Statistical exponential families: A digest with flash cards
   arXiV, http://arxiv.org/abs/0911.4863, November 2009
   
   
3. Frank Nielsen and Richard Nock
   Sided and symmetrized Bregman centroids
   IEEE Transactions on Information Theory, 2009, 55, 2048-2059
   
   
4. Frank Nielsen, Jean-Daniel Boissonnat and Richard Nock
   On Bregman Voronoi diagrams
   ACM-SIAM Symposium on Data Mining, 2007, 746-755
   
   
5. A. Banerjee, S. Merugu, I. Dhillon, and J. Ghosh
   Clustering with Bregman divergences
   Journal of Machine Learning Research, 2005, 6, 234-245
   
   

Tutorials

Bregman soft clustering

This tutorial reports the experiment proposed by Banerjee et al. in [5]. We create three 1-dimensional datasets of 1000 sample each, based on mixture models of Gaussian, Poisson and Binomial distributions, respectively. All the mixture models had three components with means centered at 10, 20 and 40, respectively. The standard deviation s of the Gaussian densities was set to 5 and the number of trials N of the Binomial distribution was set to 100 so as to make the three models somewhat similar to each other, in the sense that the variance is approximately the same for all three models. For each dataset, we estimate the parameters of three mixture models of Gaussian, Poisson and Binomial distributions using the proposed Bregman soft clustering implementation. The quality of the clustering was measured in terms of the normalized mutual information (Strehl and Ghosh, 2002) between the predicted clusters and original clusters (based on the actual generating mixture component). The results were averaged over 100 trials. This tutorial needs an additional file (k-means).

Download tutorial Download additionnal files

Parameter estimation of a mixture of Gaussian

This tutorial consists in the following steps:

1. We define a mixture f of univariate Gaussians of n components (e.g. n=3).
2. We draw m points from f (e.g. m=1000).
3. We estimate the parameters of a mixture f₁ of univariate Gaussians of n components using a classical expectation-maximization (EM) algorithm.
4. We estimate the parameters of a mixture f₂ of univariate Gaussians of n components using the Bregman soft clustering implementation (based on the duality of regular exponential families with regular Bregman divergences).

We then check that the estimated mixtures f₁ and f₂ are similar. This tutorial needs additional files.

Download tutorial Download additionnal files

Mixture model simplification with an application to image segmentation

This tutorial consists in the following steps:

1. Read an image file.
2. Load the correponding mixture of Gaussians (depending on the image and on the desired number number of components n) from a file. If the mixture doesn't exist yet, the mixture is estimated from the pixels of the image using Bregman soft clustering, and the mixture is saved in an output file.
3. Compute the image segmentation from the initial mixture model and save the segmentation result in an output file.
4. Simplify the mixture model in a mixture of m components.
5. Compute the corresponding image segmentation and save the segmentation result in an output file.

This tutorial needs additional files.

Download tutorial Download additionnal files

Fig. 1 - Application of mixture model simplification to image segmentation.

m=1	m=2	m=4	m=8	m=16	m=32

Hierarchical mixture models with an application to image segmentation

This tutorial consists in the following steps:

1. Read an image file.
2. Load the correponding mixture of Gaussians (depending on the image and on the desired number of components n) from a file. If the mixture doesn't exist yet, the mixture is estimated from the RGB pixels of the image using Bregman soft clustering, and the mixture is saved in an output file.
3. Compute the image segmentation from the initial mixture model and save the segmentation in an output file.
4. Compute a hierachical mixture model from the initial mixture model.
5. Extract a simpler mixture model of m components from the hierachical mixture model.
6. Compute the corresponding image segmentation and save the segmentation result in an output file.

Note that the hierachical mixture model allows to automatically extract the optimal number of components in the mixture model. To do this, use the method getOptimalMixtureModel(t) instead of getPrecision(m) in the tutorial. This tutorial needs additionnal files.

Download tutorial Download additional files

Fig. 2 - Application of hierarchical mixture models to image segmentation.

m=1	m=2	m=4	m=8	m=16	m=32

Statistical images

For this tutorial, we consider an input image as a set of pixels in a 5-dimensional space (color information RGB + position information XY). The mixture of Gaussians f is learnt from the set of pixels using the Bregman soft clustering algorithm. Then, we create two images (see Fig.3):

1. Each Gaussian is represented by an ellipse illustrating the mean (color + position) and the variance-covariance matrix (ellipse shape) (see row 2, Fig. 3).
2. Draw random points from f until at least 20 points per pixels have been drawn. Then, the color value of the statistical image pixel at the position (X,Y) is the average color value of the drawn points at the same position (see row 3, Fig. 3).

The proposed tutorial shows that the image structure can be captured into a mixture of Gaussians. The image is then represented by a small set of parameters (in comparison to the number of pixels) which is well adapted to applications such as color image retrieval. Considering an input image represented by its mixture of Gaussians, it is then trivial to retrieve, in a image database, a set of images have a similar color organization. This tutorial needs additionnal files.

Download tutorial Download additional files

Fig. 3 - Statistical images.

Original images
Gaussian representation
Statistical images

How to contribute to jMEF?

Please send requests, comments or criticisms to Vincent Garcia and Frank Nielsen. If you would like to add a particular distribution to the exponential family, send us:

• A TeX file describing the various formula corresponding to that exponential family,
• A corresponding Java file implementing those formula.

We give as an example the files corresponding to the multivariate Gaussian distributions:
MultivariateGaussian.java and MultivariateGaussian.tex.

MIT License

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

See details about MIT license.

The content on this site is licensed under a MIT License.