jMEF for Matlab

How to Use jMEF in Matlab

How to use jMEF in Matlab

Using jMEF in Matlab is pretty straightforward although there are a few things that you should care of

1. Make sure that jMEF.jar is in your javaclasspath, then import it.

   javaclasspath('D:\Work\jMEF.jar');
   import jMEF.*;
   

   Now, you can use jMEF in matlab, just try to create a simple GMM

   n=5;
   dim=4;
   mm=MixtureModel(n);
   mm.EF=MultivariateGaussian;
   
   for i=1:n
       mm.weight(i)=1/n;
       mm.param(i) = PVectorMatrix.RandomDistribution(dim);
   end
   

2. The java Enum type in Matlab R2009b and previous versions has a well known bug. In order to create an Enum type you have to use the following trick. This example tries to access the Enum type Clustering.CLUSTERING_TYPE which can take 3 values : LEFT_SIDED, RIGHT_SIDED, SYMMETRIC

   p=Clustering();
   classname=p.getClass.getClasses;
   MessageTypes = classname(1).getEnumConstants;
   

   MessageTypes(1) now contains the Enum LEFT_SIDED, MessageTypes(2) now contains the Enum RIGHT_SIDED and MessageTypes(3) now contains the Enum SYMMETRIC. You can now call a clustering method with your favorite centroid, for instance :

   symmetric_centroid=jMEF.Clustering.getCentroid(mm,MessageTypes(3));
   

3. /!\ Exponential families can be parametrized in three ways : SOURCE(MU,Sigma), NATURAL and EXPECTATION Parameters. For now, most functions from jMEF support all of the three types, however some of them do not. For instance EF.KLD (Kullback-Leibler Divergence) only accepts SOURCE parameters, and Clustering.Centroid methods only support NATURAL parameters. So when you want to modify or create parameters, or use one of the above functions, please check the doc and use the converting function accordingly (by the way, the type of parameters is also an ENUM so one can reuse the trick above to play with it)

   % Check my type (NATURAL, SOURCE, OR EXPECTATION)
   mm.param(1).type
   mm.param(2).type
   % The type is SOURCE, I can compute Kullback Leibler between those two.
   mm.EF.KLD(mm.param(1),mm.param(2));
   % I can also print the values, since it is the famous (MU,SIGMA)=(mean,covariance) Notation 
   mm.param(1)
   
   % If now, I need to call a centroid function which only supports NATURAL parameters.
   % Let us convert the parameters SOURCE->NATURAL 
   for i=1:n 
       mm.param(i)=mm.EF.Lambda2Theta(mm.param(i));
   end 
   % Now, I can call my centroid function 
   symmetric_centroid=jMEF.Clustering.getCentroid(mm,MessageTypes(3));
   % The result is in NATURAL paramters too
   % so if you want to print it with your favorite (MU,SIGMA) Notation, convert it NATURAL->SOURCE
   symmetric_centroid=mm.EF.Theta2Lambda(symmetric_centroid);
   

Demo 1: Estimate a centroid of a GMM

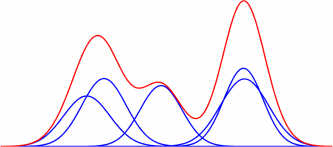
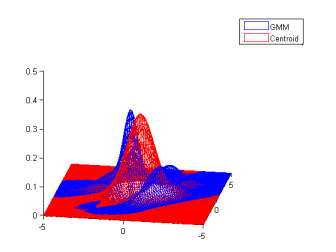
This is a demo of the wrapper, it loads jMEF (make sure you have jMEF.jar and that the javaclasspath is correct). Then it does some simple operations, creates a random GMM, compute its symmetrized bregman centroid (in this case Kullback-Leibler), then plot it.

Download Demo 1 (m)

Fig. 1 - Simple matlab demo, a random 2D GMM of 5 components and its symmetrized centroid, in red.

Demo 2 : Estimate a GMM from samples

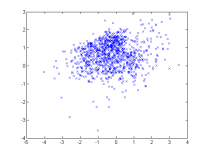
A simple demo, it draws 1000 random samples from a GMM and tries to estimate it using BregmanSoftClustering. It requires kmeans (contained in tools.jar).

Download Demo 2 (m) Required Package (.jar)

Fig. 2 - Draw random samples from a GMM (in blue), and try to estimate it using BregmanSoftClustering (in red).

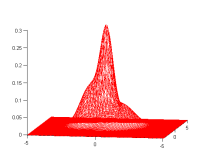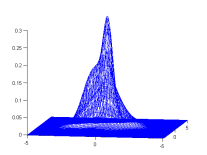
One random GMM	1000 samples from this GMM	GMM estimated from samples

			
Kullback Leibler divergence between original and estimated: 
 0.040888 
>>