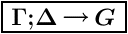
Lolli: A Linear Logic Programming Language
Based on the web page by Josh Hodas, written 26 July 1995. Recent
updates by Dale Miller.
Table of Contents
Introduction
Lolli is a logic programming language based on a fragment of linear
logic. As such it allows the programmer to exercise a significant
degree of control over the pattern of use of certain program clauses
(or resources) during proof search. The language was
designed by Josh Hodas and Dale
Miller and is described in the papers listed below.
Logic Programming in a Fragment of Intuitionistic Linear Logic,
by Joshua S. Hodas and Dale Miller, Information and
Computation, Vol. 110, No. 2, May 1, 1994, pp. 327-365. (DVI, Postscript).
Logic Programming in Intuitionistic Linear Logic: Theory,
Design, and Implementation, by Joshua S. Hodas, Ph.D. Dissertation from
University of Pennsylvania, Department of Computer and Information Science,
May 1994. Available as University of Pennsylvania Technical
Reports MS-CIS-92-28 or LINC LAB 269 (Postscript).
- Lolli: An Extension of
 Prolog with Linear Logic Context
Management, by Joshua S. Hodas, Proceedings of the 1992
Workshop on the
Prolog with Linear Logic Context
Management, by Joshua S. Hodas, Proceedings of the 1992
Workshop on the  Prolog Programming Language, Philadelphia, Summer
1992. Dale Miller, ed. (PDF).
Prolog Programming Language, Philadelphia, Summer
1992. Dale Miller, ed. (PDF).
See also: Overview
of linear logic programming, by Dale Miller.
Accepted as a chapter in the book Linear Logic in
Computer Science, edited by Thomas Ehrhard, Jean-Yves Girard,
Paul Ruet, and Phil Scott. Cambridge University Press.
(PostScript,
DVI,
PDF).
An older survey
article is also available.
Hodas has implemented a version of Lolli for version 0.93 of Standard ML of New Jersey and
released it in 1992. Version 0.701 of Lolli is available with the source code for the
interpreter and examples of Lolli sources.
It seems that the most active implementation effort on Lolli now is
being done on the language and compiler called LLP at Kobe University.
Motivations for the Development of Lolli
One way to understand Lolli is as a refinement of the logic of the
language  Prolog.
The language
Prolog.
The language
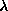 Prolog
extends the logic of horn clauses by allowing the use of implication
not just in clauses, but also in goals. (This is just one of several
significant ways that
Prolog
extends the logic of horn clauses by allowing the use of implication
not just in clauses, but also in goals. (This is just one of several
significant ways that
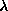 Prolog
extends Prolog. It also offers higher-order unification, arbitrarily
scoped quantifiers, and types, to name just a few of its features.)
The meaning of the goal
D
Prolog
extends Prolog. It also offers higher-order unification, arbitrarily
scoped quantifiers, and types, to name just a few of its features.)
The meaning of the goal
D
 G
is based on the bottom-up reading of the standard rule for proving an
implication formula in intuitionistic logic:
G
is based on the bottom-up reading of the standard rule for proving an
implication formula in intuitionistic logic:

That is, the system should first load the clause D into the
current program, and then try to prove the goal G using the
augmented program.
There are two important differences between implication goals in
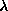 Prolog
and the use of
Prolog
and the use of assert in Prolog. First, whereas any logic
variables contained in a clause added using assert are
automatically closed with a universal quantifier, the variables in a clause
added using an implication are not. So, the interpreter must be prepared to
deal with live logic variables in the program. Second, regardless of whether
the goal G suceeds or fails, the assumed clause is discharged as soon
as the proof attempt is finished. Thus the assumption is scoped only over the
subordinate goal.
While the use of intuitionistic implications to augment the goal language
has been used to great success, two papers published in 1991 showed the
limitations of this approach:
Representing Objects in a Logic Programming Language with
Scoping Constructs, by Joshua S. Hodas and Dale Miller.
Proceedings of the Seventh International Conference on
Logic Programming, Jerusalem, June 1990. David H. D. Warren and
Peter Szeredi, eds. pp. 511-526 M.I.T. Press.
- Extending Definite Clause Grammars with Scoping Constructs,
by Remo Pareschi and Dale Miller. Proceedings of the Seventh
International Conference on Logic Programming,
Jerusalem, June 1990. David H. D. Warren and Peter Szeredi,
eds. pp. 373-389. M.I.T. Press.
(DVI, Postscript).
Related Systems
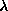 Prolog
is, as described above,
the parent of Lolli. It is based on the logic of Higher-Order Hereditary
Harrop Formulas, a fragment of ordinary (that is, not Linear) Intuitionistic
logic. It extends Prolog in two directions. The term language is extended
to allow arbitrary
Prolog
is, as described above,
the parent of Lolli. It is based on the logic of Higher-Order Hereditary
Harrop Formulas, a fragment of ordinary (that is, not Linear) Intuitionistic
logic. It extends Prolog in two directions. The term language is extended
to allow arbitrary
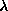 -terms
with full higher-order unification. The formula language is extended to allow
use of arbitrarily nested universal quantifiers and implications. The use of
the latter is described above.
-terms
with full higher-order unification. The formula language is extended to allow
use of arbitrarily nested universal quantifiers and implications. The use of
the latter is described above.
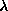 Prolog
was proposed and developed by
Dale Miller
and
Gopalan Nadathur.
Prolog
was proposed and developed by
Dale Miller
and
Gopalan Nadathur.
In order to determine whether a logic more expressive than Horn clauses
(the logic of Prolog) could still be seen as the foundation of a logic
programming language, Miller and Nadathur carefully analyzed the notion of
goal-directedness and made the following definition. A proof is goal directed
(or, in their words, uniform) if whenever a sequent has a non-atomic
formula as its right hand side (that is, as the goal) then the rule used
at that point is the one to decompose the goal. Logic programming, as distinct
from theorem proving, can be seen as the search for uniform proofs. A logic
is appropriate as a foundation of a logic programming language if uniform
proofs are complete for that logic.
This idea, in one form or another, underlies the design of all of the
languages mentioned here.
Lolli for
Alice is an implementation of Lolli in the functional
programming
language Alice that has
been used at the University of Edinburgh for Dialogue Planning.
Forum is an extension to Lolli. Unlike Lolli, and
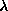 Prolog,
however, it is based on the multiple-conclusion (classical) system
rather than the intuitionistic one. Since there can be multiple goals
active at once, it is natural to think of Forum as representing a parallel
computation, rather than simply a sequential one.
Prolog,
however, it is based on the multiple-conclusion (classical) system
rather than the intuitionistic one. Since there can be multiple goals
active at once, it is natural to think of Forum as representing a parallel
computation, rather than simply a sequential one.
The design of Forum required extending the notion of Uniform Proof to
the multiple-conclusion setting. Miller made the natural choice, saying that
a multiple-conclusion proof is uniform if, when there is a non-atomic goal
on the right hand side, the last rule acts to decompose one such goal.
Further, for uniform proofs to be said to be complete, it must be that
any of the non-atomic goals could be decomposed at that point.
While Miller was guided by the notion of uniform proof in his design
of Forum, he was not designing a programming language. As such, goal directed
proofs (as defined by uniformity) only go so far. In particular, the language
allows one to provide a "program" clause that has the operator
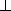 (one of Linear Logic's two falsehoods) as its head. Such a clause can
be used to backchain for any atomic goal. This will inevitably lead to
endless loops in any depth-first implementation. At present Miller, Hodas,
and Jeff Polakow are analyzing Forum to identify the fragment that makes sense
as a logic programming language. A preliminary implementation will be
available shortly.
(one of Linear Logic's two falsehoods) as its head. Such a clause can
be used to backchain for any atomic goal. This will inevitably lead to
endless loops in any depth-first implementation. At present Miller, Hodas,
and Jeff Polakow are analyzing Forum to identify the fragment that makes sense
as a logic programming language. A preliminary implementation will be
available shortly.
LO were the earliest proposals for a Linear Logic based
logic programming logic. Like Forum it is based on a
multiple-conclusion fragment of Linear Logic, and its design was
motivated by the desire to implement a parallel, object-oriented
language. The fragment of Linear Logic used is quite small. It
essentially extends Horn clauses by allowing the heads of clauses to
be formed not just of atoms, but of multisets of atoms joined by the
par operator. Thus LO execution can be seen as largely multi-set
rewriting. Linlog extends LO by adding several additional
operators. In fact, like Forum, the fragment is complete for Linera
Logic. It's operational flavor is determinde by a notion of
goal-directed proofs called Focusing Proofs which are closely
related to Uniform Proofs. LO and LinLog were proposed and developed
by Jean-Marc Andreoli and Remo Pareschi.
Lygon is a Linear Logic programming language based on a
fragment of multiple-conclusion (classical) linear logic. Like the
other languages described here the logic fragment that underlies the
language was chosen based on the requirement that uniform proofs (goal
directed proofs) be complete for that fragment. However, the
definition of uniform proof chosen differs from that used in the
design of Forum. In particular, whereas Forum requires that a sequent
be provable only if any non-atomic formula on the right hand
side can be selected for decomposition, Lygon requires only that
some such formula be selectable. Lygon was first proposed by
James Harland and David Pym.
An Annotated Bibliography
- Theory, Design, and Implementation of Lolli:
- Logic Programming in a Fragment of Intuitionistic Linear Logic:
Extended Abstract,
by Joshua S. Hodas and Dale Miller,
Proceedings of the Sixth Annual Symposium on
Logic in Computer Science,
Amsterdam, July 1991. Gilles Kahn, ed. IEEE Computer Society Press.
The first paper in which the motivations for and design of Lolli
were presented. This paper was rewritten and significantly expanded
(including a much clearer presentation of the logic)
for the following paper, and should be read only for historical
interest.
- Logic Programming in a Fragment of Intuitionistic Linear Logic,
by Joshua S. Hodas and Dale Miller,
Information and Computation, Vol. 110, No. 2, May 1, 1994,
pp. 327-365.
An extended and rewritten version of the previous paper, this one lays
out the motivations for developing Lolli, then details the logic and
meta-theory of the language, and finally presents a series of examples of
its use.
-
Logic Programming in Intuitionistic Linear Logic:
Theory, Design, and Implementation,
by Joshua S. Hodas,
Ph.D. Dissertation from
University of Pennsylvania, Department of Computer and Information Science,
May 1994. Available as University of Pennsylvania Technical
Reports MS-CIS-92-28 or LINC LAB 269.
Hodas' dissertation can be viewed as a greatly expanded version of the
Information and Computation paper. The logic and meta-theory are presented in
detail with full proofs; more and longer examples are given, and the
implementation of the language is discussed at length. Also included are a
presentation of a more optimized (less non-deterministic) version of the
operational semantics of Lolli (this is the semantics of the first public
release of the language), as well as a proposed extension of Lolli to allow
direct specification of the Affine and Relevant constarints.
- Lolli: An Extension of
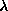 Prolog
with Linear Logic Context Management, by Joshua S. Hodas,
Proceedings of the 1992 Workshop on the
Prolog
with Linear Logic Context Management, by Joshua S. Hodas,
Proceedings of the 1992 Workshop on the 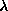 Prolog Programming
Language, Philadelphia, Summer 1992. Dale Miller, ed.
Prolog Programming
Language, Philadelphia, Summer 1992. Dale Miller, ed.
This short paper is a good introduction to the logic and syntax of
Lolli, particularly for those already familiar with
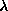 Prolog.
Prolog.
- Applications of Lolli:
- This paper presents a more complete description of our treatment
of Generalized Phrase Structure Grammar in Lolli. It is self-contained,
including a brief introduction to Lolli. The material was presented again
in somewhat nicer notation with a few more details worked out in Hodas'
dissertation.
Specifying Filler-Gap Dependency Parsers in a Linear-Logic
Programming Language,
by Joshua S. Hodas,
Proceedings of the 1992 Joint International Conference and Symposium on
Logic Programming,
Washington D.C., November 1992. Krystopf Apt, ed. MIT Press.
- Extensions of Lolli:
- This paper presents a variant of the logic of Lolli in which it
is possible to directly specify the Relevant (clauses may be copied but
not discarded) and Affine (clauses may be discarded but not copied)
constraints. Examples are given showing the usefulness of the extension.
Logic Programming with Multiple Context Management Schemes,
by Joshua S. Hodas,
Proceedings of the Fourth International Workshop on Extensions of
Logic Programming,
St. Andrews, Scotland, March/April 1993. Roy Dyckhoff, ed.
Springer-Verlag Lecture Notes in Artificial Intelligence 798, 1994.
Validate
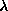 Prolog with Linear Logic Context
Management, by Joshua S. Hodas, Proceedings of the 1992
Workshop on the
Prolog with Linear Logic Context
Management, by Joshua S. Hodas, Proceedings of the 1992
Workshop on the 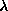 Prolog Programming Language, Philadelphia, Summer
1992. Dale Miller, ed. (PDF).
Prolog Programming Language, Philadelphia, Summer
1992. Dale Miller, ed. (PDF).
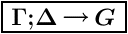
 G
is based on the bottom-up reading of the standard rule for proving an
implication formula in intuitionistic logic:
G
is based on the bottom-up reading of the standard rule for proving an
implication formula in intuitionistic logic:

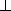 (one of Linear Logic's two falsehoods) as its head. Such a clause can
be used to backchain for any atomic goal. This will inevitably lead to
endless loops in any depth-first implementation. At present Miller, Hodas,
and Jeff Polakow are analyzing Forum to identify the fragment that makes sense
as a logic programming language. A preliminary implementation will be
available shortly.
(one of Linear Logic's two falsehoods) as its head. Such a clause can
be used to backchain for any atomic goal. This will inevitably lead to
endless loops in any depth-first implementation. At present Miller, Hodas,
and Jeff Polakow are analyzing Forum to identify the fragment that makes sense
as a logic programming language. A preliminary implementation will be
available shortly.