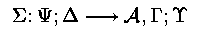
Contents: [Design goals | Applications | Implementations | References]
Forum is a presentation of all of higher-order linear logic that makes it into a logic programming language. The main references for this paper are [Miller 1996, Miller 1994, Chirimar 1995]. The survey paper A Survey of Linear Logic Programming may also be of interest.
The sequent calculus proof system that defines Forum is contained in this GIF file: this is taken from [Miller 1996].
The description of logic programming above is based on single-conclusion sequents: that is, on the right of the sequent arrow in Sigma : Delta --> G is a single formula. A natural generalization requires that all possible introductions on the right can be done simultaneously. Although the sequent calculus cannot deal directly with simultaneous rule application, reference to permutabilities of inference rules can indirectly address simultaneity. That is, we can require that if two or more right-introduction rules can be used to derive a given sequent, then all possible orders of applying those right-introduction rules can, in fact, be done and the resulting proofs are all equal modulo permutations of introduction rules. Forum was the result of applying this definition to linear logic.
A sequent proof system for intuitionistic logic was represented in [Miller 1996]. The meta-theory of linear logic was used to transform that sequent system into a natural deduction proof. Using Forum as a logical framework for both sequent calculus and natural deduction seems to be a promising line of research.
In [Chirimar 1995], the sequential and pipled semantics of the DLX risc-processor were specified and shown to be formally correct.
Several specifications of the operational semantics of programming languages have been written in Forum. In [Miller 1996] the semantics of an Algol-like notion of references was given, as was the concurrency primitives of Concurrent ML. In [Chirimar 1995], many of the imperative features of Standard ML (references, exceptions, continuations) were specified and used to prove equivalences of code phrases.
A group at the University of Genova, including Maurizio Martelli and Giorgio Delzanno, have written some papers where they specify various object-oriented programming language constructs in Forum. Delzanno has implemented (in lambda Prolog an interpreter for an object-oriented programming language that uses Forum fordescribing its operational semantics.
Christian Urban (now at Cambridge University) has written a MPhil at St. Andrews titled Forum and its Implementation (abstract). The full thesis is available from Urban. This thesis contains various examples of using Forum as well as a new calculus for the management of resources in proof search. His implementation of Forum is mentioned below.
Manuel Chakravarty has written a PhD at the Technische Universität of Berlin titled On the Massively Parallel Execution of Declarative Programs (an abstract and postscript are available). In this thesis, he uses Forum to specify the operational semantics of a parallel programming language that combines functional and logic programming paradigms.
There are many reason why Forum, as it is defined in the papers above, cannot seriously be implemented directly with the hope of turning specifications into prototype implementations.
Forum allows arbitary higher-order quantification. In particular, there are no restrictions on how predicates can be quantified. As a result, unification (even higher-order unification) will not produce all the substitutions that might be necessary for predicate variables. An easy way to convenience yourself of this is to write done the partial correctness statement of some looping program as a second-order formula (the invariant of the loop would be the substitution for a predicate variable). This formula will probably be in intuitionistic logic and hence can be mapped into Forum without trouble. It would be too much to ask of an interpreter to find loop invariants!
Forum allows clauses to have ``multi-heads''. If this head has one atom in it, then it can be used in a manner similar to how clauses are used in backchaining in Prolog and lambda Prolog. If this head has more than atom, then a kind of n-way synchronization (n>1) is needed. Synchronizations of this kind can be managed using multiset rewriting techniques, but, in general, such synchronization is expensive. To convince yourself of this, write down in Forum a simple solution to the Dining Philosophers Problem. However, the really difficult thing about Forum is that it allows clauses to have no atoms in their head. Such 0-way synchronization has some pretty logical uses, but it would lead a naive interpreter into a tight and endless loop.
Even if quantification of predicate variables would be removed, Forum also allows for quantification at higher-order types over terms. It is this feature, also found in lambda Prolog and Isabelle that allows for an elegant treatment of bound variables and object-level substitution, a treatment often referred to as higher-order abstract syntax. In the presence of simply typed lambda-terms and such quantification, higher-order unification is required in an interpreter. Such unification has some nasty properties, such as undecidability and possibility infinite numbers of incomparable unifiers.
Predicate quantification can be removed or greatly restricted. In lambda Prolog, for example, such quantification is allowed (its presence provides a natural approach to doing higher-order programming in logic) but restricted so that predicate variables do not in certain locations. In the resulting language, unification does compute all the necessary substitutions. The example involving loop invariances not possible with such restrictions. Many of the applications of Forum do not use predicate quantification.
Empty headed clauses probably need to be disallowed, except, possibly, when appear in the linear context and can only be used once (avoiding a loop in constantly reusing them).
Again the experience with lambda Prolog is relevant here: a large set of example specifications do not use, in fact, full higher-order quantification but, rather, a small subset that requires only higher-orde pattern unification (also called L-lambda unification) and such unification resembles first-order unification significantly while still providing a natural treatment of higher-order abstract syntax.
Thus, it would seems that if the full Forum was restricted in these various ways, an interesting and useful logic would result that might yield useful prototypes.
A lambda Prolog implementation. Making only the restriction mentioned in point (1) above, it was possible to take the transition system in [Miller 1996] and specify it directly in lambda Prolog. The result is a naive and grossly inefficient interpeter for Forum, adequate only to test some particularly simple examples. Below the modules one.mod and two.mod provide examples of just such a specification. These interpreters can be used to interpret certain small Forum specification examples.
University of Málaga implementation. UMA Forum is an implementation in Prolog of a subset of Forum. It is being used as part of a research project concerning linear logic, logic programming, object orientedness and concurrency. Being a research programming language, most of UMA Forum features are subject to change; although it intends to be an efficient implementation of a large portion of Forum. Developed by Pablo Lopez and Ernesto Pimentel.
St. Andrews implementation. Christian Urban has written a MPhil at St. Andrews titled Forum and its Implementation (abstract). The full thesis is available from Urban. His implementation of an interpreter is available here.
An SML implementation.Many of the problems of providing an effective implementation of some subset of Forum are being addressed in implementation effort of Lolli. Josh Hodas and his students have been working on implementation of both Lolli and Forum in ML. For more information on this system, please send mail to Josh Hodas.
[Andreoli & Pareschi 1991] J.-M. Andreoli and R. Pareschi. Linear objects: Logical processes with built-in inheritance. New Generation Computing, 9:445-473, 1991.
[Chirimar 1995] J. Chirimar. Proof Theoretic Approach to Specification Languages. PhD thesis, Department of Computer and Information Science, University of Pennsylvania, 1995. Available in PostScript format.
[Hodas & Miller 1994] J. S. Hodas and D. Miller. Logic programming in a fragment of intuitionistic linear logic. Information and Computation, 110(2):327-365, 1994. Extended abstraction in the Proceedings of the Sixth Annual Symposium on Logic in Computer Science, Amsterdam, July 15-18, 1991. Available in DVI and PostScript formats.
[Miller et. al. 1991] D. Miller, G. Nadathur, F. Pfenning, and A. Scedrov. Uniform Proofs as a Foundation for Logic Programming. Annals of Pure and Applied logic, 51:125-157, 1991. Available in DVI. An abstract and errata are also available.
[Miller 1994] D. Miller. A multiple-conclusion meta-logic. In S. Abramsky, editor, Ninth Annual Symposium on Logic in Computer Science, pages 272-281, Paris, France, July 1994. IEEE Computer Society Press. Available in PostScript format.
[Miller 1996] D. Miller. A Multiple-Conclusion Meta-Logic. Theoretical Computer Science 165(1): 201-232 (1996). (DVI) (Abstract).
This material is based upon work supported by the National Science Foundation under Grant No. 9896139.