5. Le groupe du Tas de sable.

Afin de comprendre cet espace de configuration il est utile de comprendre et de calculer la structure du groupe.
Nous nous intéresserons ici à la décomposition de Smith d'un groupe.

Cette décomposition donne tout groupe abélien fini comme un produit direct de sous-groupes cycliques de cardinaux d₁ , d₂ , ... , d_n tels que d₁ | d₂ | ... | d_n.

Il y a de nombreuses méthodes pour calculer les formes de Smith d'un groupe. Pour plus de renseignements sur ce sujet se référer au livre A Course In Computational Algebraic Number Theory de Henri Cohen .

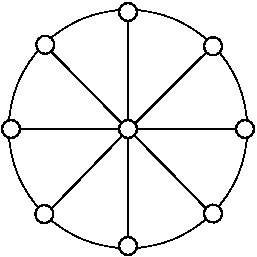
Néanmoins on peut démontrer que pour le graphe roue

la forme de Smith peut s'écrire comme un produit de deux groupes cycliques

• Dans le cas ou le nombre n de points sur le pourtour de la roue est pair, alors le gorupe est produit de deux sous groupes de cardinaux 5 f_nn.
• Dans le cas impair alors on a un produit de deux sous-groupes de même ordre f_n-1 + f_n+1

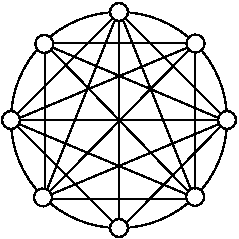
Cas du graphe Complet K_n