suivant: À propos de ce
Un système d'équations différentielles ordinaires est non canonique3 si les plus hautes dérivées des variables dépendantes apparaissent dans les équations de telle manière qu'on ne puisse en déduire leur valeur. Ce qui fait que chaque fois l'on trouve des équations indépendantes de ces dérivées les plus hautes, soit dans le système lui-même, soit à partir de lui par élimination. Dans ce cas, le nombre de constantes arbitraires que fait intervenir une intégration complète -- soit l'ordre du système -- est toujours inférieur à la somme des ordres les plus hauts jusqu'où montent les dérivées de chacune des variables dans le système considéré.4 On connaît l'ordre du système, si on arrive par différentiations et éliminations à une forme canonique équivalente, de sorte que l'on puisse revenir du système canonique au système considéré. Car la somme des ordres les plus hauts jusqu'où montent dans le système canonique les dérivées de chaque variable dépendante sera aussi l'ordre du système non canonique. Mais pour trouver cet ordre, la réduction à une forme canonique n'est pas nécessaire : la chose peut aussi être résolue par les considérations suivantes.
Supposons
que l'on ait entre la variable indépendante ![]() et les
et les ![]() variables
dépendantes
variables
dépendantes ![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() équations
différentielles
équations
différentielles
En recherchant l'ordre du
système d'équations différentielles
linéaires (2), on peut supposer que les
coefficients sont constants6. Dans ce cas, on obtient une intégration
complète par une méthode bien connue, sans faire aucune
réduction en forme canonique. Nous désignons par le symbole :
Éliminant
![]() , on obtient une équation
algébrique dont les racines produisent les valeurs que peut
prendre
, on obtient une équation
algébrique dont les racines produisent les valeurs que peut
prendre ![]() , et à chaque racine ou valeur de
, et à chaque racine ou valeur de ![]() correspond un système de valeurs
correspond un système de valeurs
![]() que
l'on peut toutes multiplier par une même constante arbitraire. En
sommant les valeurs de chaque variable
que
l'on peut toutes multiplier par une même constante arbitraire. En
sommant les valeurs de chaque variable ![]() correspondant à
toutes les racines, on obtient sa valeur complète, et comme les valeurs
de chaque variable ainsi obtenues sont pourvues des mêmes
constantes arbitraires, l'intégration complète de
l'équation (5) induit autant de constantes
arbitraires qu'il y a de valeurs de
correspondant à
toutes les racines, on obtient sa valeur complète, et comme les valeurs
de chaque variable ainsi obtenues sont pourvues des mêmes
constantes arbitraires, l'intégration complète de
l'équation (5) induit autant de constantes
arbitraires qu'il y a de valeurs de ![]() . Donc, l'ordre du
système d'équations linéaires (2), ou celui
du système différentiel considéré (1)
sont égaux au degré de l'équation algébrique qui
définit
. Donc, l'ordre du
système d'équations linéaires (2), ou celui
du système différentiel considéré (1)
sont égaux au degré de l'équation algébrique qui
définit ![]() . On peut représenter cette équation de la
manière suivante
. On peut représenter cette équation de la
manière suivante
Proposition I. Soient ![]() équations différentielles entre
la variable indépendante
équations différentielles entre
la variable indépendante ![]() et les variables
dépendantes
et les variables
dépendantes
![]()
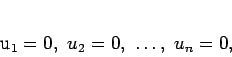
Dans ce qui précède, j'appelle maximum une valeur non
inférieure à celle d'aucune autre somme, de sorte que plusieurs
maxima égaux entre eux peuvent avoir lieu correspondant à divers
indices
![]() du système.
du système.
Le degré de l'équation algébrique (7) ne
diminue pas, sauf si dans le déterminant de droite le coefficient de
la plus grande puissance de la quantité ![]() s'annule.
s'annule.
Nous obtiendrons d'autre part le coefficient de la plus haute des
puissances de ![]() si, en formant le déterminant, nous
substituons à chaque fonction rationnelle
entière
si, en formant le déterminant, nous
substituons à chaque fonction rationnelle
entière
![]() le coefficient de la plus haute,
c'est-à-dire de la
le coefficient de la plus haute,
c'est-à-dire de la ![]()
![]() puissance que je désignerai
par
puissance que je désignerai
par
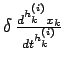 provenant
de la variation de la fonction
provenant
de la variation de la fonction ![\begin{displaymath}[c]_{h_{k}^{(i)}} = \frac{\partial u_{i}}{\displaystyle\partial\,
\frac{{d}^{h_{k}^{(i)}}x_{k}}{{d}t^{h_{k}^{(i)}}}}.
\end{displaymath}](img65.png)
Proposition II. On appelle ![]() la dérivée partielle de
la dérivée partielle de ![]() prise selon la plus haute des dérivées de
prise selon la plus haute des dérivées de ![]() que contient
la fonction
que contient
la fonction ![]() (i.e. d'ordre
(i.e. d'ordre ![]() ). De tous les
termes du déterminant
). De tous les
termes du déterminant
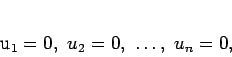
Nous obtenons par ce qui précède un nouveau genre de formules, les
déterminant tronqués
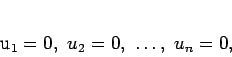
En cherchant l'ordre d'un système d'équations différentielles quelconques, une voie consiste à trouver une méthode par laquelle leur réduction en forme canonique puisse être effectuée10. Mais dans cet article, qu'il nous suffise de rechercher avec soin la nature du maximum dont il est question et comment on peut le trouver aisément.
Par ce qui précède, la recherche de l'ordre d'un système d'équations différentielles ordinaires est ramené au problème d'inégalités suivant, également digne d'être considéré pour lui-même :
Les quantités ![]() étant disposées en une figure carrée
étant disposées en une figure carrée
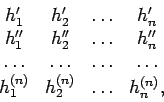
Faisons en sorte que les quantités ![]() ,
,
![]() ,
...,
,
..., ![]() soient ainsi déterminées, que les
quantités
soient ainsi déterminées, que les
quantités ![]() étant disposées en carré de la même
manière que les quantités
étant disposées en carré de la même
manière que les quantités ![]() et que choisissant un
maximum dans chaque série verticale, ces maxima se trouvent dans des
séries horizontales toutes différentes. Si on
appelle
et que choisissant un
maximum dans chaque série verticale, ces maxima se trouvent dans des
séries horizontales toutes différentes. Si on
appelle
![]() le maximum des termes
le maximum des termes
Par
brièveté, j'appellerai canon une figure carrée dans laquelle les
maxima des diverses séries verticales sont dans des séries
horizontales toutes différentes. Il est clair que dans un tel
canon, on peut augmenter ou diminuer tous les termes d'une
même quantité, d'où il s'en suit que parmi les
quantités
![]() une ou
plusieurs peuvent être rendues égales à
une ou
plusieurs peuvent être rendues égales à ![]() , les autres étant
positives. Si
, les autres étant
positives. Si ![]() , la séries
, la séries ![]() ,
, ![]() ,
...,
,
..., ![]() est la même que la série
d'origine
est la même que la série
d'origine
![]() , c'est
pourquoi j'appellerai série inchangée une série du
canon qui correspond à une quantité
, c'est
pourquoi j'appellerai série inchangée une série du
canon qui correspond à une quantité ![]() nulle. Parmi toutes les
solutions, il y en aura une la plus simple, en ce sens que les
quantités
nulle. Parmi toutes les
solutions, il y en aura une la plus simple, en ce sens que les
quantités ![]() prendront des valeurs minimales, de sorte qu'on
n'en trouvera pas d'autre pour laquelle certaines des
quantités
prendront des valeurs minimales, de sorte qu'on
n'en trouvera pas d'autre pour laquelle certaines des
quantités ![]() prendront des valeurs inférieures, les autres
restant inchangées. J'appellerai le canon correspondant à cette
solution un canon le plus simple. Il en sera
question dans ce qui suit.
prendront des valeurs inférieures, les autres
restant inchangées. J'appellerai le canon correspondant à cette
solution un canon le plus simple. Il en sera
question dans ce qui suit.
À un tableau carré quelconque, j'associe les dénominations
suivantes, qui sont à bien retenir : par série,
j'entendrai toujours une série horizontale ; s'il s'agit
d'une série verticale, cela sera précisé. Par maximum,
j'entendrai toujours un terme maximal parmi tous ceux de la même
verticale, ou qui n'est inférieur à aucun autre.
J'appellerai donc maximum d'une série, un terme d'une
série horizontale qui est maximal parmi tous ceux placés dans la
même verticale que lui. Il peut arriver qu'une série n'ait aucun
maximum ou plusieurs différents entre eux. Et si la figure est
constituée comme un canon, chaque série jouit assurément d'un
maximum, car si plusieurs sont présents dans la même série, on
peut toujours sommer de manière que tous les maxima des diverses
séries appartiennent à des verticales différentes,
c'est-à-dire qu'ils forment un système complet de maxima
transversaux. Nous considérons dans le canon le plus simple le
système de ces maxima, et s'il s'en présentent plusieurs de cette
sorte, nous en choisissons un quelconque. Nous distribuons alors
toutes les séries en deux parties: les séries ![]() et les séries
et les séries ![]() ,
de telle sorte qu'aucune des séries de
,
de telle sorte qu'aucune des séries de ![]() ne soit inchangée,
c'est-à-dire qu'aucune des quantités
ne soit inchangée,
c'est-à-dire qu'aucune des quantités ![]() qui correspondante aux
séries
qui correspondante aux
séries ![]() ne s'annule. Je dis qu'on a
ne s'annule. Je dis qu'on a
Théorème I. Dans le canon le plus simple, au moins
l'un des maxima des séries ![]() est égal à un terme situé
dans la même verticale et appartenant à une série
est égal à un terme situé
dans la même verticale et appartenant à une série ![]() .
.
Autrement, on pourrait diminuer toutes les quantités ![]() relatives
aux séries
relatives
aux séries ![]() d'une même quantité jusqu'à ce que l'une des
quantités
d'une même quantité jusqu'à ce que l'une des
quantités ![]() s'annule ou que l'un des maxima des séries
s'annule ou que l'un des maxima des séries ![]() égale un terme placé sur la même verticale et appartenant à
une série
égale un terme placé sur la même verticale et appartenant à
une série ![]() . En effet, jamais ainsi les maxima des diverses
séries ne cesseront d'être des maxima, ni la structure du canon ne
sera perturbée. Alors, les quantités
. En effet, jamais ainsi les maxima des diverses
séries ne cesseront d'être des maxima, ni la structure du canon ne
sera perturbée. Alors, les quantités ![]() proposées ne seraient
pas des valeurs positives minimales ni le canon le plus simple.
proposées ne seraient
pas des valeurs positives minimales ni le canon le plus simple.
Si les séries ![]() se résument à une seule série, le théorème précédent
implique cet autre.
se résument à une seule série, le théorème précédent
implique cet autre.
Théorème II. Dans un canon le plus simple, le maximum d'une série non inchangée est égal à un autre terme de la même verticale
Étant donné un canon le plus simple, nous choisissons de nouveau un
système complet de maxima transversaux. Dans une
série ![]() quelconque, à laquelle correspond une
quantité
quelconque, à laquelle correspond une
quantité ![]() non nulle, se trouve un maximum auquel est
égal selon
non nulle, se trouve un maximum auquel est
égal selon ![]() un terme dans la même verticale appartenant à
une série
un terme dans la même verticale appartenant à
une série ![]() où se trouve de nouveau un maximum
qui est égal à un terme de la même verticale d'une
série
où se trouve de nouveau un maximum
qui est égal à un terme de la même verticale d'une
série ![]() , et ainsi de suite. Si à un maximum
donné sont égaux plusieurs termes de la même verticale, le
processus décrit peut être mené de plusieurs manières mais on
a
, et ainsi de suite. Si à un maximum
donné sont égaux plusieurs termes de la même verticale, le
processus décrit peut être mené de plusieurs manières mais on
a
Théorème III. Dans le canon le plus simple, parmi les diverses manières d'aller
d'une série donnée à une autre par le processus décrit, il
s'en trouve toujours une par laquelle on parvient à une série
inchangée i.e. une série à laquelle correspond la
valeur ![]() .
.
Car, si le théorème ![]() n'a pas lieu, on divise les séries du
canon en deux ensembles12 dont le premier contient toutes les
séries qu'on peut atteindre par le processus donné et le second
toutes celles qu'on ne peut pas atteindre, de sorte que les séries
inchangées sont toutes dans le second ensemble. Ce faisant, on peut
prendre le premier ensemble pour les séries
n'a pas lieu, on divise les séries du
canon en deux ensembles12 dont le premier contient toutes les
séries qu'on peut atteindre par le processus donné et le second
toutes celles qu'on ne peut pas atteindre, de sorte que les séries
inchangées sont toutes dans le second ensemble. Ce faisant, on peut
prendre le premier ensemble pour les séries ![]() et le second pour
les séries
et le second pour
les séries ![]() du théorème
du théorème ![]() . Donc, selon le
théorème
. Donc, selon le
théorème ![]() , on peut aller d'une série du premier ensemble à
une série du second, ce qui est contre l'hypothèse. D'où
l'absurdité de la supposition que le théorème
, on peut aller d'une série du premier ensemble à
une série du second, ce qui est contre l'hypothèse. D'où
l'absurdité de la supposition que le théorème ![]() n'a pas
lieu.
n'a pas
lieu.
Par brièveté, j'appellerai par la suite
canon
![]() un canon
quelconque où les quantités
un canon
quelconque où les quantités
![]() , que je suppose toujours positives ou nulles, prennent
respectivement la place de
, que je suppose toujours positives ou nulles, prennent
respectivement la place de
![]() . Ceci défini, nous aurons à propos de ces deux canons
le
. Ceci défini, nous aurons à propos de ces deux canons
le
Théorème IV. Deux canons étant donnés, le premier ![]() ,
,
![]() , ...,
, ..., ![]() , le second
, le second ![]() ,
,
![]() , ...,
, ..., ![]() , il y aura toujours un autre
canon
, il y aura toujours un autre
canon
![]() tel que
l'une quelconque des quantités
tel que
l'une quelconque des quantités ![]() soit inférieure ou
égale à la plus petite de
soit inférieure ou
égale à la plus petite de ![]() et
et ![]() .
.
Il s'en suit le corollaire :
Le canon le plus simple est unique, ou encore il existe un unique
système de quantité ![]() ,
,
![]() , ...,
, ...,
![]() qui donnent un canon le plus simple.
qui donnent un canon le plus simple.
Soient les quantités
![]() ,
,
![]() , ...,
, ...,
![]() respectivement plus grandes que
respectivement plus grandes que
![]() ,
,
![]() , ...,
, ..., ![]() et
et ![]() ,
,
![]() ,
...,
,
..., ![]() respectivement inférieures ou égales
à
respectivement inférieures ou égales
à ![]() ,
,
![]() , ...,
, ..., ![]() . Nous
appelons respectivement
. Nous
appelons respectivement ![]() et
et ![]() les quantités
qui constituent le premier et le second canon, avec
les quantités
qui constituent le premier et le second canon, avec
Comme les quantités
![]() ,
,
![]() , ...,
, ...,
![]() sont respectivement plus grandes que
sont respectivement plus grandes que
![]() ,
,
![]() , ...,
, ..., ![]() quantités elles-mêmes toutes
supposées positives ou nulles, les quantités
quantités elles-mêmes toutes
supposées positives ou nulles, les quantités
![]() ,
,
![]() , ...,
, ..., ![]() sont toutes positives. J'observe
alors qu'il ne peut se faire que dans les séries
sont toutes positives. J'observe
alors qu'il ne peut se faire que dans les séries ![]() ,
,
![]() ,...,
,..., ![]() du canon
du canon ![]() ,
,
![]() , ...,
, ...,
![]() on trouve un maximum égal à un terme placé dans la
même verticale, mais appartenant à l'une des séries restantes.
Soit en effet ce maximum dans la série
on trouve un maximum égal à un terme placé dans la
même verticale, mais appartenant à l'une des séries restantes.
Soit en effet ce maximum dans la série ![]() et le terme qui lui
est égal dans la série
et le terme qui lui
est égal dans la série ![]() , de sorte que
, de sorte que
Il découle du théorème ![]()
Théorème V. Il n'y a pas de canon pour lequel l'une des
quantités
![]() prenne
une valeur plus petite que pour le canon le plus simple.
prenne
une valeur plus petite que pour le canon le plus simple.
Supposons donné un tel canon, par la méthode précédente on
pourrait en obtenir un autre pour lequel l'une au moins des
quantités
![]() prendrait
une valeur plus petite que pour le canon le plus simple, les autres
n'étant pas plus grandes, ce qui est contraire à la définition
d'un canon le plus simple. Comme la valeur la plus petite que peuvent
prendre les quantités
prendrait
une valeur plus petite que pour le canon le plus simple, les autres
n'étant pas plus grandes, ce qui est contraire à la définition
d'un canon le plus simple. Comme la valeur la plus petite que peuvent
prendre les quantités
![]() est
est ![]() , il découle de
la proposition
, il découle de
la proposition ![]() le corollaire
le corollaire
Théorème VI. Une série qui est inchangée dans un canon quelconque l'est aussi dans le canon le plus simple.
Pour savoir si un canon quelconque est ou non le plus simple, on peut ajouter cette proposition
Théorème VII. Un canon étant donné, et ayant choisi un système de maxima
transversaux, on note d'abord ![]() les séries inchangées, puis
ensuite
les séries inchangées, puis
ensuite ![]() les séries dont les maxima sont égaux à un terme
d'une série de
les séries dont les maxima sont égaux à un terme
d'une série de ![]() situé dans la même verticale, puis
situé dans la même verticale, puis ![]() les
séries dont les maxima sont égaux à un terme d'une série
de
les
séries dont les maxima sont égaux à un terme d'une série
de ![]() situé dans la même verticale, et ainsi de suite. Si,
poursuivant ce processus, on épuise toutes les séries du canon,
le canon sera le plus simple.
situé dans la même verticale, et ainsi de suite. Si,
poursuivant ce processus, on épuise toutes les séries du canon,
le canon sera le plus simple.
Les quantités
![]() se rapportent au canon proposé et les
quantités
se rapportent au canon proposé et les
quantités
![]() ,
,
![]() , ...,
, ..., ![]() à un autre canon. Nous
supposons choisi le même système de maxima transversaux que dans
le théorème considéré, auquel répond un système de maxima
transversaux dans l'autre canon.
à un autre canon. Nous
supposons choisi le même système de maxima transversaux que dans
le théorème considéré, auquel répond un système de maxima
transversaux dans l'autre canon.
Si
![]() , le maximum de la
série
, le maximum de la
série ![]() dans l'autre canon possédera une valeur plus petite
que dans le canon proposé. Si la série
dans l'autre canon possédera une valeur plus petite
que dans le canon proposé. Si la série ![]() appartient à
l'ensemble
appartient à
l'ensemble ![]() , de sorte que, dans le canon proposé, le maximum de la
série
, de sorte que, dans le canon proposé, le maximum de la
série ![]() soit égal à un terme de la série
soit égal à un terme de la série ![]() appartenant à l'ensemble
appartenant à l'ensemble ![]() , on doit alors
avoir
, on doit alors
avoir
![]() . Appelant en effet
. Appelant en effet ![]() les termes du canon proposé et
les termes du canon proposé et ![]() ceux de l'autre, on
aura
ceux de l'autre, on
aura
Ensuite, dans le canon
proposé, le maximum de la série ![]() est égal à un terme de
la série
est égal à un terme de
la série ![]() appartenant à l'ensemble
appartenant à l'ensemble ![]() et l'on montre de
la même manière que l'on doit
avoir
et l'on montre de
la même manière que l'on doit
avoir
![]() , ce qui est absurde puisque,
selon la supposition faite,
, ce qui est absurde puisque,
selon la supposition faite,
![]() et
et
![]() sont positives ou nulles.
La réduction à l'absurde procède de la même manière, à
quelqu'ensemble
sont positives ou nulles.
La réduction à l'absurde procède de la même manière, à
quelqu'ensemble
![]() qu'appartienne la
série
qu'appartienne la
série ![]() à laquelle correspond dans l'autre canon la
quantité
à laquelle correspond dans l'autre canon la
quantité
![]() inférieure à celle du canon
proposé
inférieure à celle du canon
proposé ![]() . Donc, si le canon est tel qu'on le suppose
dans
. Donc, si le canon est tel qu'on le suppose
dans ![]() , les valeurs
, les valeurs ![]() ne peuvent prendre pour aucun autre
des valeurs inférieures; c'est-à-dire que le canon proposé
est le plus simple.
ne peuvent prendre pour aucun autre
des valeurs inférieures; c'est-à-dire que le canon proposé
est le plus simple.
Ce qui précède contient aussi la
solution du problème étant donné un canon quelconque, en
trouver un le plus simple. On peut supposer que dans le canon
donné, l'une au moins des séries est inchangée ; s'il ne s'en
trouve pas, on en obtiendra une en diminuant tous les ![]() de la même
quantité. Comme dans le théorème
de la même
quantité. Comme dans le théorème ![]() nous appelons
nous appelons ![]() l'ensemble des séries inchangées, et construisons les
ensembles
l'ensemble des séries inchangées, et construisons les
ensembles ![]() qui y sont définis. Si par ce procédé on
épuise toutes les séries, le canon, selon
qui y sont définis. Si par ce procédé on
épuise toutes les séries, le canon, selon ![]() , est déjà
le plus simple. Supposons qu'il reste des séries dépourvues
de tels maxima, auxquels soient égaux des termes de la
même verticale appartenant aux ensembles formés. Alors les
termes des séries restantes (ou les quantités
, est déjà
le plus simple. Supposons qu'il reste des séries dépourvues
de tels maxima, auxquels soient égaux des termes de la
même verticale appartenant aux ensembles formés. Alors les
termes des séries restantes (ou les quantités ![]() qui se
rapportent à ces séries) peuvent toutes être diminuées
d'un même quantité jusqu'à ce que l'une de leurs quantités
qui se
rapportent à ces séries) peuvent toutes être diminuées
d'un même quantité jusqu'à ce que l'une de leurs quantités ![]() ne s'annule ou que l'un de leurs maxima ne décroisse
jusqu'à égaler un terme situé dans la même verticale et
appartenant aux ensembles formés. Ceci fait, on obtient un
nouveau canon, dans lequel le nombre des séries appartenant aux
ensembles fomés selon la règle indiquée est
augmenté. Si toutes les séries entrent dans ces ensembles, le
canon obtenu sera le plus simple. Sinon, de nouveaux canons sont à
construire en répétant la même méthode, toujours moins
de séries restant en dehors des ensembles qui peuvent être
formés, jusqu'à ce que l'on parvienne à un canon dans
lequel ces ensembles épuiseront toutes les séries et qui est
le canon le plus simple cherché.
ne s'annule ou que l'un de leurs maxima ne décroisse
jusqu'à égaler un terme situé dans la même verticale et
appartenant aux ensembles formés. Ceci fait, on obtient un
nouveau canon, dans lequel le nombre des séries appartenant aux
ensembles fomés selon la règle indiquée est
augmenté. Si toutes les séries entrent dans ces ensembles, le
canon obtenu sera le plus simple. Sinon, de nouveaux canons sont à
construire en répétant la même méthode, toujours moins
de séries restant en dehors des ensembles qui peuvent être
formés, jusqu'à ce que l'on parvienne à un canon dans
lequel ces ensembles épuiseront toutes les séries et qui est
le canon le plus simple cherché.



À partir du tableau proposé, en ajoutant aux termes des différentes
séries les nombres respectifs ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , on
obtient un nouveau tableau, dans lequel des termes maximaux parmi tous
ceux de leur verticale sont dans des séries horizontales différentes,
ce qui est la propriété caractéristique d'un canon.
, on
obtient un nouveau tableau, dans lequel des termes maximaux parmi tous
ceux de leur verticale sont dans des séries horizontales différentes,
ce qui est la propriété caractéristique d'un canon.
On se propose de rechercher un canon le plus simple. La série VII
constitue dans le canon donné l'ensemble ![]() . Je soustrais l'unité des termes
des autres séries, ce qui produit le canon dérivé I.
. Je soustrais l'unité des termes
des autres séries, ce qui produit le canon dérivé I.
Dans le canon dérivé I, les séries IV et VII constituent l'ensemble
![]() , la série I l'ensemble
, la série I l'ensemble ![]() . Je soustrais
. Je soustrais ![]() des autres termes, ce
qui produit le canon dérivé II.
des autres termes, ce
qui produit le canon dérivé II.
Dans le canon dérivé II, les séries III, IV, VII
constituent l'ensemble ![]() , les séries I et VI l'ensemble
, les séries I et VI l'ensemble ![]() ; je
soustrais l'unité des deuxième et cinquième séries, ce
qui produit le dernier canon ou canon le plus simple, qui correspond
aux valeurs de
; je
soustrais l'unité des deuxième et cinquième séries, ce
qui produit le dernier canon ou canon le plus simple, qui correspond
aux valeurs de ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . En ajoutant
celles-ci aux termes des diverses séries du tableau
proposé, on obtient le canon le plus simple. Les séries III,
IV, VII constituent l'ensemble
. En ajoutant
celles-ci aux termes des diverses séries du tableau
proposé, on obtient le canon le plus simple. Les séries III,
IV, VII constituent l'ensemble ![]() , les séries I, II, V, VI
l'ensemble
, les séries I, II, V, VI
l'ensemble ![]() ; nous voyons que ces ensembles épuisent toutes les
séries, ce qui est la propriété caractéristique du
canon le plus simple.
; nous voyons que ces ensembles épuisent toutes les
séries, ce qui est la propriété caractéristique du
canon le plus simple.
Si on ne donne pas de canon mais seulement les termes du tableau proposé qui constituent une somme transversale maximale, on parvient au canon le plus simple en ajoutant à chaque série la quantité minimale pour que le terme de cette série appartenant à la somme transversale maximale soit rendu égal au maximum de sa verticale. Ayant appliqué ce procédé à chaque série et l'ayant répété si nécessaire, on doit parvenir à un canon qui sera le plus simple, puisqu'on n'ajoute pas d'incrément aux séries qui soit plus grand que ce qui est nécessaire pour que les termes donnés soient rendus maximaux dans leurs verticales respectives.
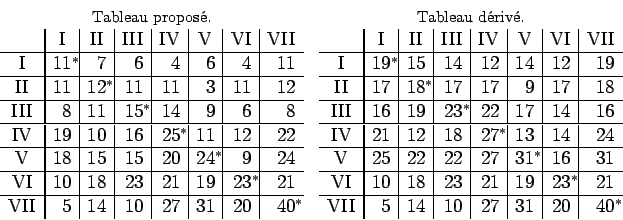

Les termes notés d'un astérisques forment une somme transversale maximale, il apparaît que j'ai tiré le tableau proposé du canon précédent en changeant les séries horizontales en verticales et les verticales en horizontales; ce faisant, les mêmes termes constituent une somme transversale maximale, mais le tableau cesse d'être un canon.
Au séries
Aux séries
Comme, étant donné un canon, on connaît aussi une somme transversale maximale du tableau proposé, on peut ramener au problème résolu par ce qui précède cet autre problème, étant donné un canon quelconque, rechercher le plus simple. Celui-ci aura donc deux solutions, l'une par soustractions successives, comme plus haut, l'autre procédant par additions successives, à savoir que si nous tirons du canon donné une somme transversale maximale du tableau proposé, nous appliquons, celle-ci connue, la méthode précédente.
Dans le tableau préparatoire, je cherche le nombre maximal de maxima transversaux, quand il y a plusieurs choix possibles, il suffit d'en considérer au moins un. Ce choix fait, je résouds le problème proposé en augmentant successivement le nombre de maxima transversaux jusqu'à ce qu'on obtienne un tableau doté d'un système complet de maxima transversaux qui sera le canon recherché. Il suffit donc de démontrer qu'on peut accroître d'une unité le nombre de maxima transversaux par une augmentation idoine des séries.
| A | C |
| B | D |
Je divise le tableau préparatoire en quatre parties comme dans la
figure ci-contre. Nous supposons que les maxima transversaux choisis
sont tous dans la partie ![]() , de sorte que les séries où sont ces
maxima occupent les parties
, de sorte que les séries où sont ces
maxima occupent les parties ![]() et
et ![]() ; les verticales auxquelles ils
appartiennent occupent les parties
; les verticales auxquelles ils
appartiennent occupent les parties ![]() et
et ![]() . J'appelle supérieures
les séries occupant les parties
. J'appelle supérieures
les séries occupant les parties ![]() et
et ![]() et inférieures celles
occupant les parties
et inférieures celles
occupant les parties ![]() et
et ![]() . J'appelle ensuite gauches les
verticales occupant les parties
. J'appelle ensuite gauches les
verticales occupant les parties ![]() et
et ![]() et droites les verticales
occupant les parties
et droites les verticales
occupant les parties ![]() et
et ![]() . Dès lors, dans la partie
. Dès lors, dans la partie ![]() ne se
trouve aucun maximum. Sans quoi, le nombre de maxima transversaux
serait augmenté, contredisant l'hypothèse que l'on en a choisi un
nombre maximal. Les verticales droites ont donc leurs maxima en
ne se
trouve aucun maximum. Sans quoi, le nombre de maxima transversaux
serait augmenté, contredisant l'hypothèse que l'on en a choisi un
nombre maximal. Les verticales droites ont donc leurs maxima en ![]() ;
les termes maximaux dans leurs verticales des séries inférieures
seront en
;
les termes maximaux dans leurs verticales des séries inférieures
seront en ![]() , et chacun d'eux sera égal à un maximum de la même
verticale placé en
, et chacun d'eux sera égal à un maximum de la même
verticale placé en ![]() , puisque dans l'espace
, puisque dans l'espace ![]() se trouvent les
maxima de toutes les verticales de gauche de même que de toutes les
séries supérieures.
se trouvent les
maxima de toutes les verticales de gauche de même que de toutes les
séries supérieures.
Ceci posé, je partage toutes les séries en trois classes qui sont définies comme suit.
Je choisis celles des séries supérieures qui, outre des maxima
en ![]() , en possèdent même d'autres placés en
, en possèdent même d'autres placés en ![]() , de telle sorte
qu'une au moins de ces séries existe. Supposons que l'un des maxima
de ces séries placé en
, de telle sorte
qu'une au moins de ces séries existe. Supposons que l'un des maxima
de ces séries placé en ![]() soit égal à un autre terme de la
même verticale ; on recherche un maximum placé dans la même
série que ce terme et s'il est égal à un autre terme dans la
même verticale, nous cherchons de nouveau un maximum placé dans la
même série que ce terme, et ainsi de suite. Toutes les séries
auxquelles on peut parvenir par ce moyen, depuis les séries de
départ, constituent la première classe.
soit égal à un autre terme de la
même verticale ; on recherche un maximum placé dans la même
série que ce terme et s'il est égal à un autre terme dans la
même verticale, nous cherchons de nouveau un maximum placé dans la
même série que ce terme, et ainsi de suite. Toutes les séries
auxquelles on peut parvenir par ce moyen, depuis les séries de
départ, constituent la première classe.
Je dis que, parmi les séries de la première classe, ne se trouvent
pas de série inférieure, ni de série supérieure à partir
de laquelle on puisse parvenir à une série inférieure par le
moyen indiqué. En effet, étant parti d'une série qui, outre un
maximum en ![]() en possède un ailleurs en
en possède un ailleurs en ![]() , on considère un
système de maxima placés en
, on considère un
système de maxima placés en ![]() auxquels on est parvenu par la
méthode indiquée, dont le dernier, si cela se peut, est égal à
un terme de la même verticale placé en
auxquels on est parvenu par la
méthode indiquée, dont le dernier, si cela se peut, est égal à
un terme de la même verticale placé en ![]() . Tous ces maxima
placés en
. Tous ces maxima
placés en ![]() sont, par hypothèse, transversaux et on obtiendra à
leur place un autre système de maxima transversaux si l'on substitue
à chacun d'entre eux un terme égal placé sur la même
verticale. De la sorte, on substitue au dernier maximum le terme
placé en
sont, par hypothèse, transversaux et on obtiendra à
leur place un autre système de maxima transversaux si l'on substitue
à chacun d'entre eux un terme égal placé sur la même
verticale. De la sorte, on substitue au dernier maximum le terme
placé en ![]() , sans plus utiliser la première série, dont nous
sommes parti. En adjoignant le maximum de cette série placé en
, sans plus utiliser la première série, dont nous
sommes parti. En adjoignant le maximum de cette série placé en ![]() pour former un nouveau système de maxima, le nombre des maxima
transversaux augmente d'une unité, ce qui contredit la supposition
que ce nombre était maximal.
pour former un nouveau système de maxima, le nombre des maxima
transversaux augmente d'une unité, ce qui contredit la supposition
que ce nombre était maximal.
Les séries supérieures qui n'appartiennent pas à la première classe et à partir desquelles on ne peut parvenir par le moyen indiqué à une série inférieure appartiennent à la seconde classe. Il peut se faire que cette classe soit vide.
Appartiennent enfin à la troisième classe toutes les séries inférieures et les séries supérieures à partir desquelles la méthode indiquée donne accès aux séries inférieures. Donc, si un terme d'une série inférieure est égal à un maximum d'une série supérieure sur la même verticale -- ce qui est toujours le cas -- cette série supérieure appartiendra à la troisième classe. La troisième classe, sauf si le tableau est déjà un canon, contient au moins deux séries, l'une inférieure, l'autre supérieure.
J'exprimerai de nouveau ce que j'ai démontré au sujet de la
première classe en disant que, parmi les séries supérieures de
la troisième classe, il ne s'en trouve aucune qui possède un
maximum placé en ![]() . J'utiliserai par la suite cette forme de la
proposition.
. J'utiliserai par la suite cette forme de la
proposition.
Les observations faites à cette occasion produisent en même temps une méthode pour faire apparaître le nombre maximal de maxima transversaux dans le tableau préparatoire. En effet, ayant posé un tel système de maxima transversaux, s'offrant de prime abord, cette classification des séries indique si leur nombre peut être augmenté.
La classification ainsi décrite étant faite, toute la troisième classe est augmentée d'une quantité identique et la plus petite qui fasse qu'un terme des séries de cette classe atteigne un terme maximal placé sur la même verticale appartenant à une série de la première ou de la seconde classe.
Ainsi, si le maximum appartient à la première classe, le nombre de
maxima transversaux peut être augmenté. Soit en effet une série
supérieure qui possède, outre un maximum en ![]() , un autre en
, un autre en ![]() et
d'où l'on puisse aller par le moyen indiqué à une série
inférieure. Cette série est à compter au nombre des séries
supérieures tandis qu'on doit augmenter celui des verticales de
gauche par la verticale de droite dans laquelle se trouve ce maximum
placé en
et
d'où l'on puisse aller par le moyen indiqué à une série
inférieure. Cette série est à compter au nombre des séries
supérieures tandis qu'on doit augmenter celui des verticales de
gauche par la verticale de droite dans laquelle se trouve ce maximum
placé en ![]() . Si le terme d'une série de la troisième classe,
égal à un maximum d'une série de la première, se trouve
en
. Si le terme d'une série de la troisième classe,
égal à un maximum d'une série de la première, se trouve
en ![]() , les maxima transversaux restent inchangés, il suffit
d'ajouter ce terme. Si encore ce terme se trouve en
, les maxima transversaux restent inchangés, il suffit
d'ajouter ce terme. Si encore ce terme se trouve en ![]() , il faut
changer tous les maxima formant cette chaîne par laquelle on
descend jusqu'à la série inférieure depuis la série contenant
le maximum en
, il faut
changer tous les maxima formant cette chaîne par laquelle on
descend jusqu'à la série inférieure depuis la série contenant
le maximum en ![]() . À savoir que chacun de ces maxima transversaux est
à remplacer par le terme de la même verticale qui lui est égal,
le dernier donc par ce terme en
. À savoir que chacun de ces maxima transversaux est
à remplacer par le terme de la même verticale qui lui est égal,
le dernier donc par ce terme en ![]() , de nouveaux maxima transversaux
apparaissant ainsi en ajoutant au début le terme de la première
série13, comme
je l'ai fait remarquer au sujet de la première classe.
, de nouveaux maxima transversaux
apparaissant ainsi en ajoutant au début le terme de la première
série13, comme
je l'ai fait remarquer au sujet de la première classe.
Si le maximum auquel est égal un terme de la troisième classe se trouve dans une série de la seconde, rien ne change, sinon que ces séries passent dans la troisième classe en même temps que toutes les séries restantes de la seconde classe à partir desquelles, par la chaîne indiquée, on atteint cette série. Répétant cette opération de nouveau, ou on augmente le nombre de maxima transversaux, ou on diminue celui des séries de la seconde classe, à moins qu'avant que le nombre de maxima transversaux ne soit augmenté on ne parvienne à un tableau privé des séries de la seconde classe, parce que toutes seront passées dans la troisième. Mais alors, par l'opération indiqué, on obtiendra assurément une augmentation des maxima transversaux. Y étant parvenu, il faut, dans les différents cas qui peuvent se produire et qu'il serait long d'énumérer, effectuer une nouvelle répartition des maxima transversaux en les trois classes indiquées et, ceci fait, répéter l'opération jusqu'à ce qu'on parvienne à un canon dans lequel les séries inférieures seront toutes devenues supérieures et les verticales de droite devenues de gauche.
Et par la méthode précédemment décrite, on obtient non seulement un canon, mais un canon le plus simple. Pour le prouver, je démontrerai que les quantités dont sont augmentées les séries sont minimales, parce qu'elles sont exigées pour produire tout canon. Tout d'abord, en ce qui concerne l'opération préparatoire, j'observe que chaque terme du canon est supérieur ou égal au terme correspondant du tableau donné, comme le canon est obtenu en ajoutant à chaque série du tableau uniquement des quantités positives ou nulles. Donc, le maximum dans chaque verticale du canon est supérieur ou égal au maximum dans la même verticale du tableau donné. Or, dans les canons, se trouve dans chaque série un maximum, donc un terme qui est supérieur ou égal au maximum du tableau donné placé dans la même verticale ; nous devons donc augmenter chaque série du tableau donné privé de maximum d'une quantité telle que l'un de ses termes devienne supérieur ou égal au maximum de la même verticale. Si alors nous considérons les quantités dont diffèrent chaque terme d'une série des maxima de la même verticale, la quantité dont la série doit être augmentée ne doit pas être inférieure au minimum de ces quantités. Ainsi donc, en augmentant chaque série privée de maximum de la quantité minimale qui rendra l'un de ses termes égal au maximum de la même verticale, ces séries ne sont certainement pas augmentée de quantités plus grandes que ce qui est exigé pour former le canon.
La préparation faite, si elle fournit déjà par elle-même un canon, celui-ci est certainement le plus simple ; nous avons vu en effet que des quantités positives, minimales pour fournir un canon, sont ajoutées aux séries du tableau proposé. Mais si un canon n'est pas encore apparu, il a fallu procéder à la distribution des séries en trois classes. Je vais maintenant démontrer que pour produire un canon, il ne peut se faire que l'une des séries de la troisième classe demeure inchangée.
Dans la démonstration, j'appellerai ![]() le tableau
préparatoire,
le tableau
préparatoire, ![]() le canon obtenu. Je suppose toujours que la
classification des séries a nécessité de considérer en
le canon obtenu. Je suppose toujours que la
classification des séries a nécessité de considérer en ![]() un
certain système de maxima transversaux dans l'espace
un
certain système de maxima transversaux dans l'espace ![]() , de sorte
que s'il se trouve plusieurs systèmes de la sorte en
, de sorte
que s'il se trouve plusieurs systèmes de la sorte en ![]() , l'un
quelconque d'entre eux doive être choisi. De même dans
, l'un
quelconque d'entre eux doive être choisi. De même dans ![]() , je
suppose, si plusieurs systèmes de maxima transversaux se
présentent, que l'on en a choisi un.
, je
suppose, si plusieurs systèmes de maxima transversaux se
présentent, que l'on en a choisi un.
Nous considérons en ![]() , s'il s'en présente, l'ensemble de toutes
les séries supérieures de la troisième classe inchangées,
c'est-à-dire celles auxquelles nulle quantité n'est ajoutée pour
former le canon
, s'il s'en présente, l'ensemble de toutes
les séries supérieures de la troisième classe inchangées,
c'est-à-dire celles auxquelles nulle quantité n'est ajoutée pour
former le canon ![]() , ou encore qui sont en
, ou encore qui sont en ![]() et
et ![]() identiques. Nous
appelons
identiques. Nous
appelons ![]() l'ensemble de ces séries et nous considérons des
maxima transversaux de celles-ci choisis dans
l'ensemble de ces séries et nous considérons des
maxima transversaux de celles-ci choisis dans ![]() et
et ![]() . Je dis que
les systèmes de ces maxima dans
. Je dis que
les systèmes de ces maxima dans ![]() et
et ![]() seront dans les mêmes
verticales. Soit en effet
seront dans les mêmes
verticales. Soit en effet ![]() l'un de ces maxima dans
l'un de ces maxima dans ![]() placé dans
une série inchangée, il lui correspond dans
placé dans
une série inchangée, il lui correspond dans ![]() un terme égal de
la même série et lui-même maximal dans sa verticale. Car, comme
on passe de
un terme égal de
la même série et lui-même maximal dans sa verticale. Car, comme
on passe de ![]() à
à ![]() par additions positives, les termes de cette
verticale en
par additions positives, les termes de cette
verticale en ![]() sont inférieurs ou égaux aux termes correspondants
de
sont inférieurs ou égaux aux termes correspondants
de ![]() ; donc si leur maximum en
; donc si leur maximum en ![]() est égal à un terme de
est égal à un terme de ![]() dans la même verticale, celui-ci doit être à plus forte raison maximal
parmi les termes de la même verticale dans
dans la même verticale, celui-ci doit être à plus forte raison maximal
parmi les termes de la même verticale dans ![]() . Le terme
. Le terme ![]() doit
appartenir à l'espace
doit
appartenir à l'espace ![]() car, selon les propriétés des
classes, une série supérieure de la troisième classe n'a pas de
terme maximal dans sa verticale placé en
car, selon les propriétés des
classes, une série supérieure de la troisième classe n'a pas de
terme maximal dans sa verticale placé en ![]() . Nous appelons
. Nous appelons ![]() l'ensemble des verticales dans lesquelles sont les maxima des
séries
de
l'ensemble des verticales dans lesquelles sont les maxima des
séries
de ![]() dans
dans ![]() et nous supposons que la verticale dans laquelle
est
et nous supposons que la verticale dans laquelle
est ![]() n'appartient pas aux verticales de
n'appartient pas aux verticales de ![]() . Il existera en
. Il existera en ![]() dans cette verticale un maximum
dans cette verticale un maximum ![]() appartenant aux maxima
transversaux choisis dans l'espace
appartenant aux maxima
transversaux choisis dans l'espace ![]() et c'est pourquoi ce maximum
et c'est pourquoi ce maximum ![]() sera
placé dans une série qui ne fait pas partie de celle de
sera
placé dans une série qui ne fait pas partie de celle de ![]() . Les
maxima transversaux choisis dans les séries
. Les
maxima transversaux choisis dans les séries ![]() sont eux-mêmes
dans les verticales de
sont eux-mêmes
dans les verticales de ![]() , alors que
, alors que ![]() est supposé être dans
une verticale n'appartenant pas à
est supposé être dans
une verticale n'appartenant pas à ![]() . Cette nouvelle
série14 doit être une série supérieure appartenant à la
troisième classe ; le maximum
. Cette nouvelle
série14 doit être une série supérieure appartenant à la
troisième classe ; le maximum ![]() appartient en effet à
l'espace
appartient en effet à
l'espace ![]() et il résulte de la définition des classes donnée
que si, dans la même verticale, se trouvent des termes maximaux tous
égaux entre eux, les séries dans lesquelles ils ont placés
appartiennent à la même classe. Alors, si pour former le
canon
et il résulte de la définition des classes donnée
que si, dans la même verticale, se trouvent des termes maximaux tous
égaux entre eux, les séries dans lesquelles ils ont placés
appartiennent à la même classe. Alors, si pour former le
canon ![]() , on ajoutait à cette série une quantité non nulle, le
terme de
, on ajoutait à cette série une quantité non nulle, le
terme de ![]() correspondant à
correspondant à ![]() se trouverait plus grand que
se trouverait plus grand que ![]() ,
et donc aussi plus grand que le terme
,
et donc aussi plus grand que le terme ![]() placé dans la même
verticale, ce qui ne peut pas se produire puisque
placé dans la même
verticale, ce qui ne peut pas se produire puisque ![]() est maximal dans
sa verticale. Cette série doit donc elle-même être inchangée,
ce qui est aussi absurde car on a supposé que les séries de
est maximal dans
sa verticale. Cette série doit donc elle-même être inchangée,
ce qui est aussi absurde car on a supposé que les séries de ![]() sont l'ensemble de toutes les séries inchangées de la troisième
classe. Donc
sont l'ensemble de toutes les séries inchangées de la troisième
classe. Donc ![]() lui-même se trouve nécessairement dans une
verticale de
lui-même se trouve nécessairement dans une
verticale de ![]() ; comme ceci vaut pour chacun des maxima, il s'ensuit
que le système des maxima transversaux des séries de
; comme ceci vaut pour chacun des maxima, il s'ensuit
que le système des maxima transversaux des séries de ![]() choisis
dans
choisis
dans ![]() sont dans les mêmes verticales que le système des maxima
transversaux de ces mêmes séries choisis dans
sont dans les mêmes verticales que le système des maxima
transversaux de ces mêmes séries choisis dans ![]() ; C.Q.F.D.
; C.Q.F.D.
Si l'on prend dans ![]() des termes correspondants et égaux aux maxima
des séries de
des termes correspondants et égaux aux maxima
des séries de ![]() dans
dans ![]() , ceux-ci formeront dans
, ceux-ci formeront dans ![]() un autre
système de maxima transversaux qui sont dans les mêmes séries
horizontales et verticales. Ce qui ne peut se faire, à moins
que les termes des deux systèmes placés dans les mêmes
verticales ne soient égaux entre eux. D'où provient ce
corollaire : si l'on prend dans
un autre
système de maxima transversaux qui sont dans les mêmes séries
horizontales et verticales. Ce qui ne peut se faire, à moins
que les termes des deux systèmes placés dans les mêmes
verticales ne soient égaux entre eux. D'où provient ce
corollaire : si l'on prend dans ![]() , dans une série inchangée de la
troisième classe, un maximum, on aura dans
, dans une série inchangée de la
troisième classe, un maximum, on aura dans ![]() un maximum égal,
dans la même verticale, dans une série supérieure de la même
classe. Je suppose toujours que les maxima dans
un maximum égal,
dans la même verticale, dans une série supérieure de la même
classe. Je suppose toujours que les maxima dans ![]() ou dans
ou dans ![]() sont
pris dans les systèmes choisis de maxima transversaux.
sont
pris dans les systèmes choisis de maxima transversaux.
Pour le reste, la proposition précédente se démontre de la
même manière si ![]() désigne l'ensemble des séries
inchangées de la seconde classe ; c'est en revanche seulement pour
celles-ci que la proposition possède force et signification. En
effet, les séries inchangées de la troisième classe n'existent
absolument pas.
désigne l'ensemble des séries
inchangées de la seconde classe ; c'est en revanche seulement pour
celles-ci que la proposition possède force et signification. En
effet, les séries inchangées de la troisième classe n'existent
absolument pas.
Il apparaît d'abord qu'on n'a pas de séries inférieures
inchangées. Si en effet, il y a une série inférieure
inchangée, soit ![]() son maximum dans
son maximum dans ![]() , tiré du système de
maxima transversaux choisis ; ce même terme sera en
, tiré du système de
maxima transversaux choisis ; ce même terme sera en ![]() maximal
parmi tous ceux de la même verticale et pour cela est égal à un
maximum d'une série de la troisième classe placé dans la même
verticale et appartenant aux maxima transversaux15. Mais, selon le corollaire
précédant, il doit se
trouver dans
maximal
parmi tous ceux de la même verticale et pour cela est égal à un
maximum d'une série de la troisième classe placé dans la même
verticale et appartenant aux maxima transversaux15. Mais, selon le corollaire
précédant, il doit se
trouver dans ![]() dans la même verticale un maximum d'une série
supérieure appartenant aux maxima transversaux, d'où l'on aura
dans
dans la même verticale un maximum d'une série
supérieure appartenant aux maxima transversaux, d'où l'on aura
dans ![]() , dans la même verticale, deux maxima transversaux, l'un dans
une série supérieure, l'autre
, dans la même verticale, deux maxima transversaux, l'un dans
une série supérieure, l'autre ![]() dans une inférieure, ce qui
est contraire à la notion de maxima transversaux.
dans une inférieure, ce qui
est contraire à la notion de maxima transversaux.
Je vais maintenant démontrer que, s'il y a une série la troisième classe supérieure inchangée, il y en a une inférieure inchangée ; comme c'est impossible, il sera prouvé qu'il n'y a de série inchangée de la troisième classe, ni inférieure ni supérieure.
Supposons donnée une série supérieure
inchangée de la troisième classe que je désigne par ![]() . Selon
la définition de la troisième classe, on aura des séries
. Selon
la définition de la troisième classe, on aura des séries ![]() ,
,
![]() ,
, ![]() , ...,
, ..., ![]() telles que leurs maxima
telles que leurs maxima
![]() qui sont tirés du système de maxima
transversaux choisis, ont chacun dans la même verticale un terme
égal
qui sont tirés du système de maxima
transversaux choisis, ont chacun dans la même verticale un terme
égal ![]() dans la série suivante, le dernier
dans la série suivante, le dernier ![]() étant
égal à un terme
étant
égal à un terme ![]() de la même verticale dans une série
inférieure, de sorte que
de la même verticale dans une série
inférieure, de sorte que ![]() et
et ![]() sont tout deux dans la
même série, et que
sont tout deux dans la
même série, et que ![]() et
et ![]() sont tous deux égaux et
dans la même verticale. Alors, si une série supérieure
sont tous deux égaux et
dans la même verticale. Alors, si une série supérieure ![]() de la
troisième classe est inchangée, on aura selon le corollaire
précédent un maximum dans
de la
troisième classe est inchangée, on aura selon le corollaire
précédent un maximum dans ![]() égal à
égal à ![]() lui-même et placé
dans la même verticale ; d'où il sera impossible pour former le
canon d'augmenter la série
lui-même et placé
dans la même verticale ; d'où il sera impossible pour former le
canon d'augmenter la série ![]() , sans quoi, en effet, on
augmenterait le terme
, sans quoi, en effet, on
augmenterait le terme ![]() et le maximum
et le maximum ![]() lui-même, placé dans
la même verticale, disparaîtrait. La série
lui-même, placé dans
la même verticale, disparaîtrait. La série ![]() doit donc
elle aussi être inchangée, et l'on prouve de même que chacune
des séries
doit donc
elle aussi être inchangée, et l'on prouve de même que chacune
des séries
![]() , ainsi que la série
inférieure
, ainsi que la série
inférieure ![]() , sont inchangées, ce que nous avons vu être
impossible.
, sont inchangées, ce que nous avons vu être
impossible.
Comme, pour former le canon, aucune série de la
troisième classe ne peut rester inchangée, soit ![]() la plus petite
des quantités par lesquelles ces séries doivent être
augmentées pour que, étant toutes augmentées de
la plus petite
des quantités par lesquelles ces séries doivent être
augmentées pour que, étant toutes augmentées de ![]() , il s'en
trouve dans le nouveau tableau au moins une, qui pour former le canon
ne doive pas être augmentée davantage, mais demeure inchangée.
Soit
, il s'en
trouve dans le nouveau tableau au moins une, qui pour former le canon
ne doive pas être augmentée davantage, mais demeure inchangée.
Soit ![]() la quantité minimale dont on augmente une série
la quantité minimale dont on augmente une série ![]() de la
troisième classe pour que l'un de ses termes devienne égal au
maximum d'une série de la première ou de la seconde classe placé
dans la même verticale. Si
de la
troisième classe pour que l'un de ses termes devienne égal au
maximum d'une série de la première ou de la seconde classe placé
dans la même verticale. Si ![]() 16 et que toutes les
séries de la troisième classe
16 et que toutes les
séries de la troisième classe ![]() sont augmentées
de
sont augmentées
de
![]() , nous voyons que dans le nouveau tableau la
répartition des séries en classes n'est pas modifiée, et que
chacune appartient à la même classe que dans
, nous voyons que dans le nouveau tableau la
répartition des séries en classes n'est pas modifiée, et que
chacune appartient à la même classe que dans ![]() . Il ne pourra
donc y avoir
. Il ne pourra
donc y avoir ![]() ; sinon en effet, on aurait un tableau dans lequel
se trouveraient des séries inchangées de la troisième classe, ce
qui ne peut être. Nous voyons de là que la quantité minimale
dont les séries de la troisième classe doivent être augmentées
pour que l'un de leurs termes atteigne un maximum d'une série de la
première ou de la seconde classe placé dans la même verticale
et inférieur ou égal à la plus petite des quantités dont les
séries de la troisième classe doivent être augmentées pour
former le canon. D'où il procède que, par la règle énoncée, on
n'effectue jamais d'additions supérieures à ce qui est
nécessaire pour former un quelconque canon et à cause de cela,
le canon obtenu par notre règle sera le plus simple.
; sinon en effet, on aurait un tableau dans lequel
se trouveraient des séries inchangées de la troisième classe, ce
qui ne peut être. Nous voyons de là que la quantité minimale
dont les séries de la troisième classe doivent être augmentées
pour que l'un de leurs termes atteigne un maximum d'une série de la
première ou de la seconde classe placé dans la même verticale
et inférieur ou égal à la plus petite des quantités dont les
séries de la troisième classe doivent être augmentées pour
former le canon. D'où il procède que, par la règle énoncée, on
n'effectue jamais d'additions supérieures à ce qui est
nécessaire pour former un quelconque canon et à cause de cela,
le canon obtenu par notre règle sera le plus simple.
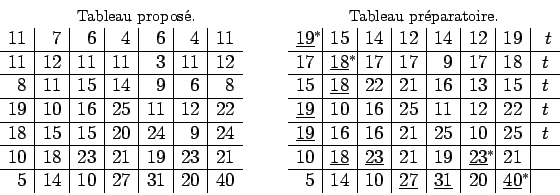
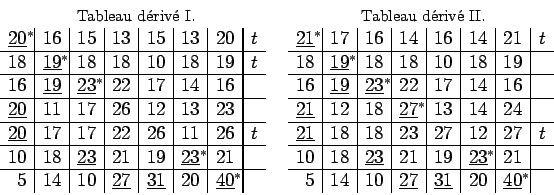
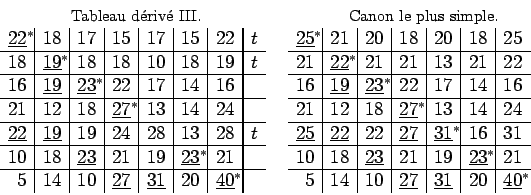
Dans le tableau proposé, les trois premières series et la
cinquième n'ont pas de termes maximaux. Il faut ajouter
respectivement à ces séries les nombres minimaux ![]() ,
, ![]() ,
,
![]() ,
, ![]() , par lesquels on peut faire que l'un de leurs termes devienne
maximal. Dans le tableau ainsi préparé, j'ai souligné tous
les termes maximaux de chaque verticale et mis une étoile en
exposant aux maxima transversaux choisis (noté par un
astérisque). Enfin, j'ai noté d'un
, par lesquels on peut faire que l'un de leurs termes devienne
maximal. Dans le tableau ainsi préparé, j'ai souligné tous
les termes maximaux de chaque verticale et mis une étoile en
exposant aux maxima transversaux choisis (noté par un
astérisque). Enfin, j'ai noté d'un ![]() les séries de la
troisième classe que l'on trouve ainsi. D'abord, y appartiennent
toutes les séries
les séries de la
troisième classe que l'on trouve ainsi. D'abord, y appartiennent
toutes les séries ![]() qui n'ont pas de terme étoilé,
que j'ai appelées ci-dessus inférieures ; ensuite les
séries
qui n'ont pas de terme étoilé,
que j'ai appelées ci-dessus inférieures ; ensuite les
séries ![]() qui ont un terme étoilé dans une verticale
où a déjà été souligné un terme d'une
série
qui ont un terme étoilé dans une verticale
où a déjà été souligné un terme d'une
série ![]() ; si, outre les termes étoilés, les
séries
; si, outre les termes étoilés, les
séries ![]() ont d'autres termes soulignés, on cherche dans
les mêmes verticales de nouveaux termes étoilés, qui
appartiennent aux séries
ont d'autres termes soulignés, on cherche dans
les mêmes verticales de nouveaux termes étoilés, qui
appartiennent aux séries ![]() , et ainsi de suite: toutes les
séries
, et ainsi de suite: toutes les
séries ![]() ,
, ![]() ,
, ![]() etc. aisément trouvées
forment la troisième classe. Il apparaît aussi que pour
appliquer la règle jusqu'au bout, il faut seulement demander de
connaître les séries de la troisième classe et que la
répartition en première et seconde classe est inutile. La
règle en effet n'exige rien d'autre que d'augmenter ensemble
toutes les séries de la troisième classe d'une quantité
minimale qui fasse que l'un de leurs termes devienne égal à
l'un des termes maximaux étoilés des autres séries,
situé dans la même verticale. Tout le travail consiste en
effet en cette augmentation des séries, le choix de maxima
transversaux et la détermination des séries de la
troisième classe, après laquelle une augmentation est de
nouveau effectuée. Ce qui doit être continué jusqu'à
ce que l'on ne trouve plus de séries de la troisième classe,
auquel cas on est parvenu au canon le plus simple.
etc. aisément trouvées
forment la troisième classe. Il apparaît aussi que pour
appliquer la règle jusqu'au bout, il faut seulement demander de
connaître les séries de la troisième classe et que la
répartition en première et seconde classe est inutile. La
règle en effet n'exige rien d'autre que d'augmenter ensemble
toutes les séries de la troisième classe d'une quantité
minimale qui fasse que l'un de leurs termes devienne égal à
l'un des termes maximaux étoilés des autres séries,
situé dans la même verticale. Tout le travail consiste en
effet en cette augmentation des séries, le choix de maxima
transversaux et la détermination des séries de la
troisième classe, après laquelle une augmentation est de
nouveau effectuée. Ce qui doit être continué jusqu'à
ce que l'on ne trouve plus de séries de la troisième classe,
auquel cas on est parvenu au canon le plus simple.
On peut, par divers artifices, s'épargner la tâche de réécrire tout le tableau après un changement quelconque. À savoir que pour passer d'un tableau au suivant, il n'est pas nécessaire d'avoir d'autres termes sous les yeux que ceux qui sont maximaux dans chaque verticale et ceux immédiatement inférieurs, et qu'il suffit d'écrire ceux-ci. Ensuite, il n'est pas nécessaire de respecter l'ordre des séries, il suffit de rayer les séries à augmenter et de les réécrire en dessous de celles qui n'ont pas été changées. Mais ces moyens et d'autres qui sont commodément employés pour une grande masse de nombres sont laissés au choix de chacun. cm
to to 4cm