- ... C.W. Borchardt1
- S. Cohn s'était déjà consacré à cet article de
l'ill. Jacobi, mais emporté par une mort prématurée,
il ne laissa pas de manuscrit prêt pour l'impression. [Note non
reproduite dans les uvres complètes. N.d.T.]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
p. 297-320)2
- «De investigando ordine systematis aequationum
differentialum vulgarium cujuscunque», reproduit dans C.G.J. Jacobi's gesammelte Werke, fünfter Band, herausgegeben von
K. Weierstrass, Berlin, Bruck und Verlag von Georg Reimer, 1890,
p. 193-216, traduit du latin par F. Ollivier (CNRS, LIX UMR CNRS 7161,
École polytechnique, 91128 Palaiseau CEDEX,
mél. francois.ollivier@lix.polytechnique.fr) avec l'aide
d'Alexandre Sedoglavic (LIFL, UMR CNRS 8022, Université des Sciences
et Technologies de Lille, 59655 Villeneuve d'Ascq CEDEX,
mél. sedoglav@lifl.fr). (N.d.T.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
canonique3
- Le système que l'on appelle ici canonique ou en
forme canonique est le même qui dans «Theoria novi
multiplicatoris » est dit mis en forme normale (J. de Crelles
tome
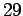 p.
p. 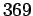 , cf. C.G.J. Jacobi gesammelte Werke,
vol. 4, p. 501) mais diffère entièrement de celui que Jacobi
qualifie de canonique dans «Nova methodus aeq. diff. partiales
primi ordinis integrandi » (J. de Crelles tome
, cf. C.G.J. Jacobi gesammelte Werke,
vol. 4, p. 501) mais diffère entièrement de celui que Jacobi
qualifie de canonique dans «Nova methodus aeq. diff. partiales
primi ordinis integrandi » (J. de Crelles tome 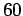 p.
p. 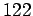 , cf Jacobi, g. Werke, vol. 5 p. 128). B.
, cf Jacobi, g. Werke, vol. 5 p. 128). B.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... consid\'er\'e.4
- On reconnaît ici ce que Ritt
désignait comme «l'analogue différentiel du
théorème de Bézout». N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline1972#5
- Il s'agit de ce que nous
appellerions les différentielles de Kaehler:
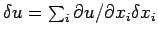 , qui donnent le linéarisé
tangeant. N.d.T.
, qui donnent le linéarisé
tangeant. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... constants6
- Cette affirmation ne peut tenir
que pour le cas générique; encore est-elle loin d'être
immédiate. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... expression7
- Cette notation désigne la forme de
l'expression et non sa valeur particulière. Ainsi, les coefficients
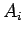 sont a priori différents dans
sont a priori différents dans 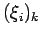 et
et
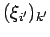 intervenant dans
intervenant dans 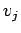 et
et 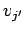 avec
avec
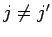 , me si
, me si 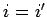 et
et 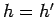 . N.d.T.
. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
d\'esigne8
- Même remarque pour
![$[\lambda]_{m}$](img42.png) qu'à la note
5 pour
qu'à la note
5 pour 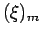 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... diminue9
- Jacobi se montre ici plus précis que dans la
proposition II, puisqu'il affirme que l'ordre est toujours
inférieur à
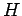 si le déterminant s'annule. Ritt semblait
douter que cette borne soit valable en dehors du cas
générique où le déterminant est non nul (cf J.F. Ritt, Differential algebra, AMS, New York, 1950, p. 136),
mais l'exemple de Ritt (loc. cit. p. 140) prend pour
hypothèse l'ordre de deux composantes et non l'ordre des
polynômes qui les définissent. La borne de Jacobi demeure
toutefois conjecturale. N.d.T.
si le déterminant s'annule. Ritt semblait
douter que cette borne soit valable en dehors du cas
générique où le déterminant est non nul (cf J.F. Ritt, Differential algebra, AMS, New York, 1950, p. 136),
mais l'exemple de Ritt (loc. cit. p. 140) prend pour
hypothèse l'ordre de deux composantes et non l'ordre des
polynômes qui les définissent. La borne de Jacobi demeure
toutefois conjecturale. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... effectu\'ee10
- Voir «De
aequationum differentialum systemate non normali ad formam normalem
revocando», publié par A. Clebsch, C.G.J. Jacobi's
gesammelte Werke, fünfter Band, herausgegeben von K. Weierstrass,
Berlin, Bruck und Verlag von Georg Reimer, 1890, p. 485-513. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tableau11
- Nous dirions sans doute aujourd'hui matrice,
mais le terme n'a été introduit qu'en 1850 par Sylvester,
c'est-à-dire approximativement au moment de la rédaction de cet
article posthume, Jacobi étant mort en 1851 (cf Dieudonné,
Abrégé d'histoire des mathématiques, Hermann, Paris, 1978,
p. 96. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ensembles12
- Malgré son anachronisme,
«ensemble » a été utilisé pour traduire
complexus. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
s\'erie13
- Celle contenant le maximum en
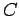 . N.d.T.
. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
s\'erie14
- Contenant
 . N.d.T.
. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transversaux15
- Voir
ci-dessus la définition de la troisième
classe page
![[*]](/usr/share/latex2html/icons/crossref.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...#tex2html_wrap_inline2936#16
- Le texte d'origine
comporte ici
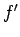 au lieu de
au lieu de 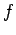 , ce qui ne fait pas sens: une
probable erreur typographique. N.d.T.
, ce qui ne fait pas sens: une
probable erreur typographique. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.