DÉFINITION 1. -- Supposant connu le vecteur de paramètres ![]() , on dit qu'un
système différentiel est observable si l'application
, on dit qu'un
système différentiel est observable si l'application ![]() qui associe aux conditions initiales
qui associe aux conditions initiales ![]() la fonction de sortie
la fonction de sortie ![]() admet un inverse à gauche.
admet un inverse à gauche.
Cette propriété peut être testée par le critère de Kalman suivant.
THÉORÈME 2. -- Un système est observable ssi la matrice
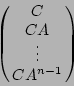
On a ![]() ,
,
![]() , ...,
, ...,
![]() , ... On peut supprimer les
termes dépendant de
, ... On peut supprimer les
termes dépendant de ![]() et de ses dérivées, qui sont
connus. On connaît donc
et de ses dérivées, qui sont
connus. On connaît donc ![]() ,
, ![]() , etc. D'après le
théorème de Cayley-Hamilton,
, etc. D'après le
théorème de Cayley-Hamilton, ![]() ,
, ![]() , ce qui
implique que les puissances de
, ce qui
implique que les puissances de ![]() s'expriment toutes à partir de
celles de degré inférieur à
s'expriment toutes à partir de
celles de degré inférieur à ![]() . La valeur de
. La valeur de ![]() peut
donc être déterminé de manière unique si et seulement
si le système
peut
donc être déterminé de manière unique si et seulement
si le système
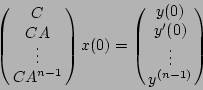
On voit que l'on peut plus généralement calculer ![]() ,
connaissant les dérivées de
,
connaissant les dérivées de ![]() au temps
au temps ![]() . Ceci ne fournit
en pratique qu'une méthode médiocre d'observation,
c'est-à-dire de calcul de l'état. En effet, les mesures sont
souvent perturbées par des bruits, ce qui rend de plus en
plus imprécise l'évaluation des dérivées par
différence finie à mesure que l'ordre croît.
. Ceci ne fournit
en pratique qu'une méthode médiocre d'observation,
c'est-à-dire de calcul de l'état. En effet, les mesures sont
souvent perturbées par des bruits, ce qui rend de plus en
plus imprécise l'évaluation des dérivées par
différence finie à mesure que l'ordre croît.