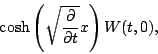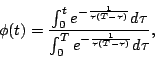suivant: Discrétisations
monter: Sixième séance. Systèmes d'équations
précédent: Sixième séance. Systèmes d'équations
Le cas le plus simple est celui de l'équation de la chaleur. On
considère une tige conductrice, de longueur 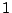 , isolée au
point
, isolée au
point 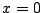 et chauffée à une température
et chauffée à une température 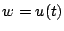 au
point
au
point 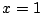 . Le système est donc décrit par l'équation
. Le système est donc décrit par l'équation
avec les conditions aux bords 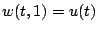 , et
, et 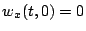 (on
utilisera par la suite cette notation pour les dérivées
partielles).
(on
utilisera par la suite cette notation pour les dérivées
partielles).
L'idée de base est de traiter l'opérateur
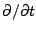 comme une constante
comme une constante 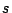 . Celle-ci est inspirée par la
transformation de Laplace, mais on peut l'utiliser comme un
intermédiaire de calcul, un peut comme les nombres imaginaires.
. Celle-ci est inspirée par la
transformation de Laplace, mais on peut l'utiliser comme un
intermédiaire de calcul, un peut comme les nombres imaginaires.
On sait résoudre l'équation
la forme générale des solutions est
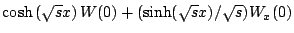 .
Si l'on remplace maintenant
.
Si l'on remplace maintenant 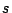 par
par
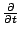 , on
obtient bien des solutions à partir des développement en
séries de
, on
obtient bien des solutions à partir des développement en
séries de 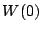 et
et 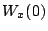 . Le terme
. Le terme
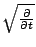 n'apparaît pas, car les
fonctions
n'apparaît pas, car les
fonctions 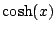 et
et
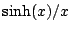 sont paires. Dans le cas qui nous
occupe, on obtient une solution
sont paires. Dans le cas qui nous
occupe, on obtient une solution
et l'on peut donc paramétrer les trajectoires du système en
choisissant arbitrairement la fonction 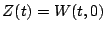 , pourvu que le
développement en série converge. On peut bien sûr choisir une
fonction analytique, mais il suffit d'avoir
, pourvu que le
développement en série converge. On peut bien sûr choisir une
fonction analytique, mais il suffit d'avoir
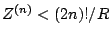 pour que
la série en espace ait un rayon de convergence
pour que
la série en espace ait un rayon de convergence 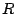 non nul. Une
fonction satisfaisant cette propriété est dite Gevrey d'ordre
non nul. Une
fonction satisfaisant cette propriété est dite Gevrey d'ordre
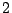 . Ceci permet d'utiliser la fonction
. Ceci permet d'utiliser la fonction
qui permet d'amener la tige de la température uniforme
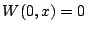 , à la température uniforme
, à la température uniforme 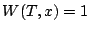 en un temps
fini
en un temps
fini 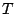 , ce qui est impossible avec des fonctions analytique, qui ne
peuvent être non nulles tout en ayant toutes leurs
dérivées nulles en un point.
, ce qui est impossible avec des fonctions analytique, qui ne
peuvent être non nulles tout en ayant toutes leurs
dérivées nulles en un point.
Cette méthode a été appliquée avec succès à de nombreux systèmes
physiques: bras de grue flexibles, cables pesants, récipients
contenant des liquides. Il faut naturellement faire des hypothèses
permettant de se ramener à un système linéaire possédant des solutions
explicites. Lorsque les modèles deviennent complexes, l'utilisation du
calcul formel est une aide appréciable pour simplifier la
manipulation des formules, et surtout éviter les erreurs.



suivant: Discrétisations
monter: Sixième séance. Systèmes d'équations
précédent: Sixième séance. Systèmes d'équations
Francois Ollivier
2005-02-01
![]() , isolée au
point
, isolée au
point ![]() et chauffée à une température
et chauffée à une température ![]() au
point
au
point ![]() . Le système est donc décrit par l'équation
. Le système est donc décrit par l'équation
![]() comme une constante
comme une constante ![]() . Celle-ci est inspirée par la
transformation de Laplace, mais on peut l'utiliser comme un
intermédiaire de calcul, un peut comme les nombres imaginaires.
. Celle-ci est inspirée par la
transformation de Laplace, mais on peut l'utiliser comme un
intermédiaire de calcul, un peut comme les nombres imaginaires.