Observateurs de Luenberger

On considère un système linéaire et l'on se propose de calculer l'état à partir de la sortie $y$, en supposant que le système est observable.

Pour celà, on va construire un état fictif ${\widehat x}$, solution de l'équation ${\widehat x}' = A{\widehat x}- Bu + MC{\widehat x}- My$. Ainsi, on aura $({\widehat x}- x) = (A - MC) ({\widehat x}-x)$.

PROPOSITION 22. -- Les coefficients du polynôme caractéristique de la matrices $A - MC$ s'expriment linéairement en fonction des coefficients de $M$.

On peut résoudre le système et fixer arbitrairement les coefficients du polynôme caractéristique ssi le système est observable.PREUVE. -- Plaçons-nous pour simplifier dans le cas d'une seule sortie $y$. Si le système est observable, on peut prendre pour nouvel état du système $y$, $y'$, ..., $y^{(n-1)}$. La matrice $A$ est dans une telle base de la forme

$$\left(\matrix{0 & 1 & 0 &\cdots & 0\cr \vdots&\ddots&\ddots... ...0 & 1\cr - a_{0} &-a_{1} &\cdots &-a_{n-2} &-a_{n-1}}\right),$$

Les $a_{i}$ étant les coefficients du polynôme caractéristique. En choisissant une nouvelle base $z_{1}=y$, $z_{2}= y'-a_{n-1}y$, $z_{3}=y''-a_{n-1}y'-a_{n-2}y$, ..., $z_{n}=y^{(n-1)}-a_{n-1}y^{(n-2)}-\cdots-a_{1}y$, la matrice prend cette fois la forme

$$\left(\matrix{-a_{0}& 1 & 0 &\cdots & 0\cr -a_{1}& 0 &\ddot... ..._{n-2}&0 &\cdots &0 & 1\cr -a_{n-1}&0 &\cdots &0 & 0}\right),$$

et dans cette nouvelle base, où $C=(\matrix{1 & 0 &\cdots & 0})$, le polynôme caractéristique de $A + MC$ aura pour coefficients les $a_{i}+b_{i}$ si $M=(\matrix{b_{0} &\cdots & b_{n-1}})$.

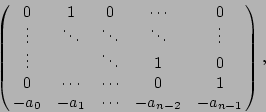
Ceci prouve que l'on peut assigner les valeurs propres si le système est observable. S'il ne l'est pas, on peut factoriser $\chi_{A+MC}$ en un produit $PQ$, où les coefficients du premier facteur, de degré égal à la dimension $r$ de l'espace vectoriel engendré par la sortie $y$ et ses dérivées peuvent être choisis arbitrairement en fonction de $M$, et où le second facteur $Q$ est indépendant de $M$. La preuve, élémentaire, est laissée au lecteur.    height .9ex width .8ex depth -.1ex

Ceci nous permet de construire un observateur en choisissant les coefficients de manière à ce que les valeurs propres soient toutes à partie réelle strictement négative. Ainsi, asymptotiquement, ${\widehat x}$ tend vers $x$. Si l'on prend des parties réelles faiblement négative, la convergence sera plus lente, mais le résultat moins sensible au bruit, qui sera « moyenné» il y a un compromis à faire entre vitesse de convergence et précision.

Ce type d'observateur a été proposé par David G. Luenberger en 1966, dans le cas général, le cas d'une seule sortie ayant été publié dès 1964.

Cette méthode supose de connaître avec une très bonne précision les coefficients du système, car les valeurs propres sont très sensibles aux variation des coefficients du polynôme caractéristique. Considérons en effet le polynôme de Wilkinson $(x+1)(x+2)\cdots(x+20)=x^{20}+210x^{19}+\cdots20!$, il suffit d'ajouter $2^{-32}$ au terme de degré $19$ de W, pour que le nouveau polynôme n'ait plus que $16$ racines réelles. Celles-ci sont heureusement toutes à partie réelle strictement négatives. Mais si l'on prend $(x+5)^{10} + 0,5x^{9}$ au lieu de $(x+5)^{10}$, les parties réelles des racines vont de $-16,8588$ à $-2,7108$. Bien que l'on se soit seulement trompé de $1\%$ sur la valeur du premier coefficient, les valeurs propres varient elles de $-50\%$ à $+200\%$!

Or, il n'est pas suffisant d'avoir un processus qui converge, il faut que celui-ci le fasse assez vite, pour pouvoir disposer à temps d'une évaluation correcte de l'état, mais pas trop, de manière à avoir un résultat peu sensible au bruit. Le choix des valeurs est donc le résultat d'un compromis délicat, qui devient très aléatoire si les valeurs des coefficients sont trop incertaines.

On peut, si l'on dispose de $r$ sorties indépendantes, construire un observateur d'ordre $n-r$ seulement. En effet, tel que nous l'avons décrit, l'observateur recalcule la valeur de la sortie. Ceci n'est pas nécessairement un inconvénient, car la valeur recalculée peut être meilleure que celle d'origine, bruitée.