Quelques autres critères de platitude

La première apparition d'une notion apparentée aux systèmes plats a été retrouvée dans un article de David Hilbert en 1912, sous le nom de «integralloss system», c'est-à-dire de système dont les solutions peuvent être exprimées sans intégration. En 1915, Élie Cartan en a donné la caractérisation suivante dans un cas particulier, qui correspond pour l'automatique contemporaine à celui de systèmes à deux commandes sans dérives, c'est-à-dire de la forme:

$$x_{i}' = f_{i}(x)u + g_{i}(x)v.$$

Les deux commandes sont $u$ et $v$, et le système est dit sans dérive car $x'=0$ lorsque les dérivées sont nulles. Le champ des vitesse est une combinaison linéaires des deux champs (ou dérivations) $\delta_{1}= \sum_{i=1}^{n} f_{i}(x)\partial/\partial x_{i}$ et $\delta_{2}= \sum_{i=1}^{n} g_{i}(x)\partial/\partial x_{i}$.

THÉORÈME 19. -- Considérons un système sans dérive. On définit les espaces vectoriels $E_{i}$ comme suit : $E_{0}=\langle \delta_{1}, \delta_{2}\rangle$, ... $E_{i+1}=\langle [a,b] \vert (a,b)\in E_{i}^{2}\rangle$. Un système à deux commande sans dérive est plat ssi pour tout $0\le i\le n-3$, l'espace vectoriel $E_{i}$ est de dimension $i+2$Cette condition est trivialement satisfaite pour $n\le 4$. Le cas $n=3$ correspond à l'exemple de la voiture, $n=4$ à celui d'un camion avec remorque.

THÉORÈME 20. -- Un système sans dérive

$$x_{i}' = \sum_{j=1}^{n-1} f_{j,i}(x) u_{j}$$

avec un état de dimension $n$ et $n-1$ commandes est plat ssi il est commandable.

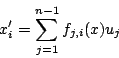
Nous ne détaillons pas la preuve, nous contentant décrire comment on peut obtenir des sorties linéarisantes. Posons $\delta_{j}=\sum_{i=1}^{n} f_{j,i} \partial/\partial x_{i}$. Soient $C_{1}(x)$, ..., $C_{n-1}(x)$, $n-1$ fonctions de l'état. On considère la dérivation $\delta=\sum_{i=1}^{n-1} C_{i}{\partial/\partial u_{1}}$. On prend pour $z_{1}$, ..., $z_{n-1}$, $n-1$ solution fonctionnellement indépendantes de l'équation aux dérivées partielles linéaire $[\delta,d/dt]=0$. Celles-ci forment alors (pour un choix « générique» des $C_{i}$) une sortie linéarisante, car $\sum_{i=1}^{n-1}(\partial/\partial u_{i})z_{i}'=0$, ce qui montre que la matrice jacobienne $(\partial z_{i}'/\partial u_{j})$ n'est pas de rang maximal $n-1$, ce qui permet d'exprimer localement l'état $x$, connaissant $z$ et $z'$, si

$$\hbox{rang}\left(\matrix{{\partial z'\over \partial u}&{\par... ... \hbox{rang}\left(\matrix{\partial z'/\partial u }\right) = n,$$

c'est-à-dire si la première matrice est de rang maximal. Si ce n'est pas le cas, les $z_{i}$ forment eux-même l'état d'un système à $n-2$ commandes, pour lequel on peut chercher une sortie plate. Cette sortie plate sera complétée d'une variable d'état $x_{i}$ pour former une sortie linéarisante du système de départ. Ceci ne peut arriver que pour $n\ge 3$, car sinon, $z'$ serait nul, ce qui contredit la contrôlabilité.

Exemple 21. -- La voiture est un bon exemple. Si l'on prend $\delta=\partial/\partial u$, on obtient aisément comme solution $z_{1}=y$ et $z_{2}=e^{x}{\rm tan}(\alpha/2)$. Ce type de solution présente l'inconvénient de n'être pas invariante par le groupe des translations et des rotations. Or, on souhaite un contrôle qui ne dépende pas du choix des coordonnées.

Pour cela, il faut prendre un champs $\delta$ dont l'expression soit invariante par le groupe: $\delta= \cos(\alpha+\phi)\partial/\partial u + \sin(\alpha+\phi)\partial/\partial v$. Pour $\phi\neq 0$, on obtient des sorties linéarisantes qui correspondent aux coordonnées d'un point de l'essieu arrière (l'intersection de la droite d'angle $\phi+\pi/2$ dans le référentiel du véhicule passant par le point de référence choisi sur celui-ci. Quand $\phi$ tend vers $0$, ce point d'intersection tend vers l'infini. On obtient alors des sorties linéarisantes $z_{1}=\alpha$ et $z_{2}=\cos(\alpha)y-\sin(\alpha)x$. Celles-ci ne sont plus préservées que par les rotations par rapport à l'origine.

Détailler les calculs est un excellent exercice.