Fast spherical drawing of triangulations

Balanced Schnyder woods for planar triangulations: an experimental study with applications to graph drawing and graph separators

(Luca Castelli Aleardi, Ecole Polytechnique, presented at the 27th. Int. Symp. on Graph Drawing 2019)

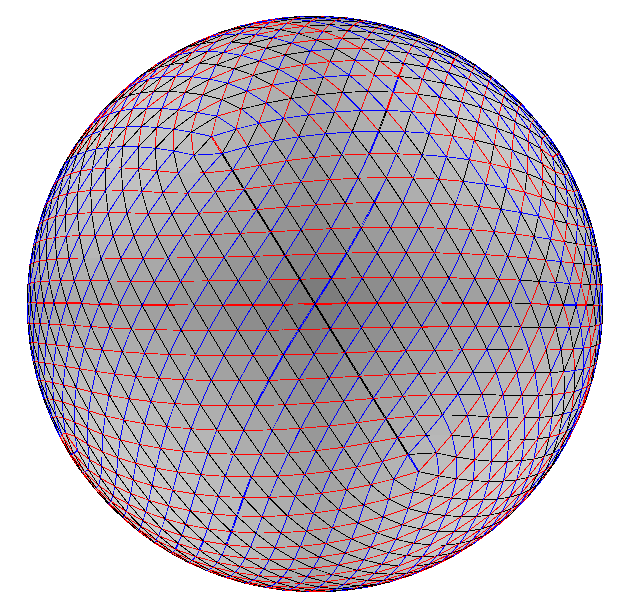
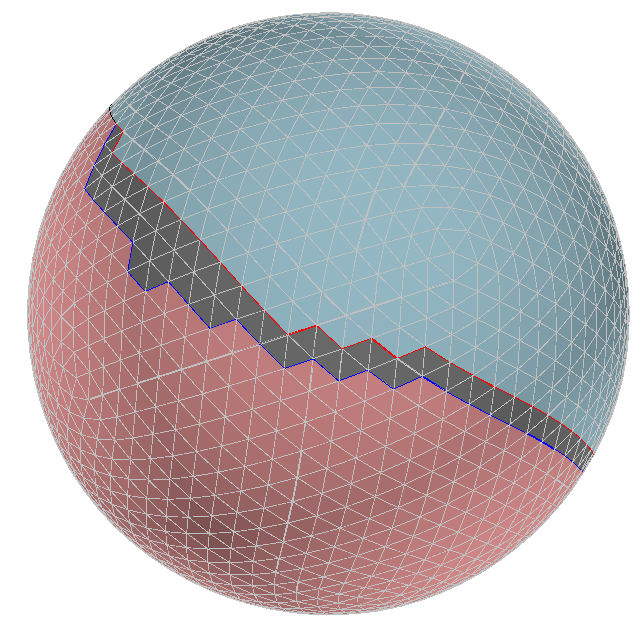
Computation of Schnyder woods

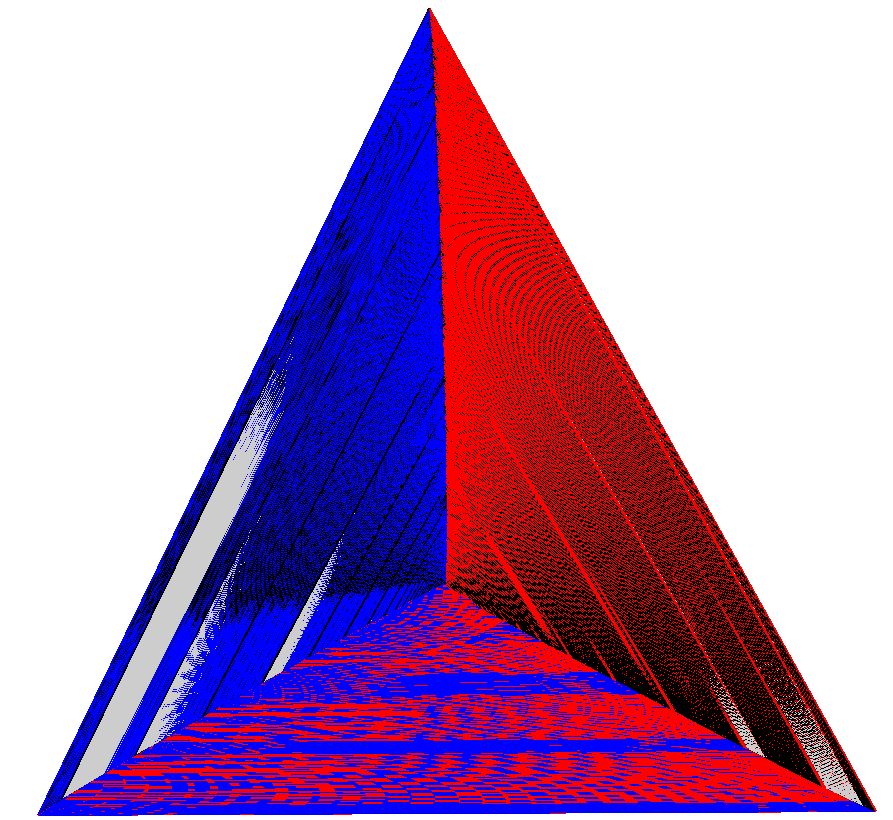
Balanced Schnyder wood of the sphere graph (2562 vertices): its corresponding short separator and Schnyder drawing. Minimal Schnyder wood and its corresponding Schnyder drawing.

In this work we consider balanced Schnyder woods for planar graphs, which are Schnyder woods where the number of incoming edges of each color at each vertex is balanced as much as possible. We provide a simple linear-time heuristic allowing us to obtain well balanced Schnyder woods in practice. As test applications we consider two important algorithmic problems: the computation of Schnyder drawings and the computation of small cycle separators.
While not being able to provide theoretical guarantees, our experimental results (on a wide collection of planar graphs) suggest that the use of balanced Schnyder woods leads to an improvement of the quality of the layout of Schnyder drawings, and provides an efficient tool for computing short and balanced cycle separators.

Data sets (genus 0 triangulations with no boundaries, stored in OFF format)

mesh graphs (3D meshes in OFF format, from the aim@shape and Thingi10K repositories) synthetic graphs (sphere, globe, cylinder, thin cylinder) random triangulations (endowed with a Schnyder planar embedding) delaunay graphs (of random points in unit circle)
	mesh and synthetic graphs

Computation of balanced and minimal Schnyder woods, Schnyder drawings and short separators for planar triangulations

Files to download (for running tests and benchmarks: Java 1.8 required): the .jar files below include all required java libraries (e.g. Processing for 3D rendering)

SchnyderLayoutComputation.jar (compiled with Java 1.8): a runnable .jar file for the computation of Schnyder drawings (with 3D rendering)
SchnyderShortSeparatorComputation.jar (compiled with Java 1.8): a runnable .jar file for the computation of balanced Schnyder woods and short simple cycle separators (with 3D rendering)
FastSchnyderComputation.jar (compiled with Java 1.8): a fast implementation of all algorithms, for performing benchs and evaluating the runtime performances of all algorithms involving Schnyder woods

Usage example (running from a Terminal): 1 or 2 parameters are required (input file in OFF format, initial seed: index of the root half-edge)

java -jar SchnyderLayoutComputation.jar sphere12k.off 100 (3D rendering available only for meshes with up to 300000 vertices)

java -jar SchnyderShortSeparatorComputation.jar sphere12k.off 100 (3D rendering available only for meshes with up to 300000 vertices)

java -Xms4G -Xmx4G -jar FastSchnyderComputation.jar horse1.off (for computing statistics and runtime performances: tests are repeated with 100 initial random seeds)


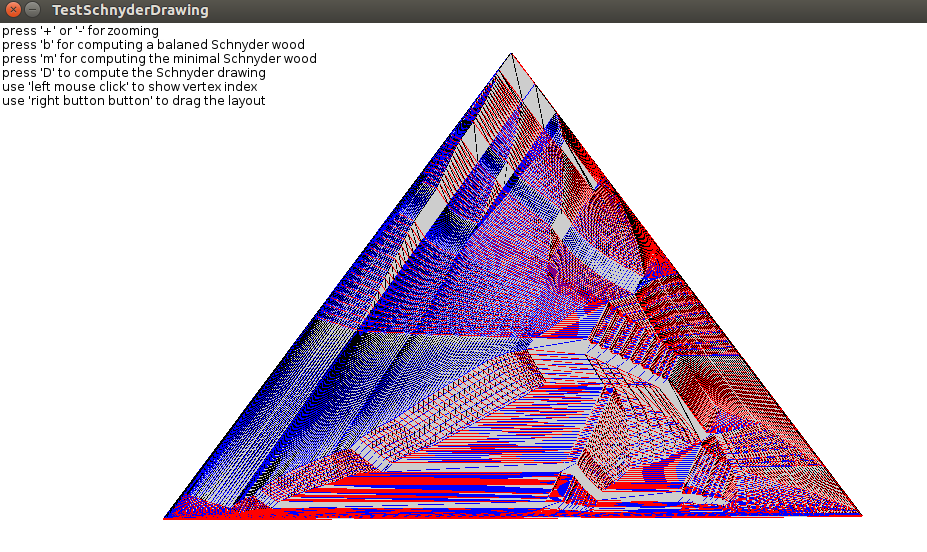
Press 'b' for computing balanced Schnyder woods (press 'm' for the minimal one)	press 'D' for computing the Schnyder drawing

Output example 1 (computation of a Schnyder drawing):

Schnyder drawing computation (Ecole Polytechnique, 2019)
Reading a collection of polygonal faces from OFF format (shared vertex representation): /home/amturing/Desktop/doc/datasets/OFF/Synthetic/sphere12k.off
	Reading vertices...done 12962 vertices
	Reading face degrees...done 25920 faces
Triangle soup loaded from from OFF file (0.909854272 seconds)
Building a (pointer based) halfedge representation of a surface mesh...done (0.063991961 seconds)
Checking Polyhedron...ok
Closed mesh: no boundaries
The mesh is pure triangle
n: 12962  e: 38880  f: 25920  b:0  genus: 0
Checking Polyhedron...ok
Closed mesh: no boundaries
The mesh is pure triangle
n: 12962  e: 38880  f: 25920  b:0  genus: 0
Initialize Schnyder wood computation: 	 root face (v3932, v4355, v8252)	 root edge e100 (v3932, v4355)
Schnyder wood computed
Schnyder drawing initialization...done (memory usage: 47 MBytes)
Computing the size of subtrees in T0...done
Computing the height of nodes in the tree T0...done
Computing the height of nodes in the tree T1...done
Computing the height of nodes in the tree T2...done
max length=1.4142135623730951, avg length=0.01871947752984827, edge length aesthetic=0.9912204024607774
f= 25919.0
n= 12962

Output example 2 (fast computation of simple cycle separators):

Fast computation of Schnyder woods and simple cycle separators (Ecole Polytechnique, 2019)
Reading a collection of polygonal faces from OFF format (shared vertex representation): /home/amturing/Desktop/doc/datasets/OFF/LargePlanarTri/horse1.off
	Reading vertices...done 20000 vertices
	Reading face degrees...done 39996 faces
Triangle soup loaded from from OFF file (1.074451719 seconds)
Building a (pointer based) halfedge representation of a surface mesh...done (0.0845149 seconds)
Checking Polyhedron...ok
Closed mesh: no boundaries
The mesh is pure triangle
n: 20000  e: 59994  f: 39996  b:0  genus: 0
Creating an array based half edge DS from a Polyhedron...done (0.029173073 s, 19 MBytes)
Running warming phase...done

Running runtime benchmarks

--- Starting test 1 ---
Running garbage collector...done
Schnyder wood initialization: 	 root face (v5348, v5347, v10420)	 root edge e6144 (v5348, v5347)
Fast computation of a balanced Schnyder wood...done (0.005126275 seconds)
Schnyder drawing initialization...done (memory usage: 20 MBytes)
Fast computation of the Schnyder drawing...done (0.00669152 seconds)
Computing shortest balanced separator...done (3.87792E-4 seconds)
Separator statistics:
	best vertex: v16361
	sqrt(8.0m)=692 sqrt(8.0n)=400, sqrt(m)=244, sqrt(n)=141
	boundary size: 173
	normalized boundary size: 0.706 sqrt(m)
	normalized boundary size: 0.432 sqrt(8n)
	separator balance: 6737 (0.336 n)
--- end of test 1 ---



..........
..........
..........
..........



--- Starting test 100 ---
Running garbage collector...done
Schnyder wood initialization: 	 root face (v718, v720, v16136)	 root edge e735 (v718, v720)
Fast computation of a balanced Schnyder wood...done (0.00483866 seconds)
Schnyder drawing initialization...done (memory usage: 20 MBytes)
Fast computation of the Schnyder drawing...done (0.01222462 seconds)
Computing shortest balanced separator...done (3.59825E-4 seconds)
Separator statistics:
	best vertex: v3179
	sqrt(8.0m)=692 sqrt(8.0n)=400, sqrt(m)=244, sqrt(n)=141
	boundary size: 159
	normalized boundary size: 0.649 sqrt(m)
	normalized boundary size: 0.397 sqrt(8n)
	separator balance: 9492 (0.474 n)
--- end of test 100 ---

--- Runtime time performances (results expressed in seconds) ---
	Number of tests: 100
	minimum=0.0108
	maximum=0.0286
	median=0.0123


Balanced Schnyder wood of the sphere graph (2562 vertices): its corresponding short separator and Schnyder drawing.	Minimal Schnyder wood and its corresponding Schnyder drawing.