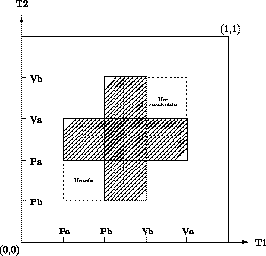
Figure 1: Example of a progress graph



Figure 1: Example of a progress graph
The shaded area represents states which are not allowed in any execution path, since they correspond to mutual exclusion. Such states constitute the forbidden area. An execution path is a path from the initial state (0,...,0) to the final state (1,...,1) avoiding the forbidden area and increasing in each coordinate - time cannot run backwards. We call these paths directed paths or dipaths. This entails that paths reaching the states in the dashed square underneath the forbidden region, marked ``unsafe'' are deemed to deadlock, i.e. they cannot possibly reach the allowed terminal state which is (1,1) here. Similarly, by reversing the direction of time, the states in the square above the forbidden region, marked ``unreachable'', cannot be reached from the initial state, which is (0,0) here. Also notice that all terminating paths above the forbidden region are ``equivalent'' in some sense, given that they are all characterized by the fact that T2 gets a and b before T1 (as far as resources are concerned, we call this a schedule). Similarly, all paths below the forbidden region are characterized by the fact that T1 gets a and b before T2 does.
Figure 2: The corresponding request graph
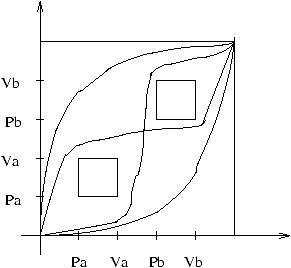
Figure 3: The progress graph corresponding to Pa. Va. Pb. Vb | Pa. Va. Pb. Vb
There is another method to determine deadlocks in such situations, which was of course known long ago and was entirely graph-theoretic, known as the request graph. Figure 2 depicts the request graph corresponding to the progress graph of Figure 1. Nodes of this graph are resources of the concurrent system, i.e. here, semaphores. There is an oriented edge from a resource x to a resource y if there is a process which has locked x and needs to lock y at a given time. A sufficient condition for such systems to be deadlock-free is that their corresponding request graphs be acyclic3 . Unfortunately, this is not a necessary condition in general. For instance a request graph cannot capture the notion of n-semaphores, i.e. resources that can be shared by up to n processes but not n+1 (for instance, asynchronous buffers of communication of size n which can be ``written'' on by at most n processes). This in fact really calls for some higher-dimensional versions of graphs.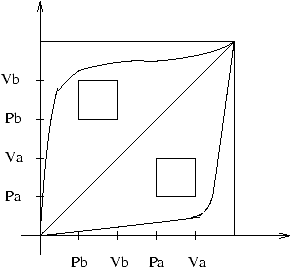
Figure 4: The progress graph corresponding to Pb. Vb. Pa. Va | Pa. Va. Pb. Vb

