L'ordre d'un système de
Publié par A. Clebsch d'après les manuscrits posthumes
de l'ill. C.G.J. Jacobi.2
to to 2cm
Dans mon article «Théorie du dernier multiplicateur »3, j'ai déterminé le multiplicateur des équations différentielles isopérimétriques c'est-à-dire qui se rapportent au problème isopérimétrique consistant à rendre nulle la variation d'une intégrale donnée, dépendant d'une variable indépendante et de plusieurs variables dépendantes.
J'ai montré que cette détermination était exposée à de grandes et multiples difficultés si les dérivées les plus hautes des variables dépendantes intervenant dans l'intégrale donnée ne sont pas du même ordre.
Dans ce cas, le système d'équations différentielles isopérimétriques ne sera pas dans une forme telle que les dérivées les plus hautes de chacunes des variables dépendantes peuvent être prises pour des inconnues dont les valeurs seront déterminées par les équations elles-mêmes.
On ramènera alors les équations différentielles isopérimétriques à la forme que j'ai indiquée seulement après certaines dérivations et éliminations ; ceci rend compliquée la recherche de la valeur du multiplicateur.
En récompense de ce travail, j'ai obtenu tout le matériel nécessaire pour exposer avec soin la réduction en forme normale d'un système non normal d'équations différentielles. Dans cette recherche, je suis parvenu à des propositions générales que l'on verra combler certaines lacunes de la théorie des équations différentielles ordinaires et dont je vais ici indiquer brièvement l'essentiel.
Nous appelons la variable indépendante ![]() , ses fonctions -- ou
variables considérées comme dépendantes --
, ses fonctions -- ou
variables considérées comme dépendantes --
![]() . Soient entre ces variables
. Soient entre ces variables ![]() équations
différentielles :
équations
différentielles :
=
by -1cm
= 1 1cm
1) l'ordre du système d'équations différentielles
proposées, ou bien encore le nombre de constantes arbitraires que
réclame leur intégration complète, est égal au maximum
qu'atteignent toutes les sommes :
Je désignerai par ![]() ce maximum, ou ordre du système ;
ce maximum, ou ordre du système ; ![]() sera
égal à la somme des ordres des dérivées les plus hautes de
chacunes des variables qui apparaissent dans le système normal
auquel le système proposé peut être réduit. Ce même
nombre
sera
égal à la somme des ordres des dérivées les plus hautes de
chacunes des variables qui apparaissent dans le système normal
auquel le système proposé peut être réduit. Ce même
nombre ![]() sera inférieur à la somme formée de la même
manière respectivement au système proposé.
sera inférieur à la somme formée de la même
manière respectivement au système proposé.
Il existe différentes formes normales -- et toujours au moins deux4-- auxquelles le système proposé peut être réduit ; ces réductions ne s'effectuant pas sans l'aide de diverses dérivations et éliminations. Dans ce domaine, cette proposition est fondamentale :
= by -1cm = 1 1cm 2) parmi les diverses manières de dériver les équations différentielles proposées pour que naissent des équations auxiliaires à l'aide desquelles le système proposé puisse être réduit en forme normale par des éliminations seules, il existe une manière unique qui requiert le moins de dérivations, car de n'importe quelle autre manière, certaines des équations différentielles proposées, ou toutes, doivent être dérivées un plus grand nombre de fois successives, tandis qu'il ne peut se faire d'aucune autre manière que l'une des équations différentielles proposées soit dérivée moins de fois.
Nous désignons cette manière la plus rapide sous le nom de
réduction la plus brève. Dans cette réduction, il y aura
toujours une ou plusieurs des équations différentielles
proposées qui ne seront pas dérivées du tout, c'est-à-dire
telles qu'aucune de leurs dérivées ne contribue au système
d'équations auxiliaires. Donc, si nous supposons que pour former les
équations auxiliaires, l'équation ![]() doit être
dérivée
doit être
dérivée ![]() fois de suite, parmi les nombres entiers non
négatifs :
fois de suite, parmi les nombres entiers non
négatifs :
«Étant données ![]() quantités
quantités ![]() quelconques,
où
quelconques,
où ![]() et
et ![]() doivent prendre les valeurs
doivent prendre les valeurs ![]() ,
rechercher
,
rechercher ![]() quantités positives ou nulles minimales
quantités positives ou nulles minimales
![]() telles que, en
posant
telles que, en
posant
![]() on puisse parmi les
on puisse parmi les ![]() quantités
quantités ![]() choisir
choisir ![]() quantités :
quantités :
J'indiquerai brièvement les principales étapes de la solution du
problème proposé. Disposons les quantités ![]() en un
tableau carré :
en un
tableau carré :
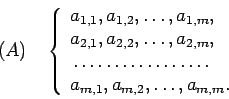
Si l'on trouve une série horizontale dont aucun terme n'est maximum (par ce terme, j'entendrai toujours ici qu'il n'est inférieur à aucun des autres termes) parmi tous ceux de la même verticale, j'ajoute à tous les termes de cette série horizontale une même quantité positive et de valeur minimale pour que l'un de ses termes devienne égal au maximum de sa verticale.
Après la
préparation indiquée, si l'on a changé le carré proposé en
le suivant :
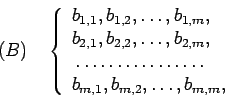
J'appelle
système de maxima transversaux un système de
quantitées ![]() qui sont placées dans des séries
horizontales et verticales toutes différentes et dont chacune est
maximale parmi toutes les quantités placées dans la même
verticale.
qui sont placées dans des séries
horizontales et verticales toutes différentes et dont chacune est
maximale parmi toutes les quantités placées dans la même
verticale.
Je prends dans le carré ![]() le nombre maximal de
maxima transversaux, et quand le même nombre apparaît de
plusieurs manières, je choisis arbitrairement l'un des systèmes,
dont je marque les termes d'un astérisque. Le nombre maximal de ces
maxima transversaux peut être ou
le nombre maximal de
maxima transversaux, et quand le même nombre apparaît de
plusieurs manières, je choisis arbitrairement l'un des systèmes,
dont je marque les termes d'un astérisque. Le nombre maximal de ces
maxima transversaux peut être ou ![]() 5 ou
5 ou ![]() etc. ou
etc. ou ![]() ; si leur nombre est
; si leur nombre est ![]() , le problème proposé est
résolu. Si ce nombre est plus petit que
, le problème proposé est
résolu. Si ce nombre est plus petit que ![]() , je fait en sorte
d'augmenter certaines des séries horizontales de nombres minimaux
tels que dans le nouveau carré obtenu, le nombre de maxima
transversaux se trouve augmenté. En répétant ce processus, on
parviendra nécessairement à un carré dans lequel le nombre de
maxima transversaux est
, je fait en sorte
d'augmenter certaines des séries horizontales de nombres minimaux
tels que dans le nouveau carré obtenu, le nombre de maxima
transversaux se trouve augmenté. En répétant ce processus, on
parviendra nécessairement à un carré dans lequel le nombre de
maxima transversaux est ![]() ; l'ayant obtenu, la solution du
problème est trouvée. Je dis ici qu'une série horizontale
est augmentée, si une même quantité positive est ajoutée à
chacun de ces termes.
; l'ayant obtenu, la solution du
problème est trouvée. Je dis ici qu'une série horizontale
est augmentée, si une même quantité positive est ajoutée à
chacun de ces termes.
Les séries horizontales et verticales
auxquelles appartient le système de maxima transversaux choisis, je
les appelle séries ![]() et
et ![]() , et les autres séries horizontales
et verticales
, et les autres séries horizontales
et verticales ![]() et
et ![]() . Je note aussi d'un astérisque les termes maximaux dans une des verticales
de
. Je note aussi d'un astérisque les termes maximaux dans une des verticales
de ![]() . J'appelle maxima étoilés les termes
marqués d'un astérisque.
. J'appelle maxima étoilés les termes
marqués d'un astérisque.
Supposons que dans une série horizontale ![]() se trouve un
maximum étoilé auquel soit égal un terme d'une série
horizontale
se trouve un
maximum étoilé auquel soit égal un terme d'une série
horizontale ![]() placé dans la même verticales ; que dans la
série
placé dans la même verticales ; que dans la
série ![]() se trouve un maximum étoilé auquel est égal un
terme de la même verticale placé dans une série
horizontale
se trouve un maximum étoilé auquel est égal un
terme de la même verticale placé dans une série
horizontale ![]() , etc. Si de cette manière, on parvient à la
série horizontale
, etc. Si de cette manière, on parvient à la
série horizontale ![]() , où
, où ![]() désigne l'une des
séries
désigne l'une des
séries
![]() , je dirai que l'on passe
de
, je dirai que l'on passe
de ![]() à
à ![]() . Si l'on dit que l'on passe de
. Si l'on dit que l'on passe de ![]() à
à ![]() , la série
, la série ![]() et toutes les séries
intermédiaires
et toutes les séries
intermédiaires
![]() appartiennent
aux séries de
appartiennent
aux séries de ![]() ; la série
; la série ![]() peut appartenir aux
séries de
peut appartenir aux
séries de ![]() ou aux séries de
ou aux séries de ![]() . Si l'on ne peut
passer à une série de
. Si l'on ne peut
passer à une série de ![]() depuis une série horizontale
dans laquelle se trouve deux ou plusieurs maxima étoilés, et s'il
n'y a pas de terme d'une série de
depuis une série horizontale
dans laquelle se trouve deux ou plusieurs maxima étoilés, et s'il
n'y a pas de terme d'une série de ![]() maximal dans l'une
des séries de
maximal dans l'une
des séries de ![]() , ceci est un critère certifiant que le
nombre de maxima transversaux choisis est maximal.
, ceci est un critère certifiant que le
nombre de maxima transversaux choisis est maximal.
Ceci posé, je distribue toutes les séries horizontale en trois classes.
=
by -1cm = 1 1cm À la première
classe des séries horizontales, je rattache les séries dans
lesquelles se trouvent deux ou plusieurs maxima étoilés
ainsi que toutes les séries horizontales vers lesquelles on passe
depuis ces séries ; aucune des séries de la première classe
n'appartient à ![]() .
.
=
by -1cm = 1 1cm Je rattache à la deuxième classe des séries horizontales, celles n'appartenant pas
à la première, à partir desquelles on ne peut passer à l'une
des séries de ![]() .
.
=
by -1cm = 1 1cm Je rattache à la troisième classe des séries horizontales toutes les séries
de ![]() et les séries de
et les séries de ![]() à partir desquelles on peut
passer à une série de
à partir desquelles on peut
passer à une série de ![]() .
.
Cette répartition faite, j'augmente toutes les séries appartenant
à la troisième classe d'une quantité identique et minimale pour
que, leur étant ajoutée, l'un des termes de ces séries devienne
égal à l'un des maxima étoilés de la première ou de la
deuxième classe placé dans la même verticale. Si ce maximum
étoilé appartient à une série horizontale de la deuxième
classe, celle-ci, dans le nouveau carré obtenu, passe à la
troisième classe et il ne se produit pas d'autres changements dans
la répartition des séries6. Dans ce cas, l'opération doit
être itérée, la nouvelle série étant transférée de la
deuxième à la troisième classe et cela jusqu'à ce que l'un des
termes d'une série de la troisième classe ne devienne égal à
l'un des maxima étoilés d'une série de la première
classe. Ceci adviendra nécessairement lorsque toutes les séries
de la seconde classe seront passées dans la troisième, si cela ne
se produit pas avant. Nous obtenons ainsi en même temps un carré
dans lequel se trouve un plus grand nombre de maxima transversaux que
dans le carré ![]() . Alors, ayant de nouveaux réparti les maxima
étoilés et partagé les séries horizontales en trois classes,
un nouveau carré doit être formé par la même méthode, dans
lequel le nombre de maxima transversaux se trouvera de nouveau
augmenté en continuant jusqu'à ce que l'on parvienne à un
carré dans lequel on ait
. Alors, ayant de nouveaux réparti les maxima
étoilés et partagé les séries horizontales en trois classes,
un nouveau carré doit être formé par la même méthode, dans
lequel le nombre de maxima transversaux se trouvera de nouveau
augmenté en continuant jusqu'à ce que l'on parvienne à un
carré dans lequel on ait ![]() maxima transversaux. Le carré ainsi
trouvé sera dérivé du carré
maxima transversaux. Le carré ainsi
trouvé sera dérivé du carré ![]() proposé en ajoutant aux
séries horizontales des quantités positives minimales qui seront
les quantités cherchées
proposé en ajoutant aux
séries horizontales des quantités positives minimales qui seront
les quantités cherchées
![]() .
.
À cause de la complication de la règle, on s'aidera de la
présentation d'un unique exemple, contenu dans la figure suivante :
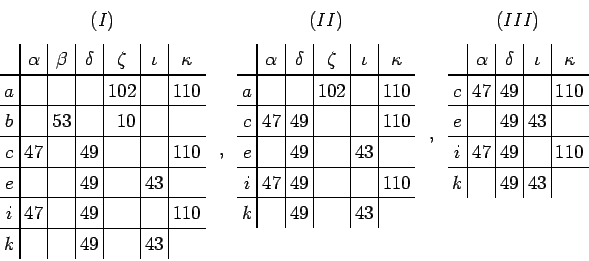
On considère le carré ![]() , dont j'ai souligné les termes
maximaux dans leur série verticale ; il en sera fait de même dans
les carrés dérivés. J'ai désigné les séries horizontales
par les lettres
, dont j'ai souligné les termes
maximaux dans leur série verticale ; il en sera fait de même dans
les carrés dérivés. J'ai désigné les séries horizontales
par les lettres
![]() . Notons que
. Notons que ![]() ne
contiennent aucun terme souligné. En soustrayant les termes de
ne
contiennent aucun terme souligné. En soustrayant les termes de ![]() des termes soulignés de leur verticale, on obtient les
différences :
des termes soulignés de leur verticale, on obtient les
différences :
![\begin{displaymath}
\begin{array}{c}
(B) \\ [\medskipamount]
\begin{array}{r\ver...
... &\hfill 59 &\hfill 4 &\hfill &\hfill 9
\end{array}\end{array}\end{displaymath}](img56.png)
Dans le carré ![]() , on peut affecter au plus six maxima
transversaux ; les séries verticales dans lesquelles ils sont
placés sont surmontées d'un
, on peut affecter au plus six maxima
transversaux ; les séries verticales dans lesquelles ils sont
placés sont surmontées d'un ![]() , les autres d'un
, les autres d'un ![]() . Je
note d'un astérisque ces mêmes maxima. Si dans l'une des séries
de
. Je
note d'un astérisque ces mêmes maxima. Si dans l'une des séries
de ![]() apparaît un terme souligné, je le note aussi
d'un astérisque. J'attache à la classe
apparaît un terme souligné, je le note aussi
d'un astérisque. J'attache à la classe ![]() les séries
les séries ![]() dans lesquelles apparaissent deux maxima étoilés ou plusieurs.
Dans les sept verticales auxquelles ces maxima appartiennent aucun
autre terme souligné n'apparaît, donc
dans lesquelles apparaissent deux maxima étoilés ou plusieurs.
Dans les sept verticales auxquelles ces maxima appartiennent aucun
autre terme souligné n'apparaît, donc ![]() et
et ![]() constituent seules la première classe. Les séries
constituent seules la première classe. Les séries ![]() ,
puisqu'on n'y trouve aucun terme étoilé, appartiennent à la
classe
,
puisqu'on n'y trouve aucun terme étoilé, appartiennent à la
classe ![]() . On peut ensuite passer de
. On peut ensuite passer de ![]() aux séries
aux séries ![]() et
et ![]() et de
et de ![]() aux séries
aux séries ![]() et
et ![]() ; donc les séries
; donc les séries ![]() et
et ![]() appartiennent aussi à la troisième classe. On déduit en effet de
la définition énoncée ci-dessus qu'on passe à série
horizontale
appartiennent aussi à la troisième classe. On déduit en effet de
la définition énoncée ci-dessus qu'on passe à série
horizontale ![]() depuis une autre
depuis une autre ![]() , s'il y a dans
, s'il y a dans ![]() un terme
souligné non étoilé et dans la même verticale un terme
étoilé appartenant à la série
un terme
souligné non étoilé et dans la même verticale un terme
étoilé appartenant à la série ![]() . Comme les
séries
. Comme les
séries ![]() appartiennent à la première, et les
séries
appartiennent à la première, et les
séries ![]() à la troisième, reste la série
à la troisième, reste la série ![]() qui
constitue la deuxième classe. Maintenant, dans chaque série
verticale dans laquelle se trouve un maximum étoilé appartenant
à une série de la première ou de la deuxième classe, on prend
un terme d'une série de la troisième classe
immédiatement inférieur et l'on note sous la série
verticale la différence des deux termes. De ces différences :
qui
constitue la deuxième classe. Maintenant, dans chaque série
verticale dans laquelle se trouve un maximum étoilé appartenant
à une série de la première ou de la deuxième classe, on prend
un terme d'une série de la troisième classe
immédiatement inférieur et l'on note sous la série
verticale la différence des deux termes. De ces différences :
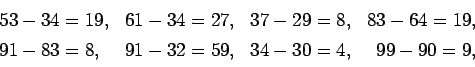
![\begin{displaymath}
\begin{array}{c}
(C) \\ [\medskipamount]
\begin{array}{r\ver...
... &\hfill 61 &\hfill 5 &\hfill &\hfill 5
\end{array}\end{array}\end{displaymath}](img71.png)
Nous voyons que dans le carré ![]() , on trouve sept maxima
transversaux et qu'un nouveau terme étoilé est apparu dans la
série
, on trouve sept maxima
transversaux et qu'un nouveau terme étoilé est apparu dans la
série ![]() ; cette série passe de la deuxième à la troisième
classe. J'écris en dessous les quantités dont les termes
étoilés des séries des premières et deuxièmes classes
dominent dans le carré
; cette série passe de la deuxième à la troisième
classe. J'écris en dessous les quantités dont les termes
étoilés des séries des premières et deuxièmes classes
dominent dans le carré ![]() les termes immédiatement inférieurs
de la troisième appartenant à la même verticale. Comme le
minimum de ces quantités est
les termes immédiatement inférieurs
de la troisième appartenant à la même verticale. Comme le
minimum de ces quantités est ![]() , en augmentant de
, en augmentant de ![]() toutes les
séries de la classe
toutes les
séries de la classe ![]() , je forme le carré
, je forme le carré
![\begin{displaymath}
\begin{array}{c}
(D) \\ [\medskipamount]
\begin{array}{r\ver...
... &\hfill 57 &\hfill 1 &\hfill &\hfill 1
\end{array}\end{array}\end{displaymath}](img75.png)
La disposition des astérisques doit, selon les règles données,
être un peu modifiée dans le carré ![]() ; ceci fait, les
séries
; ceci fait, les
séries ![]() et
et ![]() migrent respectivement des classes
migrent respectivement des classes ![]() et
et ![]() vers les classes
vers les classes ![]() et
et ![]() . Les termes étoilés
des classes
. Les termes étoilés
des classes ![]() et
et ![]() dominent les termes immédiatement
inférieurs de la classe
dominent les termes immédiatement
inférieurs de la classe ![]() et des mêmes verticales des
nombres
et des mêmes verticales des
nombres ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; en augmentant de leur minimum
; en augmentant de leur minimum ![]() toutes les séries de la classe
toutes les séries de la classe ![]() , je déduis le carré
, je déduis le carré
![\begin{displaymath}
\begin{array}{c}
(E) \\ [\medskipamount]
\begin{array}{r\ver...
...fill &\hfill 55 &\hfill &\hfill &\hfill
\end{array}\end{array}\end{displaymath}](img88.png)
La structure du carré ![]() ne diffère de celle du carré
ne diffère de celle du carré ![]() que par le fait que trois séries
que par le fait que trois séries ![]() et
et ![]() de la classe
de la classe ![]() sont passées à la classe
sont passées à la classe ![]() . En effet,
. En effet, ![]() et
et ![]() sont
passées à la classe
sont
passées à la classe ![]() parce que leurs termes étoilés
parce que leurs termes étoilés ![]() et
et ![]() sont devenus égaux aux termes des séries
sont devenus égaux aux termes des séries ![]() et
et ![]() placés dans les mêmes verticales ; quand à
placés dans les mêmes verticales ; quand à ![]() , elle est
passée à la classe
, elle est
passée à la classe ![]() car son terme étoilé est devenu
égal au terme dans la même verticale de la série
car son terme étoilé est devenu
égal au terme dans la même verticale de la série ![]() qui est
déjà passée à la classe
qui est
déjà passée à la classe ![]() . Du carré
. Du carré ![]() on déduit
par les règles énoncées le carré
on déduit
par les règles énoncées le carré
![\begin{displaymath}
\begin{array}{c}
(F) \\ [\medskipamount]
\begin{array}{r\ver...
...fill &\hfill 46 &\hfill &\hfill &\hfill
\end{array}\end{array}\end{displaymath}](img95.png)
Du carré ![]() , on déduit le carré
, on déduit le carré
![\begin{displaymath}
\begin{array}{c}
(G) \\ [\medskipamount]
\begin{array}{r\ver...
...fill &\hfill 45 &\hfill &\hfill &\hfill
\end{array}\end{array}\end{displaymath}](img100.png)
![\begin{displaymath}
\begin{array}{c}
(H) \\ [\medskipamount]
\begin{array}{r\ver...
...fill 40 &\hfill \underline{43}&\hfill 66
\end{array}\end{array}\end{displaymath}](img101.png)
La représentation symbolique du carré ![]() 7 apprend que
7 apprend que
Si le nombre de quantités dont sont formés les carrés est très grand, il ne sera pas difficile d'imaginer des artifices par lesquels on évitera la peine d'écrire ces nombres, puisque parmi leur grande masse, peu seulement sont nécessaires pour former un nouveau carré.
Soient de nouveaux ![]() des quantités positives ou nulles et,
ayant posé
des quantités positives ou nulles et,
ayant posé
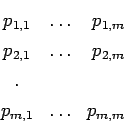

Grâce aux mêmes principes par lesquels on a obtenu un critère
pour que le problème soit résolu de la manière la plus simple,
c'est-à-dire par des quantités ![]() minimales, on obtient
aussi une méthode par laquelle la solution la plus simple peut
être déduite d'une solution quelconque. Posant
minimales, on obtient
aussi une méthode par laquelle la solution la plus simple peut
être déduite d'une solution quelconque. Posant
Si, en ajoutant des quantités quelconques
![]() aux séries horizontales du carré
aux séries horizontales du carré ![]() , on obtient un
carré possédant
, on obtient un
carré possédant ![]() maxima transversaux, la somme des termes qui
occupent dans le carré
maxima transversaux, la somme des termes qui
occupent dans le carré ![]() la même place que ces maxima
transversaux dans le carré dérivé, possédera une valeur
maximale parmi tous les agrégats de
la même place que ces maxima
transversaux dans le carré dérivé, possédera une valeur
maximale parmi tous les agrégats de ![]() termes transversaux du
carré
termes transversaux du
carré ![]() . D'où le problème d'inégalités
. D'où le problème d'inégalités
= 1 1cm
«trouver ![]() termes transversaux d'un carré donné
termes transversaux d'un carré donné ![]() formé
de
formé
de ![]() termes possédant une somme maximale, »
termes possédant une somme maximale, »
aura autant de solutions que l'on pourra trouver de systèmes de maxima transversaux dans le carré dérivé. On trouve tous ces systèmes si nous conservons seulement dans le carré dérivé les termes maximaux dans leur verticales, affectons à tous les autres une valeur nulle et formons enfin le déterminant de ces termes. En effet, les différents termes de ce déterminant fournissent les différentes solutions du problème. On peut démontrer réciproquement qu'une solution quelconque du problème d'inégalités précédent fournit un système de maxima transversaux du carré dérivé.
Dans notre exemple, il faut former le déterminant des termes
soulignés du carré ![]() , les autres termes de ce carré étant
affectés d'une valeur nulle. Ce déterminant peut être
successivement ramené aux déterminant plus simple formés des
quantités des carrés .
, les autres termes de ce carré étant
affectés d'une valeur nulle. Ce déterminant peut être
successivement ramené aux déterminant plus simple formés des
quantités des carrés .
 |
(2) |
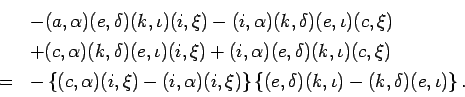
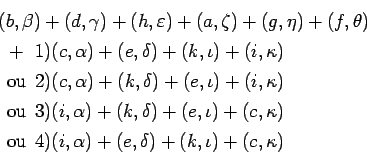
Ceux-ci s'expriment numériquement dans notre exemple par
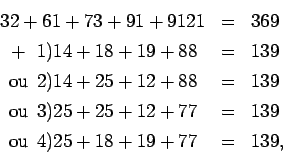
Réciproquement, si de quelque manière on connaît des termes
transversaux du carré proposé ![]() possédant une somme
maximale, on déduit par l'addition de quantités
minimales
possédant une somme
maximale, on déduit par l'addition de quantités
minimales ![]() aux séries horizontales du carré
proposé
aux séries horizontales du carré
proposé ![]() un carré dans lequel tous les maxima des
différentes séries verticales se trouvent aussi dans des séries
horizontales différentes.
un carré dans lequel tous les maxima des
différentes séries verticales se trouvent aussi dans des séries
horizontales différentes.
Je note bien entendu avec des astérisques ces termes transversaux
donnés possédant une somme minimale et j'ajoute aux séries
horizontales des quantités telles que leurs termes étoilés
deviennent égaux aux maxima de leurs séries verticales
respectives. J'écris chaque série augmentée sous les séries
restantes et je la compare aux séries restantes, aux précédentes
et aux suivantes. Pour ce faire, je désigne les séries
horizontales dénotées par les lettres ![]() , etc. par les
mêmes lettres une fois l'augmentation effectuée. Le tableau
suivant illustrera cette manière de faire sur notre exemple. On
suppose donnés les termes transversaux possédant une somme
maximale
, etc. par les
mêmes lettres une fois l'augmentation effectuée. Le tableau
suivant illustrera cette manière de faire sur notre exemple. On
suppose donnés les termes transversaux possédant une somme
maximale
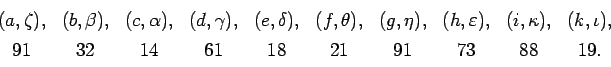
![\begin{displaymath}
\begin{array}{c}
(H) \\ [\medskipamount]
\begin{array}{r\ver...
...40 &\hfill 43\rlap{$^{\ast}$}&\hfill 66
\end{array}\end{array}\end{displaymath}](img139.png)
Dans la verticale ![]() , le terme étoilé est lui-même maximal,
donc au début la série horizontale
, le terme étoilé est lui-même maximal,
donc au début la série horizontale ![]() ne change pas ; dans la
verticale
ne change pas ; dans la
verticale ![]() , le maximum est
, le maximum est ![]() , donc l'horizontale
, donc l'horizontale ![]() doit
être écrite en dessous augmentée du nombre
doit
être écrite en dessous augmentée du nombre ![]() , ce qui forme la
ligne
, ce qui forme la
ligne ![]() . Revenus alors au premier terme, nous trouvons dans la
série
. Revenus alors au premier terme, nous trouvons dans la
série ![]() le maximum
le maximum ![]() , donc
, donc ![]() doit être augmentée
de
doit être augmentée
de ![]() , ce qui fournit la ligne
, ce qui fournit la ligne ![]() . Progressant jusqu'au
terme
. Progressant jusqu'au
terme ![]() , nous trouvons en
, nous trouvons en ![]() le maximum
le maximum ![]() placé
sur la ligne
placé
sur la ligne ![]() , donc
, donc ![]() doit être augmentée du nombre
doit être augmentée du nombre ![]() ,
ce qui fournit la ligne
,
ce qui fournit la ligne ![]() . De la même manière, les
séries
. De la même manière, les
séries ![]() et
et ![]() restent inchangées, j'augmente les
séries
restent inchangées, j'augmente les
séries ![]() des nombres
des nombres ![]() ce qui fournit les
lignes
ce qui fournit les
lignes
![]() . Alors, comme on trouve ligne
. Alors, comme on trouve ligne ![]() le terme
le terme ![]() de la verticale
de la verticale ![]() , plus grand que le terme
étoilé de la même verticale
, plus grand que le terme
étoilé de la même verticale ![]() placé ligne
placé ligne ![]() ,
j'ajoute
,
j'ajoute ![]() à la ligne
à la ligne ![]() , d'où l'on forme la ligne
, d'où l'on forme la ligne ![]() .
Dans
.
Dans ![]() et
et ![]() , le terme
, le terme ![]() de la verticale
de la verticale ![]() et plus
grand que le terme étoilé de cette même verticale, placé
en
et plus
grand que le terme étoilé de cette même verticale, placé
en ![]() , j'augmente donc la ligne
, j'augmente donc la ligne ![]() elle-même d'une unité,
ce qui fournit la ligne
elle-même d'une unité,
ce qui fournit la ligne ![]() . J'avance enfin jusqu'au
terme
. J'avance enfin jusqu'au
terme
![]() ; et comme le maximum de la verticale
; et comme le maximum de la verticale ![]() est
est ![]() , placé en
, placé en ![]() , je forme la ligne
, je forme la ligne ![]() en ajoutant
en ajoutant ![]() à la série
à la série ![]() . Ceci fait, le travail sera terminé. On a en
effet trouvé les séries
. Ceci fait, le travail sera terminé. On a en
effet trouvé les séries
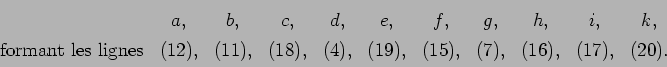
dont les termes étoilés sont maximaux dans leurs verticales, ce
qui était recherché. Nous voyons que ces séries constituent le
carré ![]() trouvé ci-dessus par une autre méthode.
trouvé ci-dessus par une autre méthode.
Au moyen de ce qui précède, on trouve une nouvelle solution du
problème proposé plus haut : si on connaît ![]() quantités
quelconques qui, ajoutées aux séries horizontales du carré
quantités
quelconques qui, ajoutées aux séries horizontales du carré ![]() ,
transforment ce carré en un autre dont les termes maximaux dans les
différentes verticales appartiennent à des séries horizontales
différentes, trouver les valeurs minimales de ces
,
transforment ce carré en un autre dont les termes maximaux dans les
différentes verticales appartiennent à des séries horizontales
différentes, trouver les valeurs minimales de ces ![]() quantités
positives ou nulles. Car, comme selon la proposition faite, on
connaît un carré dérivé de
quantités
positives ou nulles. Car, comme selon la proposition faite, on
connaît un carré dérivé de ![]() possédant
possédant ![]() maximaux
transversaux, on connaît aussi en
maximaux
transversaux, on connaît aussi en ![]()
![]() termes transversaux
possédant une somme maximale. Ceux-ci connus, selon la règle
donnée dans ce qui précède, on dérive facilement de
termes transversaux
possédant une somme maximale. Ceux-ci connus, selon la règle
donnée dans ce qui précède, on dérive facilement de ![]() , par
l'addition de quantités positives minimales, un carré
possédant
, par
l'addition de quantités positives minimales, un carré
possédant ![]() maxima transversaux. On voit en même temps comment,
connaissant un système de termes transversaux du carré
maxima transversaux. On voit en même temps comment,
connaissant un système de termes transversaux du carré ![]() possédant une somme maximale, on trouve facilement tous les autres
systèmes. Car, connaissant un tel système, nous voyons qu'il est
facile de déduire de
possédant une somme maximale, on trouve facilement tous les autres
systèmes. Car, connaissant un tel système, nous voyons qu'il est
facile de déduire de ![]() un carré possédant
un carré possédant ![]() maxima
transversaux ; dans celui-ci, si nous conservons seuls les maxima de
chaque verticale, évaluant les autres termes à
maxima
transversaux ; dans celui-ci, si nous conservons seuls les maxima de
chaque verticale, évaluant les autres termes à ![]() , chaque terme
non nul du déterminant du carré formé par ces quantités
fournit chaque système de maxima transversaux et donc chaque
système de termes transversaux du carré
, chaque terme
non nul du déterminant du carré formé par ces quantités
fournit chaque système de maxima transversaux et donc chaque
système de termes transversaux du carré ![]() possédant une
somme maximale ; en effet, les termes de chacun des systèmes occupent
les mêmes places dans les deux carrés.
possédant une
somme maximale ; en effet, les termes de chacun des systèmes occupent
les mêmes places dans les deux carrés.
Les équations différentielles proposées
Nous avons vu que la méthode par laquelle, en ajoutant des
quantités minimales positives aux séries horizontales, on déduit
un carré dans lequel tous les maxima des verticales se trouvent dans
les séries horizontales différentes peut être rendue plus facile
si l'on connaît de quelque façon un système de ![]() termes
transversaux du carré
termes
transversaux du carré ![]() possédant une somme maximale. Par
cette méthode plus facile, on trouve combien de fois chacune des
équations proposées doit être dérivée dans une réduction
la plus courte pour former les équations auxiliaires, à chaque
fois que l'on aura de quelque manière une forme normale quelconque
à laquelle les équations proposées se ramènent par une telle
réduction. Cette forme normale sera connue si les équations
différentielles proposées sont ainsi constituées que des
dérivées de variables différentes y atteignent l'ordre le plus
haut. Alors en effet, ces dérivées des différentes variables,
les plus hautes dans les différentes équations proposées, seront
aussi les plus hautes dans une forme normale, à laquelle les
équations différentielles proposées peuvent être ramenées
par une réduction la plus courte. Car les ordres de ces dérivées
constituent dans le carré
possédant une somme maximale. Par
cette méthode plus facile, on trouve combien de fois chacune des
équations proposées doit être dérivée dans une réduction
la plus courte pour former les équations auxiliaires, à chaque
fois que l'on aura de quelque manière une forme normale quelconque
à laquelle les équations proposées se ramènent par une telle
réduction. Cette forme normale sera connue si les équations
différentielles proposées sont ainsi constituées que des
dérivées de variables différentes y atteignent l'ordre le plus
haut. Alors en effet, ces dérivées des différentes variables,
les plus hautes dans les différentes équations proposées, seront
aussi les plus hautes dans une forme normale, à laquelle les
équations différentielles proposées peuvent être ramenées
par une réduction la plus courte. Car les ordres de ces dérivées
constituent dans le carré ![]() un système de
un système de ![]() termes
transversaux.
termes
transversaux.
Pour illustrer d'un exemple les recherches de ce paragraphe, supposons
données ![]() équations différentielles
équations différentielles
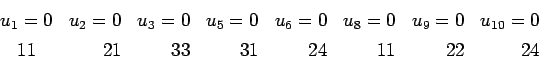
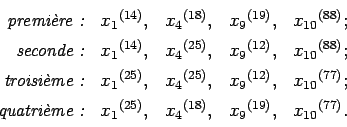
Nous considérons une réduction quelconque et,
dans le nombre total des équations différentielles auxiliaires et
proposées, nous en choisissons ![]() qui soient dérivées de chacune
des équations proposées par une différentiation la plus haute,
parmi lesquelles certaines peuvent être du nombre des équations
proposées si certaines de celles-ci ne sont absolument pas appelées
à former des équations auxiliaires par différentiation. Dans
chacune de ces
qui soient dérivées de chacune
des équations proposées par une différentiation la plus haute,
parmi lesquelles certaines peuvent être du nombre des équations
proposées si certaines de celles-ci ne sont absolument pas appelées
à former des équations auxiliaires par différentiation. Dans
chacune de ces ![]() équations, nous rassemblons les ordres des
dérivées les plus hautes de chaque variable et nous les disposons
en carré de la manière habituelle : dans un tel carré les maxima
des différentes séries verticales se trouvent nécessairement
aussi dans des séries horizontales différentes12. Et
d'après les règles énoncées ci-dessus, on peut se ramener d'un
tel carré à un autre, déduit de
équations, nous rassemblons les ordres des
dérivées les plus hautes de chaque variable et nous les disposons
en carré de la manière habituelle : dans un tel carré les maxima
des différentes séries verticales se trouvent nécessairement
aussi dans des séries horizontales différentes12. Et
d'après les règles énoncées ci-dessus, on peut se ramener d'un
tel carré à un autre, déduit de ![]() , en utilisant des nombres
positifs
, en utilisant des nombres
positifs ![]() minimaux. D'où l'on résume : d'une
réduction quelconque en forme normale des équations
différentielles proposées, on peut en déduire une la plus
brève.
minimaux. D'où l'on résume : d'une
réduction quelconque en forme normale des équations
différentielles proposées, on peut en déduire une la plus
brève.
Un système d'équations différentielles peut être ramené à
une unique équation différentielle en deux variables. Soient ces
deux variables : la variable indépendante ![]() et la variable
dépendante
et la variable
dépendante ![]() ; cette unique équations différentielle doit
être complétée par d'autres équations, par lesquelles on
exprime les variables dépendantes restantes en fonction de
; cette unique équations différentielle doit
être complétée par d'autres équations, par lesquelles on
exprime les variables dépendantes restantes en fonction de ![]() ,
de
,
de ![]() et des dérivées de
et des dérivées de ![]() , ces dérivées ne montant
pas jusqu'à l'ordre de l'équation différentielle ayant lieu
entre
, ces dérivées ne montant
pas jusqu'à l'ordre de l'équation différentielle ayant lieu
entre ![]() et
et ![]() . Comme il est habituel que ce type de forme
normale soit considéré avant d'autres par les analystes,
j'indiquerai combien de fois successives chacune des équations
différentielles proposées
. Comme il est habituel que ce type de forme
normale soit considéré avant d'autres par les analystes,
j'indiquerai combien de fois successives chacune des équations
différentielles proposées
![]() doivent être dérivées pour faire apparaître les équations
différentielles nécessaires à cette réduction.
doivent être dérivées pour faire apparaître les équations
différentielles nécessaires à cette réduction.
Nous supposons que les équations différentielles
proposées
![]() doivent être
dérivées
doivent être
dérivées
![]() fois pour fournir les
équations auxiliaires nécessaires à une réduction la plus
courte. J'ai enseigné ci-dessus comment l'on trouve ces
nombres
fois pour fournir les
équations auxiliaires nécessaires à une réduction la plus
courte. J'ai enseigné ci-dessus comment l'on trouve ces
nombres
![]() . En ajoutant les
nombres
. En ajoutant les
nombres
![]() aux séries horizontales du
carré
aux séries horizontales du
carré ![]() , je forme un autre carré
, je forme un autre carré ![]() , dans lequel je
distingue d'un astérisque un système complet de maxima
transversaux et je souligne les maxima restant des différentes
verticales. Si toutes les variables sont à éliminer, sauf la
variable indépendante
, dans lequel je
distingue d'un astérisque un système complet de maxima
transversaux et je souligne les maxima restant des différentes
verticales. Si toutes les variables sont à éliminer, sauf la
variable indépendante ![]() et la variable dépendante
et la variable dépendante ![]() ,
je cherche le terme étoilé de la
,
je cherche le terme étoilé de la ![]()
![]() verticale, qui est dans la
verticale, qui est dans la ![]()
![]() série horizontale ; dans
la
série horizontale ; dans
la ![]()
![]() série horizontale, je cherche les termes soulignés,
dans chacune de leurs verticales chacun des termes étoilés, dans
les séries horizontales de ceux-ci de nouveaux les termes
soulignés, dans leurs verticales de nouveau les termes étoilés,
et ainsi de suite. Dans cette circonstance, il n'est pas nécessaire
de revenir davantage aux termes étoilés déjà observés.
Continuant cette tâche, autant que faire se peut, je dirai que
toutes les séries horizontales auxquelles on parvient part ce
procédé sont attachées à la
série horizontale, je cherche les termes soulignés,
dans chacune de leurs verticales chacun des termes étoilés, dans
les séries horizontales de ceux-ci de nouveaux les termes
soulignés, dans leurs verticales de nouveau les termes étoilés,
et ainsi de suite. Dans cette circonstance, il n'est pas nécessaire
de revenir davantage aux termes étoilés déjà observés.
Continuant cette tâche, autant que faire se peut, je dirai que
toutes les séries horizontales auxquelles on parvient part ce
procédé sont attachées à la ![]()
![]() d'où nous avons
commencé. J'augmente ces séries ainsi que la
d'où nous avons
commencé. J'augmente ces séries ainsi que la ![]()
![]() d'une
même quantité, la plus petite telle que l'un de leurs termes qui
ne soit ni étoilés ni souligné devienne égal à un terme
étoilé de sa verticale. La série horizontale de ce terme
s'ajoutant aux séries attachées à la
d'une
même quantité, la plus petite telle que l'un de leurs termes qui
ne soit ni étoilés ni souligné devienne égal à un terme
étoilé de sa verticale. La série horizontale de ce terme
s'ajoutant aux séries attachées à la ![]()
![]() série,
j'augmente de nouveau la
série,
j'augmente de nouveau la ![]()
![]() série et celles lui étant
attachées, dont le nombre vient d'être accru, de la plus petite
quantité telle que l'un de leurs termes n'étant ni étoilé ni
souligné ne devienne égal à un terme étoilé de sa
verticale ; ceci fait, le nombre des séries attachées à
la
série et celles lui étant
attachées, dont le nombre vient d'être accru, de la plus petite
quantité telle que l'un de leurs termes n'étant ni étoilé ni
souligné ne devienne égal à un terme étoilé de sa
verticale ; ceci fait, le nombre des séries attachées à
la ![]()
![]() augmente de nouveau ; et ainsi j'augmente de plus en plus
le nombre de ces séries, jusqu'à ce qu'on parvienne à un
carré
augmente de nouveau ; et ainsi j'augmente de plus en plus
le nombre de ces séries, jusqu'à ce qu'on parvienne à un
carré
![]() , dont toutes les séries horizontales
sont attachées à la
, dont toutes les séries horizontales
sont attachées à la ![]()
![]() . Je déduis alors
de
. Je déduis alors
de
![]() un carré
un carré
![]() en
augmentant les séries horizontales d'une même quantité, telle
que le terme de la
en
augmentant les séries horizontales d'une même quantité, telle
que le terme de la ![]()
![]() série horizontale, appartenant à
la
série horizontale, appartenant à
la ![]()
![]() verticale soit rendu égal à la plus grande somme que puisse revêtir un système de
verticale soit rendu égal à la plus grande somme que puisse revêtir un système de ![]() termes transversaux du carré
termes transversaux du carré ![]() 13. Les nombres dont les
séries horizontales du carré
13. Les nombres dont les
séries horizontales du carré ![]() doivent être augmentées
pour produire le carré
doivent être augmentées
pour produire le carré
![]() indiquent combien
de fois chacune des équations différentielles proposées doit
être dérivée afin de découvrir les équations auxiliaires
nécessaires pour qu'apparaissent, par de simples éliminations, une
équation différentielle entre les seules variables
indiquent combien
de fois chacune des équations différentielles proposées doit
être dérivée afin de découvrir les équations auxiliaires
nécessaires pour qu'apparaissent, par de simples éliminations, une
équation différentielle entre les seules variables ![]() et
et ![]() et les autres équations par lesquelles les variables
restantes sont exprimées en fonction de
et les autres équations par lesquelles les variables
restantes sont exprimées en fonction de
![]() et des
dérivées de
et des
dérivées de ![]() .
.
Le carré ![]() est le même que j'ai désigné ci-dessus
par
est le même que j'ai désigné ci-dessus
par ![]() dans notre exemple. Nous supposons que la
dans notre exemple. Nous supposons que la ![]()
![]() verticale
est la série
verticale
est la série ![]() , dont le terme étoilé
, dont le terme étoilé ![]() appartient à
la série horizontale
appartient à
la série horizontale ![]() , dans laquelle se trouve les termes
soulignés
, dans laquelle se trouve les termes
soulignés ![]() appartenant aux
verticales
appartenant aux
verticales
![]() dont les termes étoilés
appartiennent aux séries
dont les termes étoilés
appartiennent aux séries ![]() dans lesquelles on a les termes
soulignés
dans lesquelles on a les termes
soulignés ![]() et
et ![]() , appartenant aux verticales
, appartenant aux verticales ![]() et
et ![]() , les termes étoilés appartiennent aux séries
, les termes étoilés appartiennent aux séries ![]() et
et ![]() , dans cette dernière, on a le terme souligné
, dans cette dernière, on a le terme souligné ![]() ,
appartenant à la verticale
,
appartenant à la verticale ![]() dont le terme étoilé se trouve
en
dont le terme étoilé se trouve
en ![]() , laquelle série contient l'unique terme souligné
, laquelle série contient l'unique terme souligné ![]() , dont
la verticale a déjà servi. De là, on trouve les séries
attachées à
, dont
la verticale a déjà servi. De là, on trouve les séries
attachées à ![]() :
: ![]() . En augmentant toutes les
séries
. En augmentant toutes les
séries
![]() d'une unité,
d'une unité, ![]() s'ajoute aux séries
attachées à
s'ajoute aux séries
attachées à ![]() , car avec cet incrément, le terme
, car avec cet incrément, le terme ![]() des
séries
des
séries ![]() ou
ou ![]() , appartenant à la verticale
, appartenant à la verticale ![]() devient
devient ![]() , lequel nombre est égal au terme étoilé de la
verticale
, lequel nombre est égal au terme étoilé de la
verticale ![]() qui appartient à l'horizontale
qui appartient à l'horizontale ![]() . J'augmente de
nouveau les séries
. J'augmente de
nouveau les séries
![]() du nombre
du nombre ![]() , ceci fait,
, ceci fait, ![]() s'ajoute aux séries attachées à
s'ajoute aux séries attachées à ![]() ; enfin j'augmente du
nombre
; enfin j'augmente du
nombre ![]() toutes les séries sauf
toutes les séries sauf ![]() , afin que
, afin que ![]() lui-même
rejoigne les séries attachées à
lui-même
rejoigne les séries attachées à ![]() . D'où le
carré
. D'où le
carré
![]() est constitué à partir des séries
de
est constitué à partir des séries
de ![]() ou
ou ![]() :
:

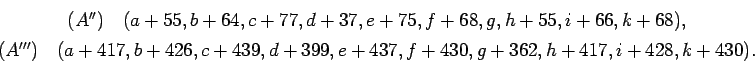
Par la même méthode, nous obtenons le
carré
![]() dans lesquels toutes les séries
horizontales sont attachées à l'une des séries
dans lesquels toutes les séries
horizontales sont attachées à l'une des séries
![]() en ajoutant aux séries du carrés
en ajoutant aux séries du carrés ![]()
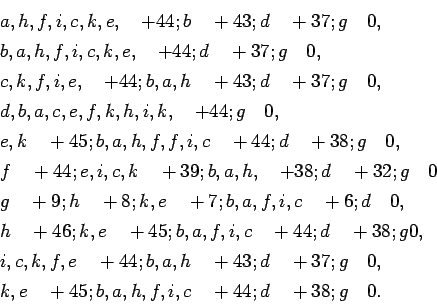
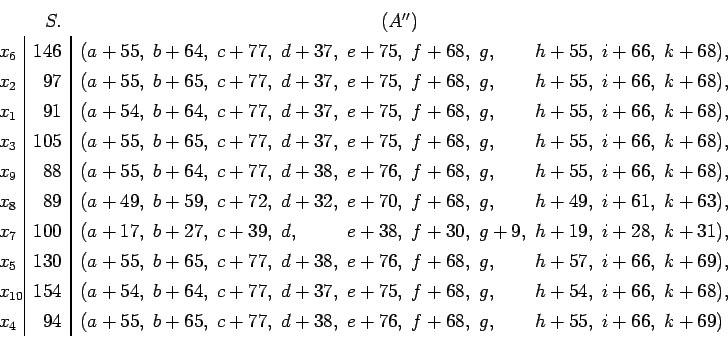
Dans les séries horizontales, première, deuxième, ..., dixième du
carré ![]() ou
ou ![]() , on a les termes étoilés
, on a les termes étoilés

En ajoutant à ces termes

Dans un carré
![]() , soit
, soit ![]() le terme étoilé de
la série horizontale à laquelle les séries restantes sont
attachés : on pourra parvenir de
le terme étoilé de
la série horizontale à laquelle les séries restantes sont
attachés : on pourra parvenir de ![]() à un quelconque autre terme
étoilé par un cheminement continu de la même série horizontale
et d'un terme souligné à un terme étoilé de la même
verticale. Nous présentons, par exemple, le premier carré obtenu
ci-dessus
à un quelconque autre terme
étoilé par un cheminement continu de la même série horizontale
et d'un terme souligné à un terme étoilé de la même
verticale. Nous présentons, par exemple, le premier carré obtenu
ci-dessus
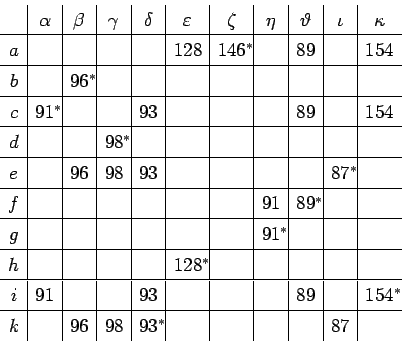
dans lequel je n'ai mis que les termes étoilés et soulignés
ou égaux au termes étoilés de la même verticale (en omettant
de souligner). Dans
ce carré, toutes les séries horizontales dépendent de ![]() dont
le terme étoilé est
dont
le terme étoilé est ![]() . De celui-ci, on arrive ainsi aux
autres termes étoilés :
. De celui-ci, on arrive ainsi aux
autres termes étoilés :
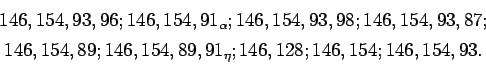
Si l'on supprime du carré proposé
![]() la série
verticale du terme
la série
verticale du terme ![]() , à partir duquel nous avons commencé et une
autre horizontale quelconque, on déterminera facilement dans le
carré restant un système de maxima transversaux. Nous désignons
par
, à partir duquel nous avons commencé et une
autre horizontale quelconque, on déterminera facilement dans le
carré restant un système de maxima transversaux. Nous désignons
par
![]() le terme égal à
le terme égal à ![]() dans la série horizontale
de
dans la série horizontale
de ![]() et placé dans la verticale de
et placé dans la verticale de ![]() et nous supposons que le
terme étoilé de la série horizontale supprimée est
et nous supposons que le
terme étoilé de la série horizontale supprimée est ![]() ;
puisque, selon la loi fixée, l'on passe de
;
puisque, selon la loi fixée, l'on passe de ![]() à
à ![]() par les
termes étoilés intermédiaires
par les
termes étoilés intermédiaires
![]() . Ceci posé, les termes étoilés restant du
carré proposé seront eux-mêmes des maxima transversaux du
carré restant ; mais au lieu de
. Ceci posé, les termes étoilés restant du
carré proposé seront eux-mêmes des maxima transversaux du
carré restant ; mais au lieu de
![]() , il faut prendre les termes
, il faut prendre les termes
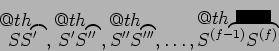
Nous considérons un carré quelconque
![]() dans lequel le terme étoilé d'une série horizontale à laquelle
toutes les autres sont attachées appartient à
la
dans lequel le terme étoilé d'une série horizontale à laquelle
toutes les autres sont attachées appartient à
la ![]()
![]() verticale, lequel terme je
désignerai par
verticale, lequel terme je
désignerai par ![]() . Ce
carré
. Ce
carré
![]() est celui-là même, que l'on
doit former à chaque fois que l'on se propose d'éliminer toutes
les variables sauf
est celui-là même, que l'on
doit former à chaque fois que l'on se propose d'éliminer toutes
les variables sauf ![]() et
et ![]() . Nous supposons ensuite que le
carré
. Nous supposons ensuite que le
carré
![]() provient de l'addition aux
séries horizontales du carré
provient de l'addition aux
séries horizontales du carré ![]() des quantités
des quantités
=
by -0.7cm
= 1 0.7cm
Soient entre la variable indépendante ![]() et les
et les ![]() variables
dépendantes
variables
dépendantes
![]() , les équations
différentielles
, les équations
différentielles
= 1 0.7cm
On forme un carré contenant ![]() séries verticales et autant de séries
horizontales; dans la
séries verticales et autant de séries
horizontales; dans la ![]()
![]() verticale
et la
verticale
et la ![]()
![]() horizontale, on place l'ordre de la plus haute
dérivée de la variable
horizontale, on place l'ordre de la plus haute
dérivée de la variable ![]() qui intervient dans
l'équation
qui intervient dans
l'équation ![]() . Ayant supprimé la
. Ayant supprimé la ![]()
![]() série
horizontale et la
série
horizontale et la ![]()
![]() série verticale de ce carré, on
cherche la somme maximale
série verticale de ce carré, on
cherche la somme maximale
![]() que puisse atteindre
que puisse atteindre ![]() de ses termes tous placés dans des séries horizontales
différentes et dans des verticales différentes : pour former le
système d'équations auxiliaires au moyen duquel apparaît
l'équation différentielle entre
de ses termes tous placés dans des séries horizontales
différentes et dans des verticales différentes : pour former le
système d'équations auxiliaires au moyen duquel apparaît
l'équation différentielle entre ![]() et
et ![]() ,
l'équation
,
l'équation ![]() doit être dérivée
doit être dérivée
![]() fois.
Le nombre cherché
fois.
Le nombre cherché
![]() sera aussi égal à l'ordre des
équations différentielles qui apparaissent si nous enlevons des
équations considérées
sera aussi égal à l'ordre des
équations différentielles qui apparaissent si nous enlevons des
équations considérées ![]() et remplaçons
et remplaçons ![]() par
une constante15.
par
une constante15.
Les nombres
![]() sont fournis par le carré
sont fournis par le carré
![]() , dont j'ai
expliqué comment on le déduit du carré
, dont j'ai
expliqué comment on le déduit du carré ![]() . J'ai
donné ci-dessus les valeurs des nombres
. J'ai
donné ci-dessus les valeurs des nombres ![]() et
et
![]() correspondant à l'exemple proposé ; on résout par ces nombres cent
problèmes d'inéquation, à savoir en supprimant en même temps du
carré proposé une série verticale et une série horizontales
quelconques, trouver dans les cent carrés résultants la somme
maximale des termes transversaux. On trouvera facilement dans chacun
de ces carrés des termes transversaux possédant la somme maximale
si l'on reprend ce que j'ai expliqué ci-dessus à propos de la
manière d'aller d'un terme
correspondant à l'exemple proposé ; on résout par ces nombres cent
problèmes d'inéquation, à savoir en supprimant en même temps du
carré proposé une série verticale et une série horizontales
quelconques, trouver dans les cent carrés résultants la somme
maximale des termes transversaux. On trouvera facilement dans chacun
de ces carrés des termes transversaux possédant la somme maximale
si l'on reprend ce que j'ai expliqué ci-dessus à propos de la
manière d'aller d'un terme ![]() du carré
du carré
![]() à
un autre terme étoilé quelconque
à
un autre terme étoilé quelconque ![]() par des termes
étoilés intermédiaires.
par des termes
étoilés intermédiaires.
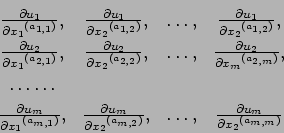
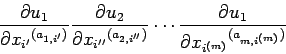
Si ![]() ne s'annule pas, l'ordre du système atteindra toujours
la valeur
ne s'annule pas, l'ordre du système atteindra toujours
la valeur ![]() assignée par la théorie générale que j'ai
exposée. J'appelle la quantité
assignée par la théorie générale que j'ai
exposée. J'appelle la quantité ![]() le déterminant du
système d'équations différentielles considéré.
le déterminant du
système d'équations différentielles considéré.
Dans notre exemple, il se fait que
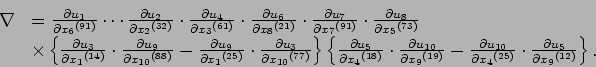

to to 4cm