jMEF.UnivariateGaussian Class Reference
Public Member Functions | |
| double | F (PVector T) |
Computes the log normalizer 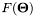 . . | |
| PVector | gradF (PVector T) |
Computes 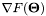 . . | |
| double | G (PVector H) |
Computes 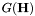 . . | |
| PVector | gradG (PVector H) |
Computes 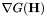 . . | |
| PVector | t (PVector x) |
Computes the sufficient statistic 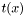 . . | |
| double | k (PVector x) |
Computes the carrier measure 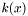 . . | |
| PVector | Lambda2Theta (PVector L) |
| Converts source parameters to natural parameters. | |
| PVector | Theta2Lambda (PVector T) |
| Converts natural parameters to source parameters. | |
| PVector | Lambda2Eta (PVector L) |
| Converts source parameters to expectation parameters. | |
| PVector | Eta2Lambda (PVector H) |
| Converts expectation parameters to source parameters. | |
| double | density (PVector x, PVector param) |
Computes the density value 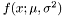 . . | |
| PVector | drawRandomPoint (PVector L) |
| Draws a point from the considered distribution. | |
| double | KLD (PVector LP, PVector LQ) |
| Computes the Kullback-Leibler divergence between two univariate Gaussian distributions. | |
Static Public Member Functions | |
| static double | Rand (double mu, double sigma) |
| Box-Muller transform/generator. | |
| static double | Rand () |
| Box-Muller transform/generator. | |
Detailed Description
- Version:
- 1.0
License
See file LICENSE.txtDescription
The univariate Gaussian distribution is an exponential family and, as a consequence, the probability density function is given by
![\[ f(x; \mathbf{\Theta}) = \exp \left( \langle t(x), \mathbf{\Theta} \rangle - F(\mathbf{\Theta}) + k(x) \right) \]](form_0.png)
where 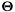 are the natural parameters. This class implements the different functions allowing to express a univariate Gaussian distribution as a member of an exponential family.
are the natural parameters. This class implements the different functions allowing to express a univariate Gaussian distribution as a member of an exponential family.
Parameters
The parameters of a given distribution are:- Source parameters
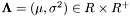
- Natural parameters
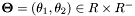
- Expectation parameters

Member Function Documentation
Computes the density value 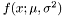 .
.
- Parameters:
-
x point param parameters (source, natural, or expectation)
- Returns:
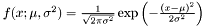
Draws a point from the considered distribution.
- Parameters:
-
L source parameters 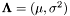
- Returns:
- a point
Converts expectation parameters to source parameters.
- Parameters:
-
H natural parameters 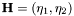
- Returns:
- source parameters
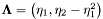
| double jMEF.UnivariateGaussian.F | ( | PVector | T | ) |
Computes the log normalizer 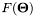 .
.
- Parameters:
-
T parameters 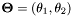
- Returns:
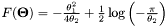
| double jMEF.UnivariateGaussian.G | ( | PVector | H | ) |
Computes 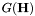 .
.
- Parameters:
-
H expectation parameters 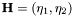
- Returns:
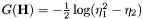
Computes 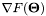 .
.
- Parameters:
-
T natural parameters 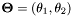
- Returns:
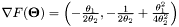
Computes 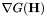 .
.
- Parameters:
-
H expectation parameters 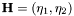
- Returns:
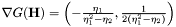
| double jMEF.UnivariateGaussian.k | ( | PVector | x | ) |
Computes the carrier measure 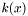 .
.
- Parameters:
-
x a point
- Returns:
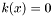
Computes the Kullback-Leibler divergence between two univariate Gaussian distributions.
- Parameters:
-
LP source parameters 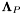
LQ source parameters 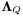
- Returns:
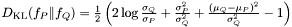
Converts source parameters to expectation parameters.
- Parameters:
-
L source parameters 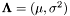
- Returns:
- expectation parameters
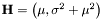
Converts source parameters to natural parameters.
- Parameters:
-
L source parameters 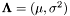
- Returns:
- natural parameters
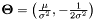
| static double jMEF.UnivariateGaussian.Rand | ( | ) | [static] |
Box-Muller transform/generator.
- Returns:
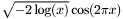 where
where 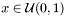
| static double jMEF.UnivariateGaussian.Rand | ( | double | mu, | |
| double | sigma | |||
| ) | [static] |
Box-Muller transform/generator.
- Parameters:
-
mu mean 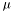
sigma variance 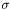
- Returns:
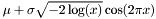 where
where 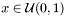
Computes the sufficient statistic 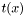 .
.
- Parameters:
-
x a point
- Returns:
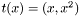
Converts natural parameters to source parameters.
- Parameters:
-
T natural parameters 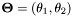
- Returns:
- source parameters
The documentation for this class was generated from the following file:
 1.5.9
1.5.9