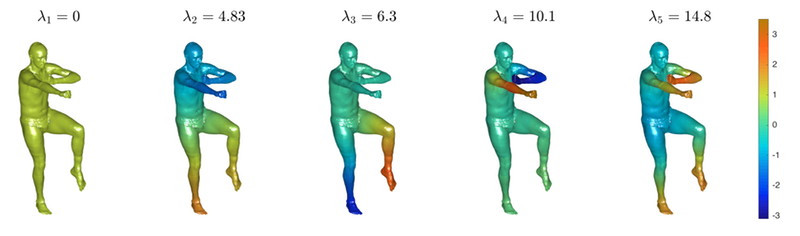|
Course Notes:
You can find a set of course notes prepared for this
course here:
Computing and
Processing Correspondences with Functional Maps (62 pages, 6.3MB), or a compressed version (1.8MB).
Demo Code:
-
The following code demonstrates the computation of the Laplacian eigenbasis on a triangle
mesh using cotangent weights: laplacian_basis_demo.zip.
To try it, simply run cot_laplace_demo.m in MATLAB. This should
produce an image showing the first 5 eigenfunctions of the Laplace-Beltrami operator and
their associated eigenvalues. You should get an image that looks like this:
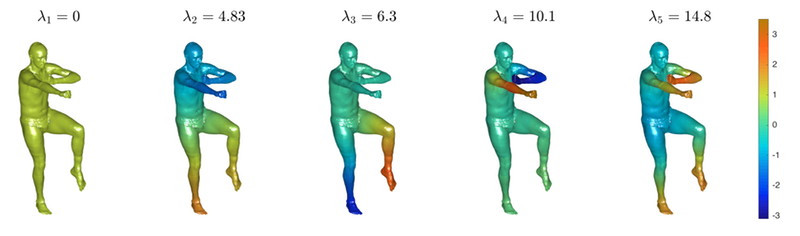
-
The following code shows how to convert a point-to-point map to its functional
representation, and provides a basic method for converting it back and computing the resulting
error: fmap_reconstruction_demo.zip. To
try it, first run fmap_computation_demo.m in MATLAB. This should
create an image showing the functional map matrix corresponding to a functional map between
two shapes. This image should look like this. You can
also run fmap_reconstruction_demo.m in MATLAB, which will
convert a functional map to a point-to-point one using the basic approach described in the
2012 article and then compute the reconstruction error. This should produce the following plot.
Functional Map Computation Code:
-
The following code implements a method for computing
functional maps described in the paper:
Informative Descriptor Preservation via Commutativity
for Shape Matching, Eurographics 2017.
You can find this code here.
Please see the included README file for an example use of the code.
-
The following set of MATLAB scripts implements the basic
pipeline for computing a map between a pair of shapes using the
functional representation. It is based on the description given in
the following paper and was used to obtain the results presented
in this paper:
Functional Maps: A Flexible Representation of Maps Between
Shapes, SIGGRAPH 2012.
You can find this code here.
To use it, please run the file runme.m inside "clean_code" to see an example
with two shapes (cat0 and cat10). Note that this code requires as
input some shape segmentations (provided for these examples) and tries
to establish correspondences between segments, which are used as input
constraints to find the functional map. The segmentations used to obtain results
shown in the paper can be found here. In addition,
you can find the code for computing persistence-based segmentations (used to generate these results):
here.
-
The following code (also in MATLAB) implements the method described in the paper:
Non-rigid Puzzles, SGP 2016.
You can find this code here.
In particular, you can reproduce the figures presented in the paper by running the script
reproduce_paper_figures.m To run it on your own data,
run the function solveNonRigidPuzzle
with the parameters used for Figure 1 (in the reproduce_paper_figures.m script).
-
The following code implements the method described in the paper:
Point-wise Map Recovery and Refinement from Functional Correspondence, VMV 2015.
You can find this code here.
To use it simply run
demo.m which loads two example shapes. To use it on your own data, simply
replace the shapes with your own (the only requirement is to have pre-computed eigenvectors of the Laplacian
of each shape). See run_cpd.m for the format.
-
The following code implements the method described in the paper:
Supervised Descriptor Learning for Non-Rigid Shape Matching,
NORDIA 2014.
You can find this code here
To use it please look at the the Readme.txt,
which describes how to reproduce Figure 5b of the paper. You need to download the TOSCA dataset
which can be found here.
Further Reading:
Below is a non-exhaustive list of articles covered in the course and
some follow-up works based on the functional map representation.
- Functional Maps: A Flexible Representation of Maps Between
Shapes, M. Ovsjanikov et al., SIGGRAPH 2012.
- Coupled quasi-harmonic bases, A. Kovnatsky et al., Computer
Graphics Forum 2012.
- Sparse modeling of intrinsic correspondences., J. Porkass et
al., Computer Graphics Forum, 2013.
- Analysis and Visualization of Maps Between Shapes,
M. Ovsjanikov et al., Computer Graphics Forum 2013.
- Map-Based Exploration of Intrinsic Shape Differences and
Variability, R. Rustamov et al., SIGGRAPH 2013.
- An Operator Approach to Tangent Vector Field
Processing, O. Azencot et al., Computer Graphics Forum 2013.
- Shape Matching via Quotient Spaces, M. Ovsjanikov et al., Computer Graphics Forum 2013.
- Supervised Descriptor Learning for Non-Rigid Shape Matching,
E. Corman et al., Proc. NORDIA 2014.
- Functional map networks for analyzing and exploring large shape
collections, Q. Huang et al., SIGGRAPH 2014.
- Shape-from-operator: Recovering shapes from intrinsic
operators, D. Boscaini et al., Computer Graphics Forum, 2015.
- Continuous Matching via Vector Field Flow, E. Corman et al.,
Computer Graphics Forum 2015.
- Point-wise map recovery and refinement from functional
correspondence, E. Rodolà et al., Computer Graphics Forum 2016.
- Partial functional correspondence, E. Rodolà et al., Computer
Graphics Forum 2016.
- Non-rigid puzzles, O. Litany et al., Computer Graphics Forum 2016.
- Regularized point-wise map recovery from functional
correspondence, E. Rodolà et al., Computer Graphics Forum 2016.
- Informative descriptor preservation via commutativity for shape matching,
D. Nogneng, M. Ovsjanikov, Eurographics 2017.
|
|