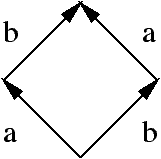
Figure 5: Interleaving semantics of a | b




Figure 5: Interleaving semantics of a | b
This fact creates problems in particular in static analysis of (asynchronous) concurrent systems in that interleaving builds a lot of uninteresting states in the modelisation, hence inducing a high cost in verification. This is called the state-space explosion problem. Some techniques exist now to circumvent part of the problem, actually mostly derived from truly-concurrent considerations (originally Petri nets in [Valmari, 1990] and Mazurkiewicz trace theory in [Godefroid and Wolper, 1991]). Another problem is that refinement, which is a very convenient technique in program analysis, is very difficult to apply in interleaving semantics, see [van Glabbeek and Goltz, 1989] for instance: suppose that action a is in fact non-atomic and is composed of two subactions c then d, then a | b in interleaving semantics is no longer equivalent to a then b or b then a. The path c then b then d is missing there (see Figure 6, the missing part is represented by the dashed line). This implies that interleaving semantics is bound to describe all atomic actions for the derived analyses to be correct, hence incurring a great complexity.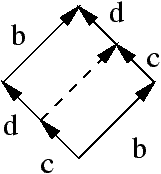
Figure 6: A refinement of a | b


