Identification avec retard

On considère maintenant un système à retard écrit sous la forme $\sum_{i=0}^{n} a_{i}x^{(i)}(t) + b u(t-h)$, avec $a_{n}=-1$. Soit $f$ une fonction telle que $f^{(j)}(0)=f^{(j)}(1)=0$, pour $j<m$ avec $m\ge n$. On pose $I_{x,f,T_{1},T_{2}}=\int_{T_{1}}^{T_{2}}f((\tau-T_{1})/(T_{2}-T_{1})) x(\tau)d\tau$. En intégrant par parties, on déduit de l'équation du système

$$\sum_{i=0}^{n} (T_{1}-T_{2})^{-i}a_{i}I_{x,f^{(i)},T_{1},T_{... ...^{(\ell)},T_{1},T_{2}}h^{\ell}\right) + O(h^{\min(k+1,m)}) =0.$$

On désignera par $E_{(T_{1},T_{2}),x,u}$ cette équation, où le terme $O(h^{\min(k+1,m)})$ a été négligé et chaque puissance $h^{\ell}$ remplacée par $b_{\ell}/b$ afin de se ramener à une équation linéaire. Pour $x$ et $u$ génériques, on résoud par moindres carrés le système $E_{s,y,u}$, $s\in S$ en les inconnues $a_{i}$ et $b_{\ell}$, où $S$ est un ensemble générique d'intervalles d'un cardinal suffisant. On obtient des approximations ${\widehat{a}}_{i}$ et ${\widehat{b}}_{0}$ des coefficients $a_{i}$ et $b$ et une approximation du retard égale à ${\widehat{b}}_{1}/{\widehat{b}}_{0}$. La précision du résultat sera d'autant meilleure que le rapport $h/(T_{2}-T_{1})$ est petit pour chaque couple de $S$.

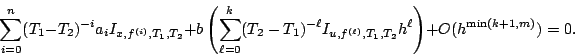
Une fois obtenue une approximation $h_{0}$ du retard, on améliore la précision du résultat en résolvant le système $E_{s,y,u_{h_{0}}}$, $s\in S$, où $u_{h_{0}}(t)=u(t-h_{0})$, ce qui donnera la nouvelle approximation $h_{0}+{\widehat{b}}_{1}/{\widehat{b}}_{0}$. On itère le processus.

Pour de meilleurs résultats, on peut également choisir une fonction $f$ telle que $f(t+h)=\sum_{k=0}^{p} a_{k}(h) f^{(k)}$, par exemple $f(t)=t^{m}(1-t)^{m}$ ou $\sin^{m}(\pi t)$.

Exemple 2   Nous avons fait des simulations numériques avec $f(t)=\sin^{2}(t)$ pour un système d'ordre $2$. L'équation $E_{(T_{1},T_{2}),y,u}$ s'écrit alors $(T_{1}-T_{2})^{-1}a_{1}I_{x,f',T_{1},T_{2}}$ $+a_{0}I_{x,f,T_{1},T_{2}}+b_{0}I_{u,f,T_{1},T_{2}}$ $-b_{1}I_{u,cos(2t),T_{1},T_{2}}$ $+b_{2}I_{u,sin(2t),T_{1},T_{2}}+0(h^{2})$ $=(T_{1}-T_{2})^{-2}I_{x,f'',T_{1},T_{2}}$ et l'on obtient une approximation de $h$ égale à $h_{0}+{\rm acos}({\widehat{b}}_{2}/{\widehat{b}}_{0})$ à partir d'un système $E_{s,u_{h_{0}}}$, $s\in S$, où $h_{0}$ est une estimation préalable du retard.

Les valeurs des coefficients sont les mêmes que celles de l'exemple $1$. On a choisi la commande $u=60\cos(1,23t+0,33*\sin(t)-0,47\cos(0,5t))$ et un retard $h=4$. Le bruit est un bruit gaussien et la fréquence d'échantillonnage est de $500$ Hz. On a pris pour $S$ les couples $(10k,10k+15)$, $1\le k\le 9$. On part de $h_{0}=0$ et l'on itère les calculs une cinquantaine de fois (en un temps de l'ordre de quelques secondes sur un Dell Latitude D400), ce qui est suffisant pour atteindre un point fixe à la précision numérique près.

Le tableau ci-dessous, qui donne la moyenne (M.) et l'écart type (É.) de séries de cent estimations des coefficients et du retard réalisées pour des bruits gaussiens d'écarts types croissant, montre que l'on obtient des estimations crédibles, même pour un niveau de bruit notable.

É. du bruit	M. $a_{1}$	É. $a_{1}$	M. $a_{0}$	É. $a_{0}$	M. $b$	É. $b$	M. $h$	É. $h$
1	-1,2013301	0,0200702	-0,3503987	0,0070836	2,0022146	0,0420976	4,0008356	0,0153991
2	-1,2012952	0,0280813	-0,3504493	0,0101866	2,0023815	0,059994	4,000781	0,0234536
5	-1.1763456	0.0848359	-0.3414087	0.0298163	1.9487169	0.1772991	3.9744399	0.0659957
10	-1.1252249	0.1591226	-0.3234272	0.0559417	1.8422743	0.3327821	3.9187225	0.1328752

Tableau 1.