Time delay systems are known to take an important place in many fields of application. We refer to [7] and the references therein for more details on the subject. We propose a method for parameters and delay identification, inspired by the work of Fliess and Sira-Ramìrez [3].
We write the system
![]() , with
, with
![]() . The output is
. The output is ![]() where
where ![]() stands for the noise
which is such that
stands for the noise
which is such that
![]() goes to
goes to ![]() when
when ![]() goes
to infinity. The main idea is to use a family of functions
goes
to infinity. The main idea is to use a family of functions ![]() such that
such that
![]() for
for ![]() . Let
. Let
![]() . Integrating by
parts, we get
. Integrating by
parts, we get
![]() . So we
may estimate the values of the coefficients
. So we
may estimate the values of the coefficients ![]() and
and ![]() by solving
the system
by solving
the system
![]() for
for ![]() , by
the mean squares method. We can estimate
, by
the mean squares method. We can estimate ![]() and its derivatives in
the same way, using functions
and its derivatives in
the same way, using functions ![]()
![]() such that
such that
![]() for
for ![]() and
and
![]() for
for
![]() , with
, with
![]() .
.
In practice we have used
![]() , the integration being done
between
, the integration being done
between ![]() and the current time. A good approximation of the
integrals is obtained by integrating the system
and the current time. A good approximation of the
integrals is obtained by integrating the system
![]()
![]() if
if ![]() , with
initial conditions
, with
initial conditions ![]() :
: ![]() tends quickly to
tends quickly to
![]() for
for ![]() great enough. Numerical simulations
are given at example 1.
great enough. Numerical simulations
are given at example 1.
In section 3, we consider a delay system
![]() , with
, with ![]() . We use the notation
. We use the notation
![]() , where
, where ![]() is such that
is such that
![]() , for
, for
![]() with
with ![]() . Let
. Let
![]() denote the equation
denote the equation
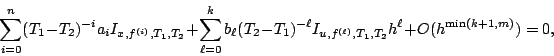
In example 2, we used ![]() and investigate the precision of
the evaluation depending on the size of the noise. See Tableau 1.
and investigate the precision of
the evaluation depending on the size of the noise. See Tableau 1.
In section 4, we adapt the method of section 1 to the delay situation,
solving the system
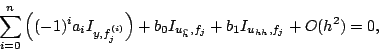
Example 3 shows a simulation with ![]() . Greater delays could be
considered by changing the time scale. Example 4 considers the case of
a slowly varying delay. Scilab simulation files are available at url
[11].
. Greater delays could be
considered by changing the time scale. Example 4 considers the case of
a slowly varying delay. Scilab simulation files are available at url
[11].