- ... diff\'erentielles1
- Un autre article posthume
de l'Ill. Jacobi portant sur le même sujet et contenant les
démonstrations de propositions énoncées ici se trouve dans
les Diarii mathematicii vol. LXIV p. 297. (cf. ce vol. p. 191
[«De investigando ordine systematis aequationum
differentialum», C.G.J. Jacobi's gesammelte Werke,
fünfter Band, herausgegeben von K. Weierstrass, Berlin, Bruck
und Verlag von Georg Reimer, 1890, p. 191-216])
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Jacobi.2
-
Traduit du latin par F. Ollivier (CNRS), FRE CNRS 2341, École
polytechnique, 91128 Palaiseau CEDEX,
mél. francois.ollivier@stix.polytechnique.fr avec l'aide
d'Alexandre Sedoglavic, LIFL, UMR CNRS 8022, Université des Sciences
et Technologies de Lille, 59655 Villeneuve d'Ascq CEDEX,
mél. sedoglav@lifl.fr. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...»3
- §§. 30-33 de l'article cité, Jour. Crelle,
vol. XXIX, ou cette éd. vol. IV p. 495 et suiv. [«Theoria
novi multiplicatoris systemati aequationum differentialum
vulgarium applicandi», C.G.J. Jacobi's gesammelte Werke, vierter Band, herausgegeben von
K. Weierstrass, Berlin, Bruck und Verlag von Georg Reimer, 1890,
p. 495-509].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
deux4
- S'il y a au moins deux variables et si chacune d'elle
n'intervient pas dans une unique équation, les ordres sur les
dérivées
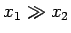 et
et
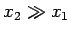 fournissent deux
formes normales différentes, la première contenant une équation ne
dépendant que de
fournissent deux
formes normales différentes, la première contenant une équation ne
dépendant que de 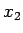 , la seconde une équation ne dépendant que
de
, la seconde une équation ne dépendant que
de 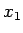 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...\space 5
- La préparation
appliquée, par laquelle le tableau carré
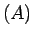 a été
changé en tableau
a été
changé en tableau 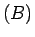 , fait que
, fait que 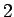 soit la valeur minimale de ce
nombre, cette valeur apparaissant si tous les maxima se trouvent dans
la même série horizontale et si en outre, dans une verticale tous
les termes sont égaux entre eux. Voir Diarium math. vol. LXIV
p.
soit la valeur minimale de ce
nombre, cette valeur apparaissant si tous les maxima se trouvent dans
la même série horizontale et si en outre, dans une verticale tous
les termes sont égaux entre eux. Voir Diarium math. vol. LXIV
p. 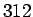 ou ce vol. p.
ou ce vol. p. 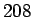 . [Notre traduction p. ???]
. [Notre traduction p. ???]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... s\'eries6
- À ceci près que toutes
les séries depuis lesquelles on passe à celle-ci passent dans
la troisième classe. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
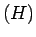 7
7
- l'explication
des signes
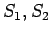 etc. employés dans la table du
carré
etc. employés dans la table du
carré 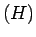 sera fournie dans le paragraphe suivant.
sera fournie dans le paragraphe suivant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complets8
- c'est-à-dire composés de
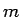 termes.
termes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... auxiliaires9
- À chaque système de maxima
transversaux, on associe un ordre sur les dérivées tels que les
dérivées considérées soient maximales et il lui correspond une forme
normale. E.g., pour le syst`me
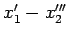 ,
,
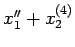 , on a pour
, on a pour
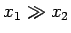 la forme normale
la forme normale
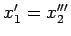 ,
, 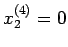 et pour
et pour
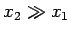 la forme normale
la forme normale
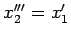 ,
,
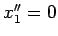 . N.d.T.
. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
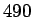 10
10
- Il
s'agit du système page
![[*]](/usr/share/latex2html/icons/crossref.png) . N.d.T.
. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hautes11
- Des formes normales. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... diff\'erentes12
- Il faut
entendre que l'on peut en choisir de la sorte. Toute cette construction
suppose que le déterminant Jacobien par rapport aux dérivées de
têtes est non nul. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... carré
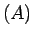 13
13
- L'ordre de l'équation
doit être l'ordre du système. Ceci suppose que
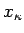 est un
élément primitif. Une condition nécessaire est que toutes les séries
soient attachées à la
est un
élément primitif. Une condition nécessaire est que toutes les séries
soient attachées à la 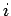
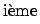 Mais on ne peut
fournir une condition aussi simple que la non nullité d'un déterminant
jacobien..N.d.T.
Mais on ne peut
fournir une condition aussi simple que la non nullité d'un déterminant
jacobien..N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... supprimons14
- Dans
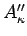 . N.d.T.
. N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... constante15
- Ceci n'est bien sûr vrai que «
génériquement».
N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tronqu\'e16
- Determinans mutilatum. On trouve dans l'article «De investigando...»,
la même notion exprimée par un autre mot :
determinans mancum (p. 197). N.d.T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
petit.17
- Jacobi exclut donc clairement le cas des composantes
singulières «isolées», pour ne prendre en compte que ce que les
algébristes appelleraient la «composante
principale». E.g. l'équation
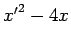 possède une solution
particulière
possède une solution
particulière 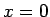 , d'ordre inférieur, qui n'est pas un cas limite de
la solution générale
, d'ordre inférieur, qui n'est pas un cas limite de
la solution générale
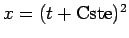 et qui annule le
déterminant tronqué, qui n'est autre ici que lle séparant.
et qui annule le
déterminant tronqué, qui n'est autre ici que lle séparant.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.