Computing derivatives of functions defined with "piecewise" in Maple 

Clara Masse, John Masse and François Ollivier 

Using a naive procedure 

>

 

(1)

 

Operators "diff" and "D" do not act exactly in the same way. 

>

 

(2)

 

>

 

(3)

 

A less naive procedure 

>

 

(4)

 

>

 

(5)

 

Translation in Fortran 

>

 

>

 

doubleprecision function F (x)

 

integer x        if (x .ne. 0) then          F = (0.1D1 - cos(dble(x))) / dble(x)          return        else          F = dble(x * (x ** 8 - 90 * x ** 6 + 5040 * x ** 4 - 151200 *     #x ** 2 + 1814400)) / 0.3628800D7          return        end if      end

 

Using "piecewise" 

>

 

(6)

 

>

 

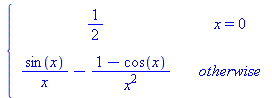(7)

 

>

 

(8)

 

>

 

(9)

 

>

 

 

Warning, procedure/module options ignored
doubleprecision function G (x)        integer x        if (x .ne. 0) then          G = (0.1D1 - cos(dble(x))) / dble(x)          return        else          G = 0.0D0          return        end if      end

 

>

 

(10)

 

>

 

doubleprecision function H (x)        integer x

 

if (0.1D0 .lt. dble(abs(x))) then          H = (0.1D1 - cos(dble(x))) / dble(x)          return        else          H = dble(x * (x ** 8 - 90 * x ** 6 + 5040 * x ** 4 - 151200 *     #x ** 2 + 1814400)) / 0.3628800D7          return        end if      end

 

>