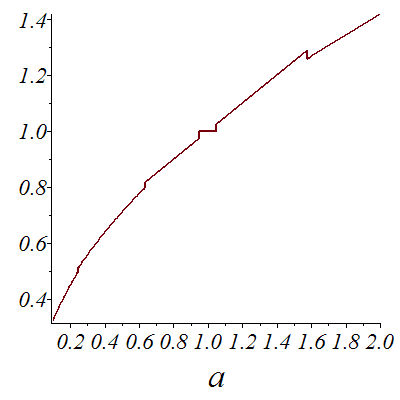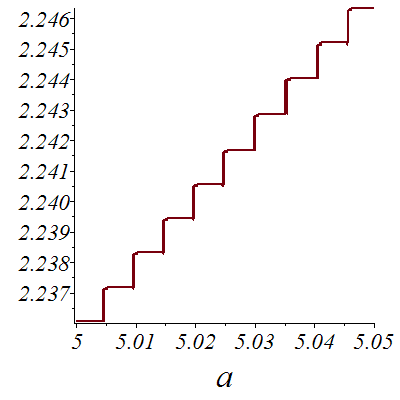Newton2.mw
Illustration of Newton's method
Clara Masse, John Masse and François Ollivier
The classical use of Newton's method for computing square roots. For non numeric arguments g(a,epsilon,c) just returns g(a,epsilon,c) : 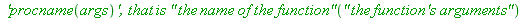
The derivative is defined.
| > |
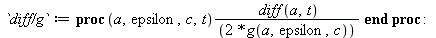 |
We check that the result is correct.
| > |
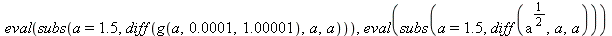 |
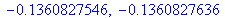 |
(1) |
Discontinuities are related to different numbers of iterations of the Newton operator.
| > |
![plot(g(a, 0.5e-1, 1.), a = .1 .. 2.000, font = [TIMES, ITALIC, 18], labelfont = [TIMES, ITALIC, 26])](images/Newton2_10.gif) |
A "memory" version that start from the last computed value to save time.
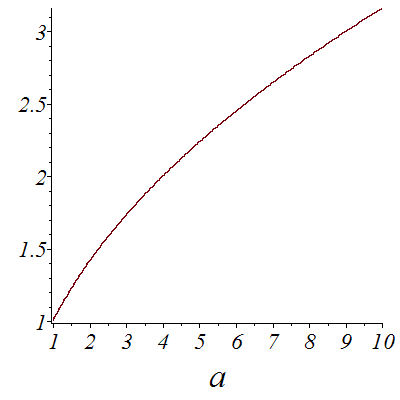
The curve looks smooth.
| > |
![plot(g2(a, 0.1e-2), a = 1 .. 10, font = [TIMES, ITALIC, 18], labelfont = [TIMES, ITALIC, 26])](images/Newton2_17.gif) |
But is has many discontinuities and a derivative that is 0 where it is defined!
| > |
![plot(g2(a, 0.1e-2), a = 5.0 .. 5.05, font = [TIMES, ITALIC, 18], labelfont = [TIMES, ITALIC, 26])](images/Newton2_19.gif) |
Computing derivations with the "RootOf" Maple function, which is used when no closed form solution is found by "solve".
| > |
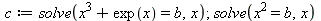 |
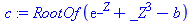 |
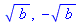 |
(2) |
The results are correct!
| > |
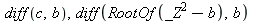 |
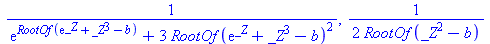 |
(3) |
Trying to look at Maple's internal definitions.
| > |
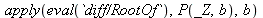 |
)(RootOf(P(_Z, b)), b)), `*`((D[1](P))(RootOf(P(_Z, b)), b)))))](images/Newton2_27.gif) |
(4) |
A "power series" version of our Newton operator, used to compute higher order derivatives. The global variable "nIter" keeps the number of iterations.
Computing the derivative of order 20.
| > |
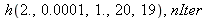 |
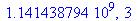 |
(5) |
| > |
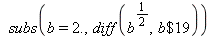 |
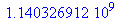 |
(6) |
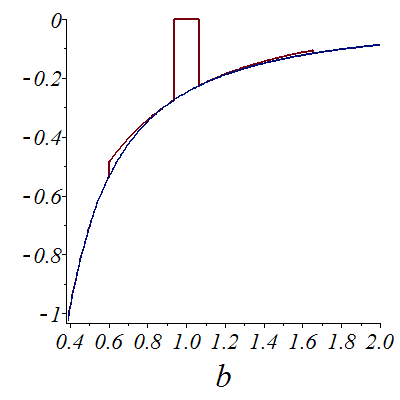
The derivative of the square root function computed with Newton compared with the actual values. The result is false near initial value 1. where no ieration is computed.
| > |
![plot([h(b, 0.1e-2, 1., 10, 2), diff(`*`(`^`(b, `/`(1, 2))), `$`(b, 2))], b = .39 .. 2.00, axes = framed, font = [TIMES, ITALIC, 18], labelfont = [TIMES, ITALIC, 26])](images/Newton2_38.gif)
![plot([h(b, 0.1e-2, 1., 10, 2), diff(`*`(`^`(b, `/`(1, 2))), `$`(b, 2))], b = .39 .. 2.00, axes = framed, font = [TIMES, ITALIC, 18], labelfont = [TIMES, ITALIC, 26])](images/Newton2_39.gif) |
![]()