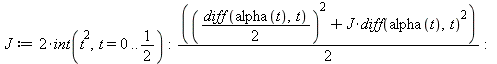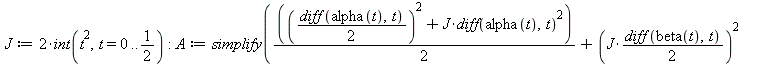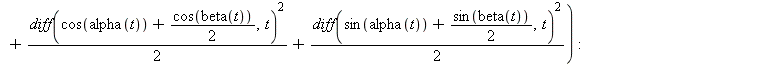Lagrangian.mw

Exemples d'utilisation du package D_ODE_Tools. 

 

Clara MASSE, John MASSE, François OLLIVIER 

 

> read
 

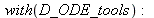> with(D_ODE_tools); -1
 

The "discontinuous" function from Package D_ODE_tools will be used to model Heaviside function. It uses global variables in order to provide information to function "LagrangeDisc" in order to produce "events" in Maple format describing changes of speed when the potential energy function is discontinuous. The next function is an approximation of the Heaviside function using "arctan". 

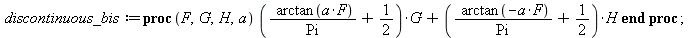> discontinuous_bis := proc (F, G, H, a) `+`(`*`(`+`(`/`(`*`(arctan(`*`(a, `*`(F)))), `*`(Pi)), `/`(1, 2)), `*`(G)), `*`(`+`(`/`(`*`(arctan(`+`(`-`(`*`(a, `*`(F)))))), `*`(Pi)), `/`(1, 2)), `*`(H))) end...
 

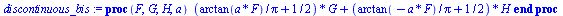proc (F, G, H, a) `+`(`*`(`+`(`/`(`*`(arctan(`*`(a, `*`(F)))), `*`(Pi)), `/`(1, 2)), `*`(G)), `*`(`+`(`/`(`*`(arctan(`+`(`-`(`*`(a, `*`(F)))))), `*`(Pi)), `/`(1, 2)), `*`(H))) end proc (1)
 

We model here a double pendulum using the Lagrangian formalism. 

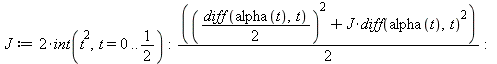> J := `+`(`*`(2, `*`(int(`*`(`^`(t, 2)), t = 0 .. `/`(1, 2))))); -1; `*`(`+`(`^`(`+`(`*`(`/`(1, 2), `*`(diff(alpha(t), t)))), 2), `*`(J, `*`(`^`(diff(alpha(t), t), 2)))), `/`(1, 2)); -1
 

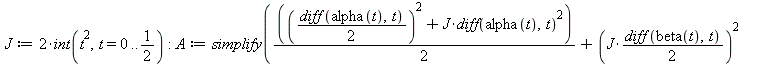
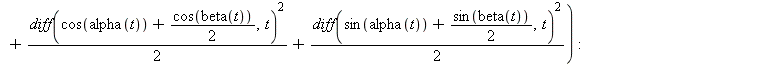> J := `+`(`*`(2, `*`(int(`*`(`^`(t, 2)), t = 0 .. `/`(1, 2))))); -1; A := simplify(`+`(`*`(`+`(`^`(`+`(`*`(`/`(1, 2), `*`(diff(alpha(t), t)))), 2), `*`(J, `*`(`^`(diff(alpha(t), t), 2)))), `/`(1, 2)), ...
J := `+`(`*`(2, `*`(int(`*`(`^`(t, 2)), t = 0 .. `/`(1, 2))))); -1; A := simplify(`+`(`*`(`+`(`^`(`+`(`*`(`/`(1, 2), `*`(diff(alpha(t), t)))), 2), `*`(J, `*`(`^`(diff(alpha(t), t), 2)))), `/`(1, 2)), ...
 

Some discrete variable b(t) is used here to prevent successive unwanted use of different events at the same discontinuity. The parameter "epsilon" of function "LagrangeDisc" imposes an interval between two "events", here set to 0.1. There will be a shock à t=0. as the potential function has a discontinuity. 

> eve := LagrangeDisc(`+`(A, `-`(discontinuous(`+`(sin(alpha(t)), sin(beta(t)), `-`(t)), 0, 10., t, t))), [alpha(t), beta(t)], t, b(t), .1); -1
eve := LagrangeDisc(`+`(A, `-`(discontinuous(`+`(sin(alpha(t)), sin(beta(t)), `-`(t)), 0, 10., t, t))), [alpha(t), beta(t)], t, b(t), .1); -1
 

> syst1 := Lagrange(A, [alpha(t), beta(t)], t); -1
 

Discrete variable b(t) must be declared to dsolve, as well as the "known" function "discontinuous". 

> resu1 := dsolve({op(syst1), alpha(-.1) = 0., b(-.1) = -.2, beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, events = eve, known = discontinuous, discrete_variables = [b(t)]); 1
resu1 := dsolve({op(syst1), alpha(-.1) = 0., b(-.1) = -.2, beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, events = eve, known = discontinuous, discrete_variables = [b(t)]); 1
 

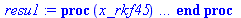proc (x_rkf45) local _res, _dat, _vars, _solnproc, _xout, _ndsol, _pars, _n, _i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; if `<`(1, nargs) then error (2)
 

> resu1(0.); 1; resu1(.1); 1; resu1(.2); 1; resu1(.5); 1; resu1(eventfired = [1, 2, 3, 4]); 1
 

 

 

 

 

[t = 0., alpha(t) = HFloat(0.0), diff(alpha(t), t) = HFloat(-0.8402366863905327), beta(t) = HFloat(0.0), diff(beta(t), t) = HFloat(2.840236686390533), b(t) = HFloat(0.1)]
[t = 0., alpha(t) = HFloat(0.0), diff(alpha(t), t) = HFloat(-0.8402366863905327), beta(t) = HFloat(0.0), diff(beta(t), t) = HFloat(2.840236686390533), b(t) = HFloat(0.1)]
[t = .1, alpha(t) = HFloat(-0.07729738591502781), diff(alpha(t), t) = HFloat(-0.6627710187265853), beta(t) = HFloat(0.27026295691730523), diff(beta(t), t) = HFloat(2.480558179427595), b(t) = HFloat(0....
[t = .1, alpha(t) = HFloat(-0.07729738591502781), diff(alpha(t), t) = HFloat(-0.6627710187265853), beta(t) = HFloat(0.27026295691730523), diff(beta(t), t) = HFloat(2.480558179427595), b(t) = HFloat(0....
[t = .2, alpha(t) = HFloat(-0.13153139343253553), diff(alpha(t), t) = HFloat(-0.4333574558303768), beta(t) = HFloat(0.49548459071708634), diff(beta(t), t) = HFloat(2.054911319233998), b(t) = HFloat(0....
[t = .2, alpha(t) = HFloat(-0.13153139343253553), diff(alpha(t), t) = HFloat(-0.4333574558303768), beta(t) = HFloat(0.49548459071708634), diff(beta(t), t) = HFloat(2.054911319233998), b(t) = HFloat(0....
[t = .5, alpha(t) = HFloat(-0.19643657258363303), diff(alpha(t), t) = HFloat(-0.04599108710477836), beta(t) = HFloat(1.0197585865274654), diff(beta(t), t) = HFloat(1.5662422247926704), b(t) = HFloat(0...
[t = .5, alpha(t) = HFloat(-0.19643657258363303), diff(alpha(t), t) = HFloat(-0.04599108710477836), beta(t) = HFloat(1.0197585865274654), diff(beta(t), t) = HFloat(1.5662422247926704), b(t) = HFloat(0...
[HFloat(-0.1), HFloat(-0.1), HFloat(-0.1), HFloat(0.0)] (3)
 

We compare with the results obtained using the "arctan" approximation of Heaviside function. This is a simple way to test our implementation and also the validity of using "arctan". Results are correct with a relative error of 10^-3 for 0.1, 0.2 and 0.5. 

> syst2 := Lagrange(`+`(A, `-`(discontinuous_bis(`+`(alpha(t), beta(t), `-`(t)), 0, 10., 100000))), [alpha(t), beta(t)], t); -1
 

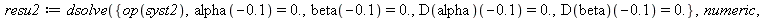
> resu2 := dsolve({op(syst2), alpha(-.1) = 0., beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, known = discontinuous_bis); 1
resu2 := dsolve({op(syst2), alpha(-.1) = 0., beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, known = discontinuous_bis); 1
 

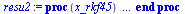proc (x_rkf45) local _res, _dat, _vars, _solnproc, _xout, _ndsol, _pars, _n, _i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; if `<`(1, nargs) then error (4)
 

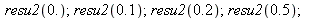> resu2(0.); 1; resu2(.1); 1; resu2(.2); 1; resu2(.5); 1
 

 

 

 

[t = 0., alpha(t) = HFloat(-3.714939674095793e-4), diff(alpha(t), t) = HFloat(-0.11600605601764907), beta(t) = HFloat(0.0012557554799972513), diff(beta(t), t) = HFloat(0.3921343169949242)]
[t = 0., alpha(t) = HFloat(-3.714939674095793e-4), diff(alpha(t), t) = HFloat(-0.11600605601764907), beta(t) = HFloat(0.0012557554799972513), diff(beta(t), t) = HFloat(0.3921343169949242)]
[t = .1, alpha(t) = HFloat(-0.0766166333402536), diff(alpha(t), t) = HFloat(-0.6653506501070379), beta(t) = HFloat(0.2677293805979707), diff(beta(t), t) = HFloat(2.485775938847936)]
[t = .1, alpha(t) = HFloat(-0.0766166333402536), diff(alpha(t), t) = HFloat(-0.6653506501070379), beta(t) = HFloat(0.2677293805979707), diff(beta(t), t) = HFloat(2.485775938847936)]
[t = .2, alpha(t) = HFloat(-0.13109396965726605), diff(alpha(t), t) = HFloat(-0.43543460138432694), beta(t) = HFloat(0.49346432380943966), diff(beta(t), t) = HFloat(2.0594316355741085)]
[t = .2, alpha(t) = HFloat(-0.13109396965726605), diff(alpha(t), t) = HFloat(-0.43543460138432694), beta(t) = HFloat(0.49346432380943966), diff(beta(t), t) = HFloat(2.0594316355741085)]
[t = .5, alpha(t) = HFloat(-0.19635554824400617), diff(alpha(t), t) = HFloat(-0.046571225776342824), beta(t) = HFloat(1.0186388982885444), diff(beta(t), t) = HFloat(1.5683705269616137)]
[t = .5, alpha(t) = HFloat(-0.19635554824400617), diff(alpha(t), t) = HFloat(-0.046571225776342824), beta(t) = HFloat(1.0186388982885444), diff(beta(t), t) = HFloat(1.5683705269616137)]		 (5)
 

We repeat with coeffiicient a= 10^6 in "discontinuous_bis". 

> syst2 := Lagrange(`+`(A, `-`(discontinuous_bis(`+`(alpha(t), beta(t), `-`(t)), 0, 10., `^`(10, 6)))), [alpha(t), beta(t)], t); -1
 

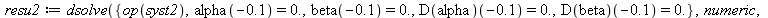
> resu2 := dsolve({op(syst2), alpha(-.1) = 0., beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, known = discontinuous_bis); 1
resu2 := dsolve({op(syst2), alpha(-.1) = 0., beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, known = discontinuous_bis); 1
 

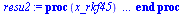proc (x_rkf45) local _res, _dat, _vars, _solnproc, _xout, _ndsol, _pars, _n, _i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; if `<`(1, nargs) then error (6)
 

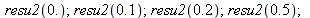> resu2(0.); 1; resu2(.1); 1; resu2(.2); 1; resu2(.5); 1
 

 

 

 

[t = 0., alpha(t) = HFloat(-5.320373706085857e-5), diff(alpha(t), t) = HFloat(-0.07750225309351719), beta(t) = HFloat(1.7984362198564553e-4), diff(beta(t), t) = HFloat(0.2619794638065434)]
[t = 0., alpha(t) = HFloat(-5.320373706085857e-5), diff(alpha(t), t) = HFloat(-0.07750225309351719), beta(t) = HFloat(1.7984362198564553e-4), diff(beta(t), t) = HFloat(0.2619794638065434)]
[t = .1, alpha(t) = HFloat(-0.07719660827621888), diff(alpha(t), t) = HFloat(-0.6631574643695163), beta(t) = HFloat(0.26988687523332355), diff(beta(t), t) = HFloat(2.481333004240383)]
[t = .1, alpha(t) = HFloat(-0.07719660827621888), diff(alpha(t), t) = HFloat(-0.6631574643695163), beta(t) = HFloat(0.26988687523332355), diff(beta(t), t) = HFloat(2.481333004240383)]
[t = .2, alpha(t) = HFloat(-0.13146634724654552), diff(alpha(t), t) = HFloat(-0.4336608898928197), beta(t) = HFloat(0.4951808749059904), diff(beta(t), t) = HFloat(2.0555251903692735)]
[t = .2, alpha(t) = HFloat(-0.13146634724654552), diff(alpha(t), t) = HFloat(-0.4336608898928197), beta(t) = HFloat(0.4951808749059904), diff(beta(t), t) = HFloat(2.0555251903692735)]
[t = .5, alpha(t) = HFloat(-0.19642646055685933), diff(alpha(t), t) = HFloat(-0.04609677448460031), beta(t) = HFloat(1.019568612605924), diff(beta(t), t) = HFloat(1.5664859368309014)]
[t = .5, alpha(t) = HFloat(-0.19642646055685933), diff(alpha(t), t) = HFloat(-0.04609677448460031), beta(t) = HFloat(1.019568612605924), diff(beta(t), t) = HFloat(1.5664859368309014)]		 (7)
 

Now with a=10^9. The value obtained for 0.001 is very closed to the the real value at 0. 

> syst2 := Lagrange(`+`(A, `-`(discontinuous_bis(`+`(alpha(t), beta(t), `-`(t)), 0, 10., `^`(10, 9)))), [alpha(t), beta(t)], t); -1
 

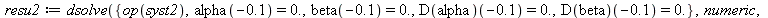
> resu2 := dsolve({op(syst2), alpha(-.1) = 0., beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, known = discontinuous_bis); 1
resu2 := dsolve({op(syst2), alpha(-.1) = 0., beta(-.1) = 0., (D(alpha))(-.1) = 0., (D(beta))(-.1) = 0.}, numeric, known = discontinuous_bis); 1
 

proc (x_rkf45) local _res, _dat, _vars, _solnproc, _xout, _ndsol, _pars, _n, _i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; if `<`(1, nargs) then error (8)
 

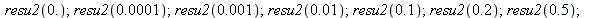> resu2(0.); 1; resu2(0.1e-3); 1; resu2(0.1e-2); 1; resu2(0.1e-1); 1; resu2(.1); 1; resu2(.2); 1; resu2(.5); 1
 

 

 

 

 

 

 

[t = 0., alpha(t) = HFloat(-1.0714166312483449e-7), diff(alpha(t), t) = HFloat(-0.036572261486332344), beta(t) = HFloat(3.6216900215007507e-7), diff(beta(t), t) = HFloat(0.12362454588227215)]
[t = 0., alpha(t) = HFloat(-1.0714166312483449e-7), diff(alpha(t), t) = HFloat(-0.036572261486332344), beta(t) = HFloat(3.6216900215007507e-7), diff(beta(t), t) = HFloat(0.12362454588227215)]
[t = 0.1e-3, alpha(t) = HFloat(-8.382563371655524e-5), diff(alpha(t), t) = HFloat(-0.8401471331567437), beta(t) = HFloat(2.8335426568469114e-4), diff(beta(t), t) = HFloat(2.8399342974085036)]
[t = 0.1e-3, alpha(t) = HFloat(-8.382563371655524e-5), diff(alpha(t), t) = HFloat(-0.8401471331567437), beta(t) = HFloat(2.8335426568469114e-4), diff(beta(t), t) = HFloat(2.8399342974085036)]
[t = 0.1e-2, alpha(t) = HFloat(-8.400100333244134e-4), diff(alpha(t), t) = HFloat(-0.840203042561481), beta(t) = HFloat(0.002839481441257134), diff(beta(t), t) = HFloat(2.8401556859520496)]
[t = 0.1e-2, alpha(t) = HFloat(-8.400100333244134e-4), diff(alpha(t), t) = HFloat(-0.840203042561481), beta(t) = HFloat(0.002839481441257134), diff(beta(t), t) = HFloat(2.8401556859520496)]
[t = 0.1e-1, alpha(t) = HFloat(-0.00839379367003894), diff(alpha(t), t) = HFloat(-0.8377392528997166), beta(t) = HFloat(0.02838427454473319), diff(beta(t), t) = HFloat(2.835055765857525)]
[t = 0.1e-1, alpha(t) = HFloat(-0.00839379367003894), diff(alpha(t), t) = HFloat(-0.8377392528997166), beta(t) = HFloat(0.02838427454473319), diff(beta(t), t) = HFloat(2.835055765857525)]
[t = .1, alpha(t) = HFloat(-0.07729720365675165), diff(alpha(t), t) = HFloat(-0.6627717765435983), beta(t) = HFloat(0.27026228383826434), diff(beta(t), t) = HFloat(2.4805599912864613)]
[t = .1, alpha(t) = HFloat(-0.07729720365675165), diff(alpha(t), t) = HFloat(-0.6627717765435983), beta(t) = HFloat(0.27026228383826434), diff(beta(t), t) = HFloat(2.4805599912864613)]
[t = .2, alpha(t) = HFloat(-0.13153129399502025), diff(alpha(t), t) = HFloat(-0.4333580722500373), beta(t) = HFloat(0.49548411851254504), diff(beta(t), t) = HFloat(2.054912887174654)]
[t = .2, alpha(t) = HFloat(-0.13153129399502025), diff(alpha(t), t) = HFloat(-0.4333580722500373), beta(t) = HFloat(0.49548411851254504), diff(beta(t), t) = HFloat(2.054912887174654)]
[t = .5, alpha(t) = HFloat(-0.19643656285648153), diff(alpha(t), t) = HFloat(-0.04599121029523719), beta(t) = HFloat(1.0197584137361428), diff(beta(t), t) = HFloat(1.5662430154469584)]
[t = .5, alpha(t) = HFloat(-0.19643656285648153), diff(alpha(t), t) = HFloat(-0.04599121029523719), beta(t) = HFloat(1.0197584137361428), diff(beta(t), t) = HFloat(1.5662430154469584)]		 (9)
 

A general study of the advantages and drawbacks of these two approaches remains to be done, both from the standpoint of computation time and precision.