Perelson_3_numeric.mw
Work in progress with Hervé Le Meur (Orsay)
Identifiability criteria for models of HIV virus, after Perelson et al.
One of Perelson's model. We assume here that all variables T, Ta and V are observed. We don't claim that the hypotheses are meaningfull in biology. We just try to illustrate a computational method.
| > |
![Cond_init := [T(0) = T0, Ta(0) = Ta0, V(0) = V0]; -1](images/Perelson_3_numeric_4.gif) |
| > |
![L_params := [T0, Ta0, V0, beta, rho, delta, c, N, lambda]; -1](images/Perelson_3_numeric_5.gif) |
| > |
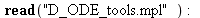 |
| > |
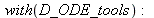 |
| > |
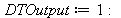 |
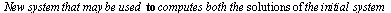 and the values of derivatives of these solutions with respect to parameters.
and the values of derivatives of these solutions with respect to parameters.
| > |
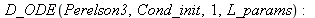 |
| > |
 |
| > |
![resu2(parameters = [180, 20, 50000, 0.2e-4, .15, .55, 5.5, 900, 80]); -1](images/Perelson_3_numeric_12.gif) |
Manipulating the result, something is wrong.
| > |
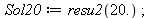 |
We want to compute a 9*9 determinant, so we will use substitution to extract derivatives values from the result.
| > |
); 1](images/Perelson_3_numeric_21.gif) |
](images/Perelson_3_numeric_22.gif) |
(2) |
The substitution was not done. Why?
| > |
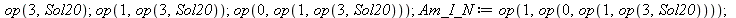 |
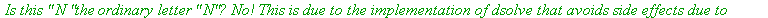

| > |
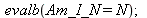 |
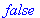 |
(4) |
We need to use a trick: with global variable DTOutput set to 0, the parameter N is replaced by _N.
| > |
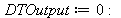 |
| > |
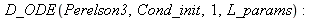 |
| > |
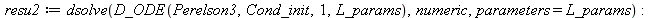 |
| > |
![resu2(parameters = [180, 20, 50000, 0.2e-4, .15, .55, 5.5, 900, 80]); -1](images/Perelson_3_numeric_35.gif) |
| > |
![L_Sol := [resu2(0.), resu2(10.), resu2(20.)]; -1](images/Perelson_3_numeric_36.gif) |
| > |
![L_var := [T, Ta, V]; -1](images/Perelson_3_numeric_37.gif) |
| > |
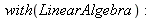 |
This time, we can make substitutions with our result safely.
| > |
), `in`(var, L_var)), `in`(sol, L_Sol))], `in`(par, L_params))])); 1](images/Perelson_3_numeric_39.gif) |
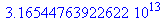 |
(5) |
The determinant is non 0, which shows that the model is both identifiable and observable.
![]() and the values of derivatives of these solutions with respect to parameters.
and the values of derivatives of these solutions with respect to parameters. ![]()
![]()