This column is also available in pdf: filename MahalanobisThalesTheorem.pdf
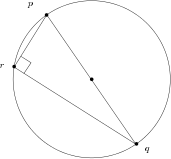
In planar Euclidean geometry, Thales’ theorem states that any triangle pqr circumscribing a circle with one pair (p,q) of antipodal points is necessarily a right triangle. A pair (p,q) of antipodal points of a smooth convex object is such that the tangent lines at p and q are parallel to each other. See Figure 1 for an illustration, and [3] for a historical account (Thales of Miletus, 624–546 BC).
Theorem 1 (Thales’ circle theorem) Any triangle circumscribed by a circle with one side being a diameter is right-angle.

Let DA(p,q) denote the Mahalanobis distance between two points p and q, for a positive definite matrix A ≻ 0:
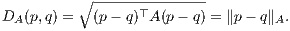
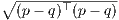 .
.
A Mahalanobis circle [2] CA(c,r) of center c and radius r is defined as follows:
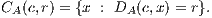
Let us generalize Thales’ theorem as follows:
Theorem 2 (Thales’ Mahalanobis circle theorem) Any triangle circumscribed by a Mahalanobis circle with one pair of points being antipodal is right-angle.
Proof: Consider the Cholesky decomposition of A: A = LL⊤ = U⊤U with L (U = L⊤) a lower triangular matrix (an upper triangular matrix, respectively) with positive diagonal elements. The Mahalanobis distance amounts to calculate an ordinary Euclidean distance on affinely transformed points x′ = L⊤x = Ux:
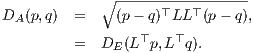
Thus a Mahalanobis circles CA transforms affinely to a Euclidean circle CE = CI, and antipodal pairs of points on CA remain antipodal in CE.
Two vectors u and v are perpendicular in the Mahalanobis geometry if and only if u⊤Av = 0. That is, if u⊤Av = u⊤LL⊤v = (L⊤u)⊤L⊤v = u′⊤v′ = 0.
A triangle pqr circumscribing the Mahalanobis circle CA with (p,q) an antipodal pair in Mahalanobis geometry transforms into a triangle p′q′r′ circumscribing the Euclidean circle C′ = {L⊤x : x ∈ CA(c,r)} with (p′,q′) an antipodal pair. Therefore p′q′r′ is a right-angle triangle in Euclidean geometry, and:
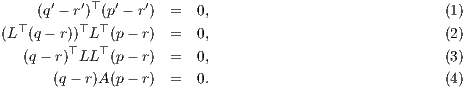
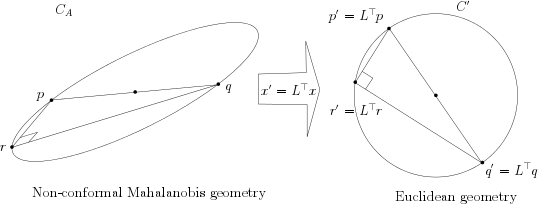
Note that Mahalanobis geometry is not conformal when A ⁄= λI (for λ > 0), the scaled identity matrix. Therefore angles are not preserved in Mahalanobis geometry: That is, a Mahalanobis right-angle cannot be visualized as a Euclidean right-angle in general.
Squared Mahalanobis distances are the only symmetric Bregman divergences [1]. But Thales’ theorem do not extend to other (asymmetric) Bregman divergences.
[1] Jean-Daniel Boissonnat, Frank Nielsen, and Richard Nock. Bregman Voronoi diagrams. Discrete & Computational Geometry, 44(2):281–307, 2010.
[2] Frank Nielsen and Richard Nock. On the smallest enclosing information disk. Information Processing Letters, 105(3):93–97, 2008.
[3] Christoph J Scriba and Peter Schreiber. Geometry in the Greek-Hellenistic era and late antiquity. In 5000 Years of Geometry, pages 27–116. Springer, 2015.