Clustering in Hilbert simplex geometry

pdf
by Frank Nielsen and Ke Sun

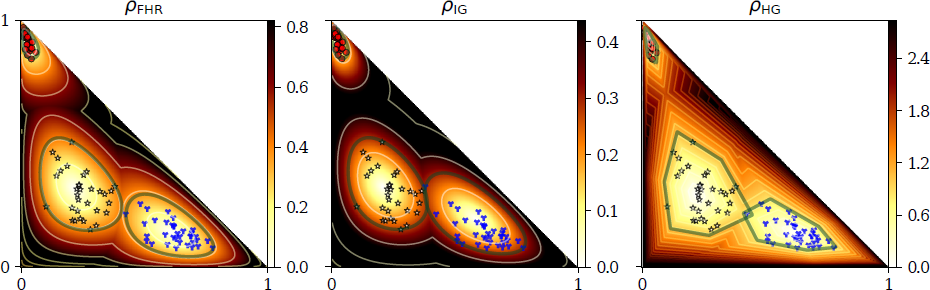
Clustering categorical distributions in the probability simplex is a fundamental primitive often met in applications dealing with histograms or mixtures of multinomials. Traditionally, the differentialgeometric structure of the probability simplex has been used either by (i) setting the Riemannian metric tensor to the Fisher information matrix of the categorical distributions, or (ii) defining the informationgeometric structure induced by a smooth dissimilarity measure, called a divergence. In this paper, we introduce a novel computationally-friendly non-Riemannian framework for modeling the probability simplex: Hilbert simplex geometry. We discuss the pros and cons of those three statistical modelings, and compare them experimentally for clustering tasks.

Keywords: Fisher-Rao geometry, information geometry, Hilbert simplex geometry, center-based clustering.

Python source code

Download the Python code for reproducible research: HilbertSimplexClusteringCode.zip

Last updated, April 2017.