

Le rendez-vous était fixé le mercredi 5 septembre à 11 heures au lycée SLouis, 44. b. SMichel, Paris, métro Luxembourg. Étaient présents :
Ce 5 septembre correspondait à la rentrée des classes au lycée Saint-Louis. Il n'était donc pas question au sein de cette cohue de pouvoir s'installer longuement dans une des salles de l'établissement. Le bar Saint-Louis étant fermé ce jour-là, nous, i.e. Pierre Demers, Paul Depovere, Julien Lalande et moi, nous sommes installés pour déjeuner ensemble à la brasserie L'Écritoire, 3 place de la Sorbonne. Patrick Callet est venu après nous rejoindre pour le café.
J'ai pu rencontrer Pierre Demers pour la première fois ce jour-là, car je ne le connaissais que par email. J'ai profité de l'occasion pour lui donner le fac-similé d'un livre qui se trouve à la bibliothèque centrale de l'X, "Le mystère des nombres élucidés", par Pierre Barthélémy (1983). Ce document, fantaisiste s'il en est, traite entre autres de la classification périodique des éléments en relation avec une représentation des nombres entiers en base huit. Après tout, on peut peut-être y trouver de bonnes idées.
Les autres personnes m'étaient inconnues, et avaient toutes une formation solide en chimie. Le fil de certaines conversations m'a donc parfois échappé. Julien Lalande et Paul Depovere ont notamment discuté de nombreuses réactions chimiques passionnantes, dont certaines que j'avais réalisées en prépa, notamment une réaction avec une solution qui passait par toutes les couleurs à quelques secondes d'intervalle. Je me suis rendu compte de l'aspect ludique que pouvait revêtir les réactions chimiques. Malheureusement, comme 90% des taupins, je suis complètement passé à de la chimie, sans jamais vraiment essayer d'en comprendre l'intérêt.
Dans les photos ci-dessous, on trouve respectivement, de gauche à droite, Paul Depovere, moi-même, Julien Lalande (première photo), et Patrick Callet tenant son appareil photo (seconde photo).


Julien Lalande, professeur de prépa à Saint-Louis, a enseigné quelques années à Condorcet, établissement où j'avais fait ma math-sup et ma maths-spé. Paul Depovere est l'auteur d'un livre sur la classification des éléments chimiques dont j'avais apporté un exemplaire, dans lequel on peut trouver des reproductions de timbres-poste montrant les savants qui ont découvert les différents atomes. Ce livre sert surtout de référence pour retrouver les caractéristiques de chaque élément, y compris les plus récents : il a permis de lever un doute sur le numéro atomique du Bohrium, sur lequel Pierre Demers et Paul Depovere se sont à un moment interrogés. Patrick Callet, qui enseigne à l'École Centrale de Paris, gravite dans un univers proche du mien, autour des universités et des grandes écoles ; il avait d'ailleurs déjà entendu parler du laboratoire dans lequel je travaille.
Une petite polémique s'est engagée à propos de la prononciation du mot "Québécium" : doit-on prononcer le "c" comme un "s" ou comme un "k" ? Pierre Demers tendait à préférer la première prononciation, tandis que Julien Lalande et moi options plutôt pour la seconde. Maintenant, les deux prononciations me semblent également défendables.
Les questions à l'ordre du jour, rédigées
par Pierre Demers quelques jours avant la réunion,
se présentaient ainsi :
(Personne n'a pris de notes, et j'ai quelques jours plus tard
été désigné volontaire pour faire
le compte rendu :)
A. En quoi consiste-t-il? En quoi apporte-t-il un progrès sur
le t. de Mendeleïev? Sa contribution à la science, à la francophonie.
B. Quelles objections peut-on y apporter?
Votre question v.g.
Apporte-t-il un progrès sur le tableau de
Mendeleïev? Indifférence et
routine établie.
Pierre Demers propose une nouvelle disposition des
éléments chimiques. Dans la lignée des mathématiques grecques
et des solides de Platon, il pressent une harmonie sous-jacente
à la classification des éléments, et essaie de la retrouver
dans sa disposition.
Ainsi, il dispose les éléments en plusieurs carrés,
respectivement de 2*2=4, 4*4=16, 6*6=36 et 8*8=64 cases, d'où
en tout 4+16+36+64 = 120 cases, dans lesquels sont disposés
118 éléments.
Il remarque que
4+16=20, et il pense reconnaître dans les nombres 20 et
64 respectivement le nombre d'acides aminés et le nombre de
codons. Il postule donc l'existence de 36 autres molécules ayant
un rôle biologique à jouer. En revanche, il ne va pas jusqu'à
dire qu'il existe une correspondance entre les atomes de la
classification et les molécules biologiques. Il dit juste qu'il
y a là une nécessité mathématique.
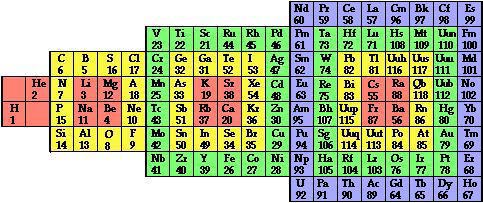
Il est aussi capable de disposer ces 120 éléments en un tétraèdre, décomposé en rhomboèdres. Ces histoires de pavages ne sont pas sans rappeler les quasi-cristaux.


Mes connaissances en chimie ne me permettent pas de comprendre les subtilités de cette nouvelle disposition par rapport à la disposition classique des éléments chimiques. Cependant, il apparaît que, d'un certain point de vue, la disposition de Demers apporte une cohérence que le tableau de Mendeleïev n'a pas, tandis que, d'un autre point de vue, il perd en cohérence par rapport au tableau de Mendeleïev. C'est à Julien Lalande et Paul Depovere de préciser ce point. Je crois seulement me souvenir qu'il y avait une anicroche dans un coin du deuxième carré.
La lecture d'ouvrages de vulgarisation m'avait fait croire que le principe de Pauli associé à l'équation de Schrödinger permettait de rendre compte de la classification périodique des éléments, mais il semblerait que l'on fasse beaucoup d'approximations dans les équations des orbitales, dès que le modèle devient compliqué. Cela n'est pas sans rappeler un problème similaire en théorie quantique des champs où les diagrammes de Feynman abondamment utilisés par les physiciens ne connaissent toujours pas de justification théorique mathématique solide : on soustrait des infinis à des infinis et on dit qu'on obtient des zéros. Autrement dit, le problème de la classification des éléments est loin d'être résolu. L'approche du système du Québécium est donc la bienvenue pour compléter notre connaissance de la classification.
Le système du Québecium semble suffisamment simple pour qu'on se pose la question de l'enseigner dès les petites classes. Cependant cela serait un trop grand risque, car il vaut mieux d'abord enseigner les classiques aux étudiants débutants. Dans le même ordre d'idées, on a pu enseigner de l'analyse non standard à des étudiants de DEUG, ce qui correspond en France aux deux premières années d'études universitaires (undergraduate studies). Ces étudiants ont ensuite connu les pires difficultés en licence, puisqu'il n'étaient pas habitués à manier correctement les epsilons en analyse classique, ne serait-ce que pour démontrer le théorème des valeurs intermédiaires pour les fonctions continues.
Malgré ses vertus pédagogiques, le système du Québecium n'a autant que je sache pas encore permis de conduire à de nouvelles découvertes, en termes de pouvoir de prédiction ou d'expérimentations hors de portée des autres approches. C'est ce type de découverte qui permettrait de lui donner une puissance médiatique.
Un ancien élève de Julien Lalande est passé par hasard pendant notre repas. Un personnage très brillant (major à Ulm), très sympatique, très humble, très ouvert, très cultivé etc., mais Julien Lalande n'a pas jugé bon de lui toucher un mot à propos du système du Québecium. Cette anecdote montre bien que le système du Québecium manque encore de maturité pour connaître un rayonnement trop important.