Logique de Hoare mécanisée
par Jean-Christophe Filliâtre, François Pottier, et Olivier Bouissou
Ce TD met en œuvre la logique de Hoare sur des programmes Java. On commence par annoter le code source Java par des spécifications
formelles ; puis un outil automatique produit un ensemble de formules logiques, appelées obligations de vérification, exprimant la
correction du programme vis-à-vis de cette spécification ; enfin des outils de preuve automatique sont utilisés pour montrer la validité de
ces formules.
Setup
Things that need to be translated into French are written in boxes like these.
Ce TD nécessite des outils qui ont été installés et testés en salles infos. Si vous souhaitez vraiment travailler sur votre portable ou
à distance, le plus simple est certainement de vous connecter sur l'une des machines des salles infos par ssh. L'installation de
certains des logiciels nécessaires est fastidieuse et d'autres ne tournent pas sous Windows.
Nous allons utiliser deux outils :
- le plugin OpenJML pour Eclipse qui permet de construire, à partir d'un programme Java annoté, des
obligations de preuve;
- le solver Z3 qui permet de prouver automatiquement la validité de ces obligations.
ATTENTION : Pour ce TD et seulement
pour ce TD, il est inutile de lancer Eclipse depuis le menu « K ». Utilisez la commande suivante :
/users/profs/info/kaustuv.chaudhuri/bin/td7-eclipse
Pour cela, le plus facile est d'ajouter à votre
PATH le répertoire /users/profs/info/kaustuv.chaudhuri/bin par la ligne:
[loire ~]$ export PATH=/users/profs/info/kaustuv.chaudhuri/bin/:$PATH
(La partie [loire ~]$, c'est l'invite de commande.) Ensuite, vous pourrez lancer Eclipse ainsi:
[loire ~]$ td7-eclipse &
Prérequis : Java 1.7
OpenJML n'est pas encore compatible avec Java 1.8 installé dans les salles infos. Nous avons donc besoin de configurer Eclipse afin
d'utiliser Java 1.7.
- Cliquer sur le menu
Window → Preferences et taper Installed JREs dans le zone de text en haut à
gauche.
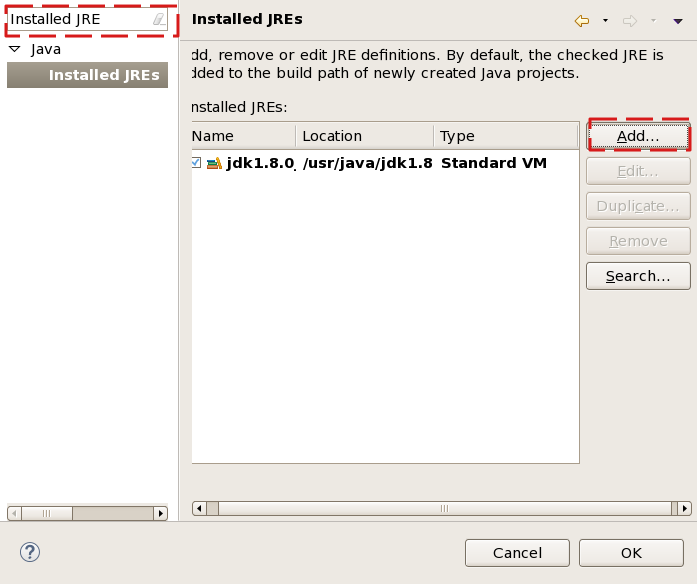
- Cliquer sur
Add puis Standard VM puis Next et mettre deux champs comme ci-dessous:
JRE home: |
/users/profs/info/kaustuv.chaudhuri/jdk1.7.0_79 |
Default VM arguments: |
-ea |
Les champs JRE name et JRE system libraries seront automatiquement remplis.
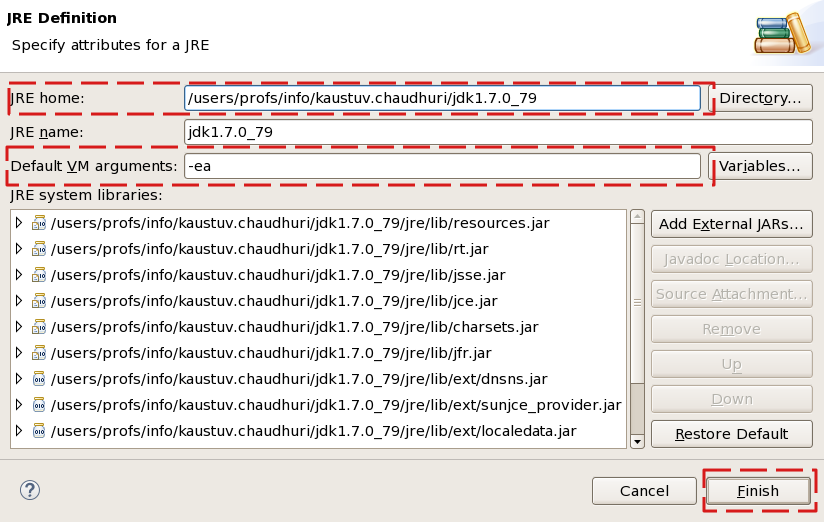
Ignorer les autres champs et boutons et cliquer sur Finish.
- Vous allez voir cela :
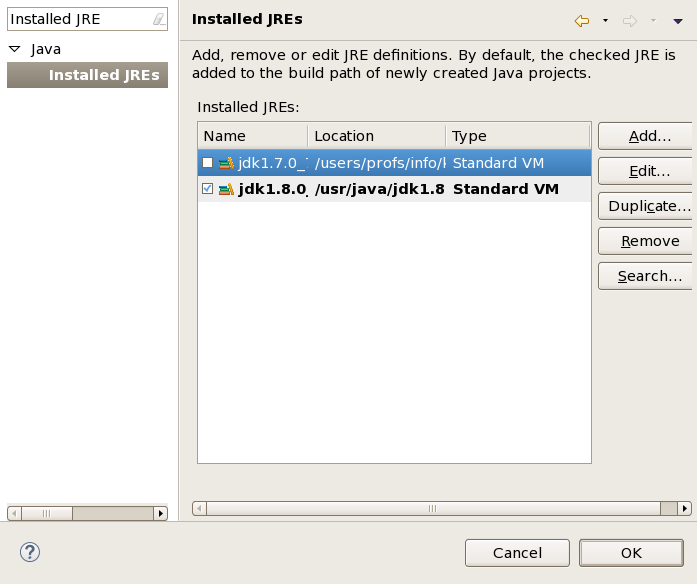
Cliquer sur OK
Installation du plugin OpenJML
Pour commencer, il faut installer le plugin OpenJML pour Eclipse.
- Ouvrir le panneau d'installation des nouveaux plugins en cliquant
Help > Install New Software ; cliquer alors sur le bouton Add.
- Dans la boîte de dialogue, mettre les champs comme çi-dessous:
Name |
OpenJML |
Location |
http://jmlspecs.sourceforge.net/openjml-updatesite |
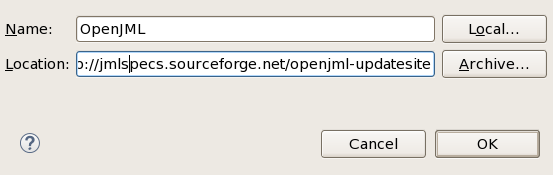
Puis cliquer sur OK.
- Sélectionner
OpenJML et cliquer sur Next (deux fois).
- Accepter la licence "GPL" et cliquer sur
Finish.
- Pendant l'installation, un warning au sujet des programmes non-signées apparaîtra; cliquer sur
OK.
- Redemarrer Eclipse.
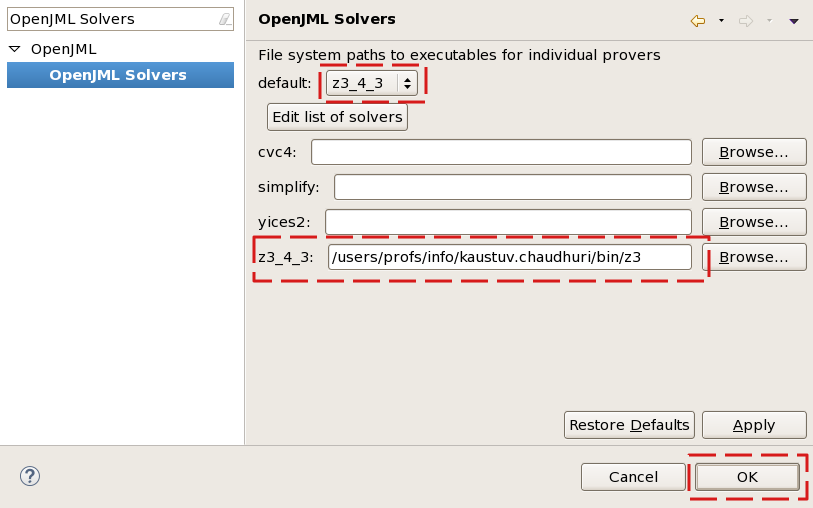
Configuration du plugin OpenJML pour utiliser Z3
Le programme Z3 étant assez compliqué à compiler et installer, nous l'avons fait pour vous. Il n'y a plus qu'à dire à Eclipse et OpenJML
où il se trouve ! Pour cela, ouvrir la fenêtre des préférences d'Eclipse (cliquer sur "Window > Preferences"), et écrire
OpenJML Solvers. Dans le champ z3_4_3, mettre:
/users/profs/info/kaustuv.chaudhuri/bin/z3
puis cliquer sur OK.
Initialisation du Projet TD7 et Utilisation du Plugin
Nous allons maintenant effectuer pas à pas un premier exemple pour montrer comment annoter et vérifier un programme Java.
- Créer un nouveau projet « TD7 » par
File > New > Java Project.
- Sélectionner
Use a project specific JRE et jdk1.7.0_79 dans la liste déroulant.
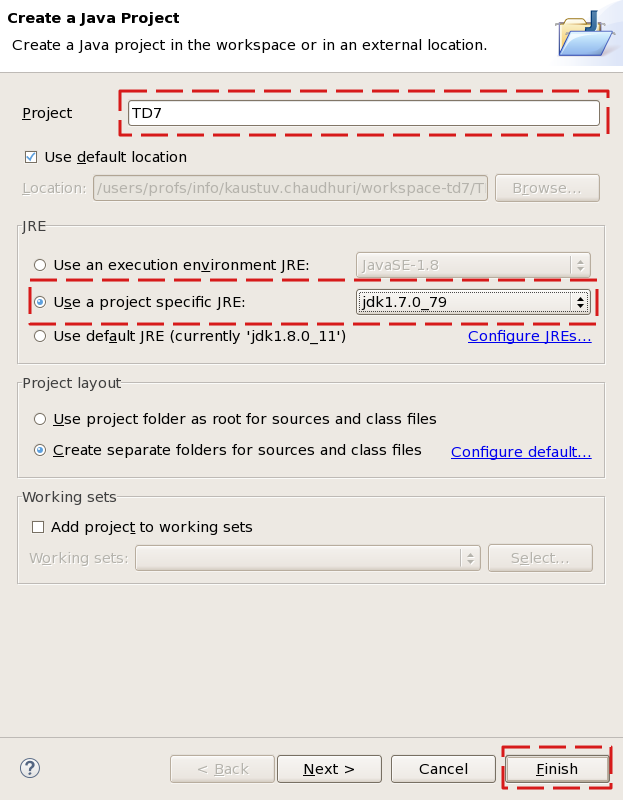
- Ensuite, cliquer sur
Finish.
- Cliquer sur le menu
JML > Enable JML for this Project.
Les annotations sont insérées sous la forme de commentaires particuliers, de la forme /*@ ... */ ou //@. Supposons par
exemple que l'on souhaite vérifier le programme suivant calculant le minimum d'un tableau d'entiers :
class Min {
int getMin(int t[]) {
int res = t[0];
for (int i = 1; i < t.length; i++)
if (t[i] < res) res = t[i];
return res;
}
}
Annotation des méthodes
La première forme d'annotation consiste à associer aux méthodes des pré- et postconditions. Une précondition est une propriété que l'on
suppose vraie au moment où la méthode est appelée. Elle est introduite par le mot clé requires dans une annotation précédant la
méthode. Ainsi
//@ requires t != null && t.length > 0;
int getMin(int t[]) { ... }
indique que la méthode getMin attend un tableau (non null) ayant au moins un élément. Notez la présence du
point-virgule à la fin de l'annotation.
Attention : lors d'un copy-paste depuis ce sujet, Eclipse ajoute parfois un caractère espace avant le caractère @, ce qui
désactive l'annotation correspondante. Pensez à rectifier si besoin.
Une postcondition indique au contraire une propriété garantie par la méthode, une fois son exécution terminée. Elle est introduite par
le mot clé ensures. Ainsi une postcondition (partielle) pour getMin peut être
//@ ensures \forall int i; 0 <= i && i < t.length; \result <= t[i];
int getMin(int t[]) { ... }
Elle exprime que le résultat est plus petit que tout élément de t. Comme on le voit sur cet exemple, la valeur renvoyée par la
méthode est dénotée par \result. On notera également que l'on utilise dans la quantification universelle le type int, qui
désigne ici les entiers mathématiques, et non le type int de Java.
Syntaxe des annotations
La syntaxe des formules logiques utilisées dans ces annotations est donnée ci-dessous. Toute expression
Java pure, c'est-à-dire sans effet et ne contenant pas d'appel de méthode, peut être utilisée dans une annotation. Les nouveaux opérateurs
sont essentiellement l'implication (==>), l'équivalence (<==>), la quantification universelle (\forall)
et existentielle (\exists).
formule ::= expr
| expr rel expr
| formule ==> formule
| formule <==> formule
| formule && formule
| formule || formule
| \forall type ident ; formule ; formule
| \exists type ident ; formule ; formule
rel ::= == | != | <</tt> | <= | > | >=
Les priorités des connectives logiques sont, de la plus forte à la plus faible : les relations (rel), la conjonction
(&&), la disjonction (||), l'implication (==>), l'équivalence (<==>), et les
quantifications (\forall et \exists).
Annotation des boucles
Comme expliqué en cours, la preuve formelle d'un programme nécessite généralement l'annotation de ses
boucles par des invariants de boucle. Un invariant de boucle est introduit dans un commentaire précédant la boucle, par le mot clé
loop_invariant. Dans l'exemple ci-dessus, un invariant de boucle adéquat est le suivant :
/*@ loop_invariant
@ 1 <= i && i <= t.length &&
@ \forall int j; 0 <= j && j < i; res <= t[j];
@*/
for (int i = 1; i < t.length; i++)
...
Cet invariant exprime d'une part que i reste toujours compris entre 1 et t.length et d'autre part que res
est plus petit que toutes les valeurs t[0],...,t[i-1]. Notez qu'il faut écrire i <= t.length et non i
< t.length car l'invariant doit être vérifié à la fin de la dernière exécution du corps de la boucle, où i = t.length.
Pour prouver d'autre part la terminaison de cette boucle, il faut spécifier un variant, c'est-à-dire un entier naturel qui
décroît à chaque tour de boucle. Ce variant est spécifié avec le mot clé decreases. Ici t.length-i convient :
/*@ loop_invariant
...
@ decreases
@ t.length - i;
@*/
for (int i = 1; i < t.length; i++)
...
Le source complètement annoté est donc le suivant :
class Min {
/*@ requires t != null && t.length > 0;
@ ensures \forall int i; 0 <= i && i < t.length; \result <= t[i];
@*/
int getMin(int t[]) {
int res = t[0];
/*@ loop_invariant
@ 1 <= i && i <= t.length &&
@ \forall int j; 0 <= j && j < i; res <= t[j];
@ decreases
@ t.length - i;
@*/
for (int i = 1; i < t.length; i++)
if (t[i] < res) res = t[i];
return res;
}
}
Preuve automatique
Une fois le programme annoté, on peut procéder à la vérification. Pour cela, il suffit de cliquer sur le bouton
ESC dans Eclipse.
ATTENTION : Il ne faut pas oublier d'activer OpenJML pour le projet Java que vous avez crée. Cela se fait par le
menu d'Eclipse : cliquer sur JML puis "Enable JML on the project".
Normalement, le prouveur Z3 doit réussir à prouver à la fois les
invariants de boucle, les variants et que les post-conditions sont vraies. On obtient alors la fenêtre suivante, qui indique que toutes les
spécifications ont été prouvées correctes.
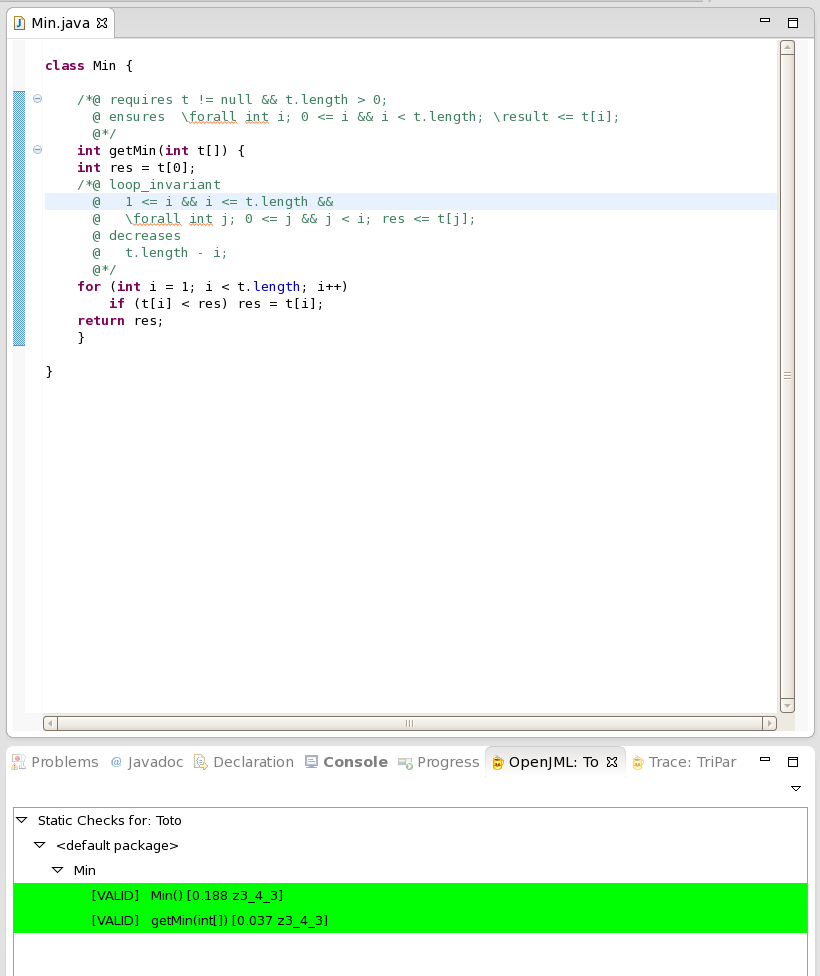
Lorsqu'une obligation n'est pas prouvée, il y a trois raisons possibles à cela :
- le programme est incorrect ; c'est là un cas satisfaisant car c'est finalement le but d'une preuve formelle que de trouver des
erreurs dans un programme.
- la spécification est incorrecte, i.e. on a incorrectement ou incomplètement spécifié le programme; c'est malheureusement
souvent le cas lorsque l'on débute la spécification formelle d'un programme.
- le prouveur n'est pas assez puissant ; c'est là presque une fatalité, la logique des prédicats du premier ordre étant
indécidable. Dans ce TD, cependant, l'objectif est de parvenir à une preuve 100% automatique. On devra donc se pencher sur les deux
premiers cas de figure avant d'envisager que le prouveur est en cause.
Utilisation de la ligne de commande.
Le plugin Eclipse d'OpenJML est parfois assez instable et les causes de bugs sont multiples. Si vous constatez que la vérification des
invariants ne fonctionne plus ou si vous obtenez des exceptions lorsque vous cliquez sur ESC, vous pouvez relancer Eclipse ou bien utiliser
la ligne de commande pour vérifier les invariants. Pour cela, vous pourrez appeler OpenJML grâce au script td7-z3 qui s'utilise ainsi:
[loire ~]$ cd workspace/TD7/src
[loire src]$ td7-z3 Ex3.java
Notez que ce script est juste un raccourci pour la ligne de commande suivante :
/users/profs/info/kaustuv.chaudhuri/jdk1.7.0_79/bin/java -jar /users/profs/info/kaustuv.chaudhuri/bin/openjml.jar -esc -exec /users/profs/info/kaustuv.chaudhuri/bin/z3 Ex3.java
Si OpenJML arrive à prouver toutes les assertions, il n'affiche rien dans le terminal. Sinon, il souligne les assertions qu'il n'arrive
pas à prouver.
Exercices
Le but de ce TP est d'écrire des annotations de fonctions et de boucle et de faire en sorte qu'elles soient toutes
vérifiées par le mode ESC d'OpenJML.
On commence par quelques exercices d'annotation de boucles. On écrira chaque exercice dans un fichier source différent.
- Prouver la terminaison des deux boucles suivantes en complétant l'assertion decreases :
static void loop1(int n) {
//@ decreases ...;
while (n > 0) n--;
}
static void loop2(int n) {
//@ decreases ...;
while (n < 100) n++;
}
Déposer vos fichiers sources.
- On cherche maintenant à montrer que la méthode loop3 suivant renvoie toujours 0. C'est le rôle de l'assertion
ensures. Nous allons utiliser deux techniques pour cela : la vérification dynamique en utilisant le mode RAC d'OpenJML et la
vérification statique en utilisant le mode ESC.
class Ex2 {
//@ ensures \result == 0;
static int loop3(int i) {
while (i > 0)
i--;
return i;
}
}
Déposer vos fichiers sources.
- On considère une méthode all_zeros qui prend en argument un tableau d'entiers et détermine si tous ses éléments sont nuls. Le
code et sa spécification sont les suivants :
/*@ requires t != null;
@ ensures \result <==> (\forall int i; 0 <= i && i < t.length; t[i]==0);
@*/
static boolean all_zeros(int t[]) {
/*@ loop_invariant ...;
@ decreases ...;
@*/
for (int k = 0; k < t.length; k++) {
if (t[k]!=0)
return false;
}
return true;
}
Donner un invariant et un variant à la boucle for de manière à prouver la correction et la terminaison de ce programme.
Déposer vos fichiers sources.
Recherche dichotomique dans un tableau trié
Nous considérons ici le problème de la recherche dichotomique dans un tableau trié
(binary search). Étant donné un tableau t d'entiers, trié par ordre croissant, et une valeur v, on chercher à
déterminer si v apparaît dans t. Le tableau étant trié, on peut procéder par dichotomie, en divisant par deux l'espace de
recherche à chaque étape. Le programme suivant effectue cette recherche, les variables l et u délimitant l'espace de
recherche.
public class BinarySearch {
static int binary_search(int t[], int v) {
int l = 0, u = t.length - 1;
while (l <= u) {
int m = (l + u) / 2;
if (t[m] < v) l = m + 1;
else if (t[m] > v) u = m - 1;
else return m;
}
return -1;
}
}
Absence d'erreur à l'exécution
Dans un premier temps, on se contente de montrer que le programme s'exécute correctement i.e.
- qu'il ne déréférence pas de pointeur null ;
- qu'il n'accède pas au tableau t en dehors de ses bornes ;
- qu'il termine.
Pour cela, donner à la méthode binary_search une précondition exprimant que le tableau t n'est pas null et à
sa boucle while un invariant de boucle portant sur les indices l et u et un variant.
Déposer votre fichier source.
Correction
On s'intéresse maintenant à la correction de la méthode binary_search. Donner une spécification formelle à
cette méthode, c'est-à-dire une postcondition exprimant
si la valeur renvoyée est positive ou nulle alors c'est un indice où t contient v
Effectuer la vérification.
Déposer votre fichier source.
Complétude
On s'intéresse maintenant à la complétude de cet algorithme. Renforcer la précondition pour exprimer le caractère trié
du tableau t :
le tableau t n'est pas null et il est trié par ordre croissant
Note : il existe plusieurs manières de spécifier qu'un tableau est trié. On préférera la forme à deux variables « pour tout i et
tout j, si i <= j alors ... » (à la forme utilisant une quantification sur une seule variable), car elle produit des
obligations de preuve plus simples, qui ne nécessitent pas de preuve par récurrence.
De même, renforcer la postcondition pour exprimer la complétude de ce programme :
si la valeur renvoyée est positive ou nulle, alors c'est un indice où t contient v; si la valeur renvoyée vaut
-1, alors v n'apparaît pas dans t; et ce sont les deux seuls cas possibles
Si l'on utilise une conjonction d'implications, on prendra soin de parenthéser correctement (la conjonction a priorité vis-à-vis de
l'implication).
Adapter en conséquence l'invariant de boucle et relancer le processus de vérification.
Déposer votre fichier source.
Tri par insertion
On se propose maintenant de vérifier la correction (partielle) d'un algorithme de tri. Il s'agit ici d'un
algorithme de tri par selection d'un tableau de n entiers. Le code Java, très simple, est le suivant :
public class Tri {
void swap (int t[],int i,int j) {
int tmp = t[i];
t[i]=t[j];
t[j]=tmp;
}
void selectionSort(int t[]) {
int mi,mv;
for (int i=0;i < t.length;i++) {
mv=t[i];
mi=i;
for (int j=i+1;j < t.length;j++) {
if (t[j] < mv) {
mi=j;
mv=t[j];
}
}
swap(t,i,mi);
}
}
}
Absence d'erreur à l'exécution
On souhaite d'abord vérifier que le code ci-dessus termine et n'effectue pas d'accès incorrect à la
mémoire. On rappelle qu'un accès à t[i] échoue si le pointeur t est nul ou si l'indice i est en dehors des
bornes du tableau t.
Dotez les méthodes swap et selectionSort d'une pré-condition, et dotez chacune des deux boucles d'un invariant, afin
de permettre à la machine de vérifier que tous les accès à la mémoire sont sûrs. (Suggestion : exigez que t soit non nul et
indiquez à quels intervalles appartiennent les indices i et j.) Dotez ensuite chacune des deux boucles d'un variant (mot
clé decreases), afin de permettre à la machine de vérifier que l'algorithme termine. Cela fait, toutes les obligations de preuve
doivent être vérifiées par le prouveur automatique.
Déposer votre fichier source.
Spécification de la fonction d'échange
On va maintenant donner une spécification complète de ce que doit faire la fonction
swap sous forme de post-condition : après l'execution de la fonction, les éléments t[i] et t[j] ont été échangés
et tous les autres éléments du tableau sont restés les mêmes. Pour écrire cette spécification, on pourra utiliser le mot clé
\old(expr) qui fait référence à la valeur de l'expression expr avant l'exécution de la méthode. Ainsi,
\old(t[i]) est la valeur de la i-ème case du tableau t avant l'exécution de swap.
Les post-conditions doivent être validées par le prouveur.
Déposer votre fichier source.
Vérification du bon ordonnancement
On souhaite maintenant vérifier que, à l'issue de la méthode selectionSort, le contenu
du tableau t est trié. En d'autres termes, on souhaite attribuer à la méthode selectionSort la spécification
suivante :
/*@ requires t != null ;
@ ensures \forall int i,j; 0<= i && i<=j && j < t.length; t[i] <= t[j];
@*/
public static void selectionSort (int[] t)
Enrichir les deux invariants de boucle de façon à ce que toutes les obligations de preuve soient satisfaites. (Suggestions : dans
la boucle externe, on pourra spécifier quelle partie du tableau est déjà triée et dans la boucle interne, on pourra montrer que la valeur
mv est la plus petite valeur de la partie non-triée de la liste. On pourra également donner la relation entre les valeurs de la
partie triée et de la partie non-triée de la liste.)
Question subsidiaire
Le résultat obtenu est intéressant, mais ne donne pas la garantie d'avoir correctement implémenté un algorithme de tri. Pourquoi ?
Pouvez-vous suggérer quel algorithme clairement incorrect satisferait notre spécification de selectionSort ?
Comment étendre la post-condition de la fonction selectionSort pour prouver que le résultat est bien le même tableau t
trié ? Essayer d'écrire ces post-conditions en JML et de les prouver. Eventuellement, on pourra imposer des contraintes (sous forme de
pré-conditions) au tableau t.
Déposer votre fichier source.






