(Luca Castelli Aleardi, Gaspard Denis and Eric Fusy)

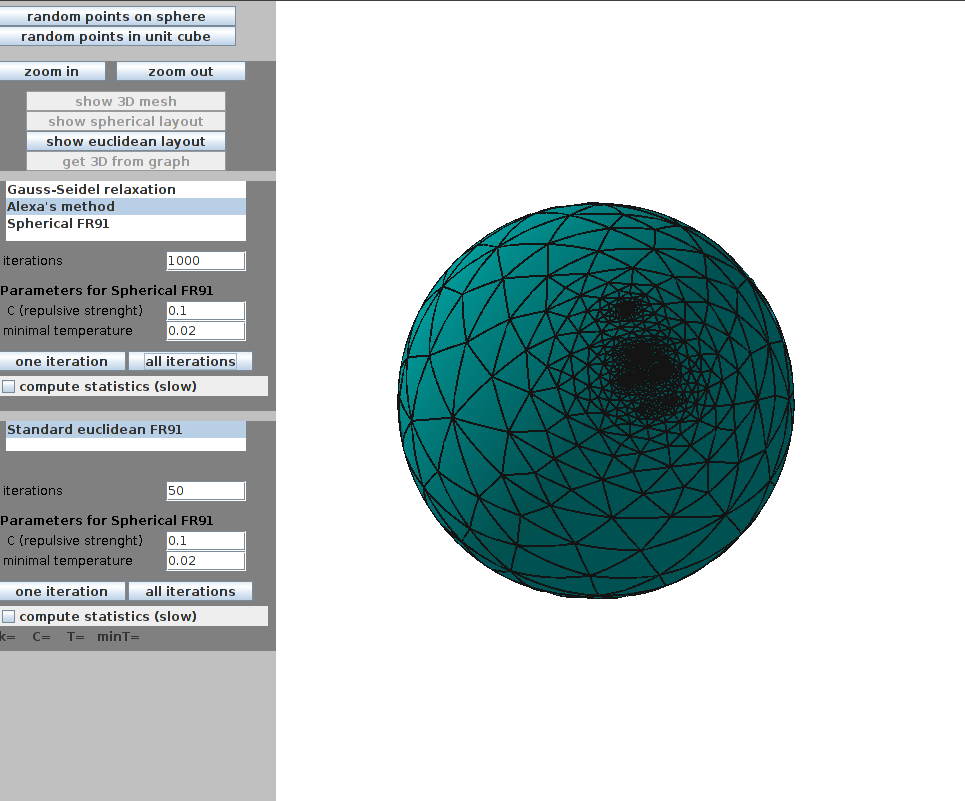
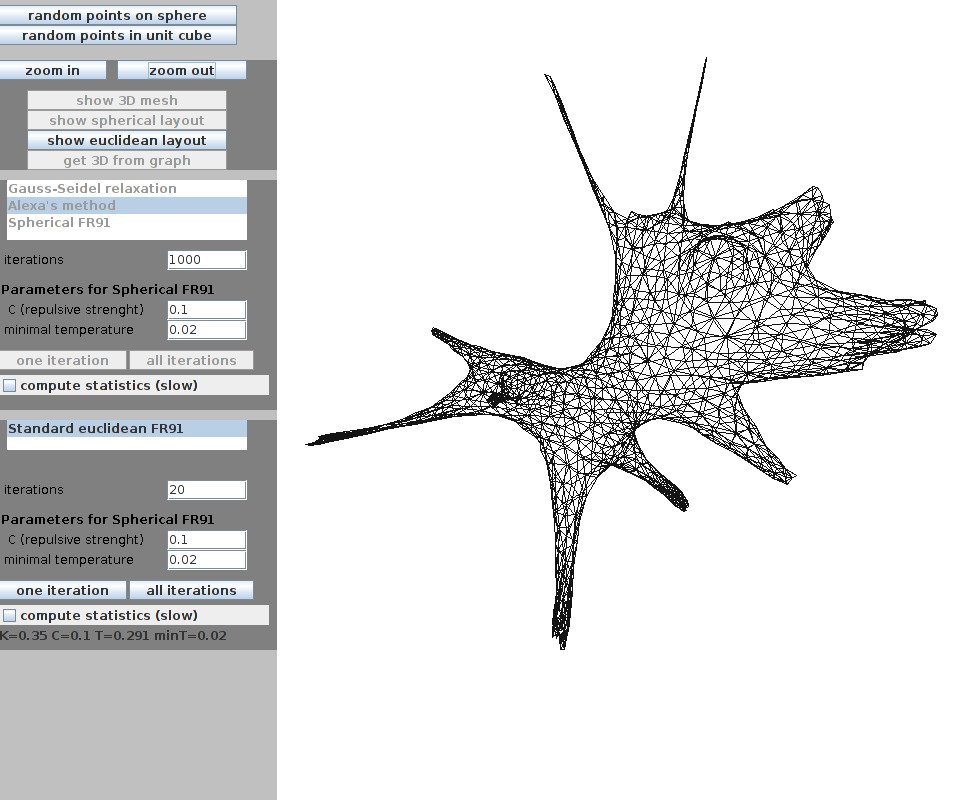
Spherical Layout computation (spherical drawing of the dog mesh)	3D Euclidean spring embedder (force-directed layout of the dog mesh)

We consider the problem of computing a spherical crossing-free geodesic drawing of a planar graph: this problem, as well as the closely related spherical parameterization problem, has attracted a lot of attention in the last two decades both in theory and in practice, motivated by a number of applications ranging from texture mapping to mesh remeshing and morphing.
Our main concern is to design and implement a linear time algorithm for the computation of spherical drawings provided with theoretical guarantees. While not being aesthetically pleasing, our method is extremely fast and can be used as initial placer for spherical iterative methods and spring embedders. We provide experimental comparison with initial placers based on planar Tutte parameterization.
Finally we explore the use of spherical drawings as initial layouts for (Euclidean) spring embedders: experimental evidence shows that this greatly helps to untangle the layout and to reach better local minima.

Data sets: initial spherical layouts

Initial Spherical Layouts (graphs stored in GEXF format)

Computation of spherical drawings of triangulations

Files to download (for running tests and benchmarks: Java 1.8 required)

• SphericalLayoutComputation.jar (compiled with Java 1.8): a runnable .jar file for running and comparing iterative methods for the computation of spherical drawings (it includes all required java libraries)
• config_InitialLayouts.txt: configuration file storing input parameters (required for running iterative schemes and force-directed methods)

Source code (Java 1.8 required)

• SphericalDrawing_src.zip: source code for the computation of spherical layouts (it includes all required java libraries and config file). The main class to run (as Java application) is: SphericalLayoutComputation (sd package)

Usage example (running from a Terminal: configuration files must be in the same location as the .jar file):

java -jar SphericalLayoutComputation.jar dog_ISP.OFF

Output example (initialization):

Spherical Layout Computation (Ecole Polytechnique, 2017) Reading a mesh from file in OFF format (shared vertex representation): data_InitialLayouts/dog_ISP.off Reading vertices...done 1480 vertices Reading face degrees...done 2956 faces Mesh loaded from OFF format (0.258170796 seconds) Building a (pointer based) halfedge representation of a surface mesh...done (0.014498226 seconds) Checking Polyhedron...ok Closed mesh: no boundaries The mesh is pure triangle n: 1480 e: 4434 f: 2956 b:0 genus: 0 Checking Polyhedron...ok ... ... ...

Output example (running 100 iterations of Alexa's method, with statistics):

... ... ... Selected (spherical) layout: Alexa 0 72.42 0.873 0.902 false 10 60.345 0.851 0.914 false 20 56.265 0.847 0.923 false 30 53.894 0.855 0.929 false 40 52.364 0.858 0.93 false 50 51.329 0.859 0.93 false 60 50.601 0.859 0.93 false 70 50.063 0.858 0.928 false 80 49.656 0.857 0.927 false 90 49.344 0.856 0.926 false