


Next: Bibliography
Up: A multi-tape S-attributed grammar's
Previous: S-attributed context-free grammars
We extend now this formalism in order to use a ``m-tape'' alphabet.
Definition 4
(
 -tape index
-tape index)
A m-tape index
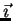
is a vector of
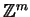
. the notation
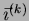
will denote the k-th
tape. We shall say that a m-tape index
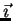
is
inferior to a m-tape index
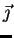
if this order stands
on every tape, and we shall denote this relation by
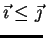
.
The  -tape index
-tape index 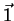 has the value 1 on all tapes. The sum of
two
has the value 1 on all tapes. The sum of
two  -tapes indexes
-tapes indexes
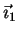 and
and
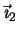 is a
is a  -tape index
-tape index
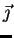 defined by
defined by
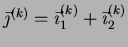 . Thus,
. Thus,
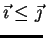 also means
also means
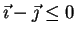 .
.
Definition 5
(
 -tape input string
-tape input string)
Given m alphabet
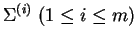
, a

-tape
input string is a vector of

strings
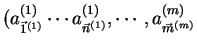
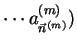
, where each string
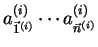
belongs to
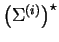
. We shall denote the set of such
defined input strings by
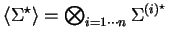
.
As a shorthand, any m-tape input string
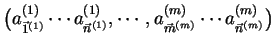
may be denoted by
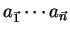
. Substrings of
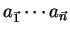
will be
denoted by
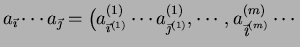
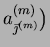
with the
usual conventions that
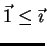
,
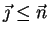
and, if
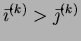
,
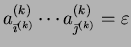
.
Example 2 (abba,dcd)
is a 2-tape input string on
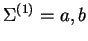
and
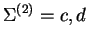
. We shall also write this 2-tape input string
as
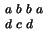
, which a somewhat more
natural notation in the context of alignments. This 2-tape input
string
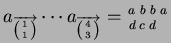
has a 2-tape input string
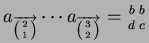
.
Definition 6
(
 -tape alphabet
-tape alphabet)
A

-tape alphabet
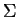
is a product of

alphabets
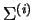
augmented with the empty string:
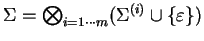
.
Definition 7
(
 -tape alignment
-tape alignment)
An element
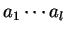
of the free monoid
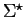
,
generated by formal concatenation of

-tape elements of
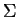
, is
called a

-tape alignment of length
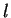
. The empty alignment of
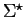
is denoted by
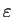
.
Definition 8
(
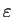 -deletion
-deletion)
Given any

-tape alignment
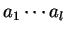
, we get a

-tape input
string
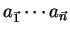
by concatenation of symbols of
the projection of
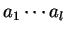
on every tape.
Example 3
The 2-tape input string
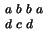
may be defined as an
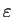
-deletion of the alignments
![$ \left\langle
\left[ \varepsilon \atop b \right]
\left[ a \atop \varepsilon \right]
\left[ b \atop \varepsilon \right]
\left[ b \atop c \right] \right.$](img85.png)
![$ \left. \left[ a \atop d \right]\right\rangle$](img86.png)
or
![$ \left\langle
\left[ a \atop \varepsilon \right]
\left[ b\atop d \right]
\left...
...ight]
\left[ b \atop \varepsilon \right]
\left[ a \atop d \right]
\right\rangle$](img87.png)
.
Once the  -tape alphabets and strings have been defined, we
naturally extend a context-free grammar into a
-tape alphabets and strings have been defined, we
naturally extend a context-free grammar into a  -tape context-free
grammar.
-tape context-free
grammar.
Definition 9
(
 -tape context-free grammar
-tape context-free grammar)
A

-tape context-free grammar
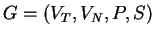
is classical
context-free grammar such that
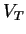 is a subset of a
is a subset of a  -tape
alphabet
-tape
alphabet.
Notice that in  -tape case,
-tape case, 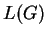 is not the set of
derivable strings but the set of
is not the set of
derivable strings but the set of
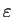 -deleted such
strings.
-deleted such
strings.
Example 4
The following toy MTCFG will align two properly parenthesized strings
interspersed with a's:
In this MTSAG, the structure defined by parentheses must be the same
on both tapes, but substrings of
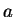
may be aligned with gaps
(denoted with
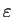
).
Then, as in mono-tape case, a  -tape context-free grammar can be
extended into a
-tape context-free grammar can be
extended into a  -tape S-attributed grammar by addition of
attributes and functions to compute the non-terminal attributes.
-tape S-attributed grammar by addition of
attributes and functions to compute the non-terminal attributes.
Definition 10
(
 -tape S-attributed grammar
-tape S-attributed grammar)
A

-tape S-attributed grammaris denoted by
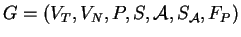
. It is an extension of a

-tape context-free
grammar
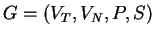
, where an attribute
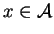
is
attached to each symbol
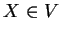
and a string of attributes
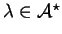
to each string
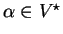
.
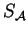
is a function from
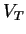
to
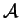
assigning attributes to
terminals.
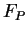
is a set of functions from
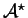
to
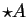
. A function
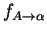
is in
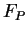
iff
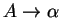
is in P.



Next: Bibliography
Up: A multi-tape S-attributed grammar's
Previous: S-attributed context-free grammars
Jerome Waldispuhl
2002-12-18
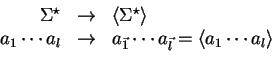
![$\displaystyle S \rightarrow \left[ {( \atop (} \right] S \left[ {) \atop )} \ri...
...arepsilon} \right]
\big\vert \left[ {\varepsilon \atop a} \right]
\big\vert SS
$](img88.png)