About the research of the order of a system of arbitrary ordinary differential equations

Published by C.W. Borchardt¹ from the posthumous manuscripts of the ill. C.G.J. Jacobi.

(Borchardt Journal für die reine und angewandte Mathematik, Bd 64, p. 297-320)²

1.
The research is reduced to the resolution of a problem of inequalities

A system of ordinary differential equations is non canonical³ if the highest derivatives of independent variables appear in the equations in such a way that one cannot deduce their value. This makes every time that one finds equations independent from these highest derivatives, either in the system itself, or after it by elimination. In this case, the number of arbitrary constants that makes appear a complete integration--that is the order of the system--is always less than the sum of the highest orders up to which go the derivatives of each variable in the proposed system.⁴ We know the order of the system if we arrive by differentiations and eliminations to an equivalent canonical form, in such a way that one can go back from the canonical system to the proposed one. For the sum of the highest orders up to which go the derivatives of each dependent variable in the canonical sytem will also be the order of the non canonical sytem. But to find this order, the reduction to a canonical form is not necessary: the thing may also be achieved by the following considerations.

Assume that we have between the independent variable $t$ and the $n$ dependent variables $x_{1}$, $x_{2}$, ..., $x_{n}$, $n$ differential equations

$$u_{1}=0,\ u_{2}=0,\ \dots,\ u_{n}=0,$$ (1)

and that

$${h_{k}}^{(i)}$$

is the highest order to which go in equation ${u_{i}=0}$ the derivatives of variable $x_{k}$. I first observe that the question may be reduced to the more simple one where the proposed differential equations are linear. In fact, differentiating the equations (1) we get a system of linear differential equations

$$v_{1}=0,\ v_{2}=0,\dots,\ v_{n}=0,$$ (2)

between the differentials:

$$\delta x_{1} = \xi_{1},\ \delta x_{2} = \xi_{2},\dots,\ \delta x_{n}=\xi_{n},$$ (3)

and ${h_{k}}^{(i)}$ will also be the highest order up to which go the derivatives of  ${\xi_{k}=\delta x_{k}}$ in the equation  ${v_{i}=\delta u_{i}}$⁵. We shall give of these linear differential equations (2) a complete integration if for values  ${k=1,2,\dots,n}$ we put

$$\xi_{k}=\delta x_{k} = \beta_{1}\frac{\partial x_{k}}{\pa... ...}}+ \beta_{2}\frac{\partial x_{k}}{\partial \alpha_{2}}+\dots,$$ (4)

where we denote by  ${\alpha_{1}, \alpha_{2}, \dots}$ the arbitrary constants occurring in the values of variables $x_{1}$, $x_{2}$, ..., $x_{n}$ in some complete integration of system (1) and by  ${\beta_{1}, \beta_{2}, \dots}$ the arbitray constants induced by the integration of the linear system (2). Which makes that the number of arbitrary constants in the complete integration of the proposed system (1) and of the linear system (2) is the same, or also that the two systems have the same order.

When searching for the order of the linear differential system (2), we may assume that the coefficients are constants⁶. In such a case, we secure a complete integration by a well-known method without any reduction to canonical form. Let us denote by the symbol:

$$(\xi)_{m}$$

an expression⁷

$$A_{0}\xi + A_{1}\frac{{d}\xi}{{d}t} + A_{2}\frac{{d}^{2}\xi}... ...t^{2}} + \cdots + A_{m}\frac{{d}^{m}\xi}{{d}t^{m}} =(\xi)_{m},$$

in which  ${A_{0}, A_{1}, A_{2}, \dots, A_{m}}$ are constants; the equations (2), if we assume their coefficients to be constants, will have the form:

$$\left\lbrace \begin{array}{lcc} v_{1} =& (\xi_{1})_{h_{... ...ots + (\xi_{n})_{h_{n}^{(n)}}\hfill &= 0. \end{array} \right.$$ (5)

I put in these equations

$$\xi_{k} = C_{k} e^{\lambda t},$$

where $C_{k}$ and $\lambda$ denote constants; (5) becomes

$$\left\lbrace \begin{array}{lr} 0 =& C_{1}[\lambda]_{h_{... ...ots + C_{n}[\lambda]_{h_{n}^{(n)}},\hfill \end{array} \right.$$ (6)

where

$$[\lambda]_{m}$$

denotes⁸ an entire function of the $m^{\rm th}$ order of the quantity $\lambda$.

Eliminating  ${C_{1}, C_{2}, \dots, C_{n}}$, we secure an algebraic equation whose roots produce the values that can take $\lambda$, and to each root or value of $\lambda$ corresponds a system of values $C_{1}$, $C_{2}$, ..., $C_{n}$ than one may multiply by some arbitrary constant. Taking the sum of the values of each variable $\xi_{k}$ corresponding to all roots, we get its complete value and, as the values thus obtained for each variable have the same arbitrary constants, the complete integration of equation (5) introduces as many arbitrary constants as there are values of $\lambda$. So, the order or the system of linear equations (2), or that of the proposed differential system (1) are equal to the degree of the algeraic equation defining $\lambda$. We can represent this equation in the following way

$$0 = \Sigma \pm[\lambda]_{h_{1}^{\prime}} [\lambda]_{h_{2}^{\prime\prime}} \cdots [\lambda]_{h_{n}^{(n)}},$$ (7)

and the degree of the right hand determinant will be the maximum of the $n!$ sums of the sequence

$$h_{1}^{\prime}+h_{2}^{\prime\prime}+\cdots +h_{n}^{(n)}$$

making the upper and lower indices vary in all possible ways. We have thus obtained the proposition:

Proposition I. Let

$$u_{1}=0,\ u_{2}=0,\ \dots,\ u_{n}=0,$$

be $n$ differential equations between the independent variable $t$ and the dependent variables $x_{1}$, $x_{2}$, ..., $x_{n}$ and let

$$h_{k}^{(i)}$$

be the maximal order of the variable $x_{k}$ in the equation ${u_{i}=0}$. Then, calling

$$H$$

the maximum of sums

$$h_{1}^{(i_{1})}+ h_{2}^{(i_{2})}+\cdots+ h_{n}^{(i_{n})},$$

obtained when summing for indices  ${i_{1}, i_{2}, \dots, i_{n}}$, all different the one from the other, among the indices  ${1, 2, \dots, n}$; $H$ will be the order of the proposed system of differential equations, or also the number of arbitrary constants appearing in its complete integration.

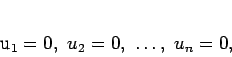
In what precedes, I call maximum a value that is not less than that of any other sum, so that many mutually equal maxima may happen, corresponding to different indices  ${i_{1}, i_{2}, \dots, i_{n}}$ of the system.

The degree of the algebraic equation (7) does not decrease, except if in the right side determinant the coefficient of the highest power of the quantity $\lambda$ vanishes.

On the other hand, we shall get the coefficient of the highest power of $\lambda$ if, when forming the determinant, we substitute to each rationnal entire function  $[\lambda]_{h_{k}^{(i)}}$ the coefficient of the highest, that is the $h_{k}^{(i)}$ $^{\hbox{\footnotesize th}}$ power that I will denote by

$$[c]_{h_{k}^{(i)}}$$

and that among all the terms of the determinant

$$\pm [c]_{h_{1}^{(i_{1})}} [c]_{h_{2}^{(i_{2})}}\dots [c]_{h_{n}^{(i_{n})}}$$

we only keep those in which the sum of indices

$$h_{1}^{(i_{1})}+ h_{2}^{(i_{2})}+\cdots+ h_{n}^{(i_{n})}$$

reaches the maximal value $H$. For never the reduction of the degree will happen, except in those cases where for two or more of the indices  ${i_{1}, i_{2}, \dots, i_{n}}$ of the system, the preceding sum reaches the same value and the sum of products

$$\pm [c]_{h_{1}^{(i_{1})}} [c]_{h_{2}^{(i_{2})}}\dots [c]_{h_{n}^{(i_{n})}}$$

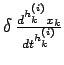corresponding to these sets of indices added with the same signs vanishes. In what precedes,  $[c]_{h_{k}^{(i)}}$ will be equal to the coefficient of the term  ${\delta\, \frac{{d}^{h_{k}^{(i)}}x_{k}}{{d}t^{h_{k}^{(i)}}}}$ coming from the variation of the function $u_{i}$, so that we will put

$$[c]_{h_{k}^{(i)}} = \frac{ \partial u_{i}}{\displaystyle \partial\, \frac{{d}^{h_{k}^{(i)}}x_{k}}{{d}t^{h_{k}^{(i)}}}}.$$

Taking this in account, appears the next proposition, which completes the first one.

Proposition II. We call ${u_{k}^{(i)}}$ the partial derivative of $u_{i}$ taken with respect to the highest derivative of $x_{k}$ contained in the function $u_{i}$ (i.e. of order $h_{k}^{(i)}$). Among all terms of the determinant  ${\pm u_{1}^{(i_{1})} u_{2}^{(i_{2})}\dots u_{n}^{(i_{n})}}$, we only keep those in which the sum of orders of derivatives of each variable, according to which in every

$$u_{1}^{(i_{1})}, u_{2}^{(i_{2})}, \dots, u_{n}^{(i_{n})}$$

partial differentiation is accomplished, reaches the value $H$. Then, if the sum of remaining terms of the determinant is denoted in this way by a determinant sign between parentheses

$$\left(\Sigma \pm u_{1}^{\prime} u_{2}^{\prime\prime} \dots u_{n}^{(n)}\right),$$

the order of the system of differential equations

$$u_{1}=0,\ u_{2}=0,\ \dots,\ u_{n}=0$$

will be less than the maximum $H$ if and only if we have

$$\left(\Sigma \pm u_{1}^{\prime} u_{2}^{\prime\prime} \dots u_{n}^{(n)}\right) =0,$$

for where the equality does not hold, the order of the system is always equal to the maximal value $H$.

We get by what precedes a new kind of formula, the truncated determinants

$$\left(\Sigma \pm u_{1}^{\prime} u_{2}^{\prime\prime} \dots u_{n}^{(n)}\right).$$

The vanishing of this quantity is the sign that the order of the system of differential equations

$$u_{1}=0,\ u_{2}=0,\ \dots,\ u_{n}=0$$

decreases⁹.

Searching for the order of a system of arbitrary differential equations, a way is to find a method for performing their reduction to canonical form¹⁰. But in this paper, we will limit ourselves to a carefull investigation of the nature of the maximum in question and the way to get it easily.

2.
About the resolution of the problem of inequalities that arises in the research of the order of the system of arbitrary differential equations. Considering a table, we define a canon. An arbitrary canon beeing given, we find a simplest one.

By what precedes, the research of the order of a system of ordinary differential equations is reduced to the following problem of inequalities, which is also worth to be proposed for himself:

Problem.

We dispose $nn$ arbitrary quantities $h_{k}^{(i)}$ in a square table¹¹ in such a way that we have $n$ horizontal series and $n$ vertical series having each $n$ termes. Among these quantities, to chose $n$ transversal, that is all disposed in different horizontal and vertical series, which may be done in ${1.2 \dots n}$ ways; and among these ways, to research one that gives the maximum of the sum of the $n$ chosen numbers.

The quantities $h_{k}^{(i)}$ beeing disposed in a square figure

$$\begin{array}{cccc} h_{1}^{\prime} & h_{2}^{\prime} & \dots ... ..._{1}^{(n)} & h_{2}^{(n)} & \dots & h_{n}^{(n)}, \\ \end{array}$$

I will call their system the proposed table. I will call derived table, every table arising from it by adding the same quantity to all terms of the same horizontal series. Let

$$l^{(i)}$$

be the quantity added to the terms of the $i$th horizontal series; doing this, each of the ${1.2 \dots n}$ transversal sums among which we need to find a maximum is increased by the quantity

$$l^{\prime}+l^{\prime\prime}+\cdots+l^{(n)} = L,$$

because in order to form these sums, we need to pick a term in each horizontal series. So that if we pose

$$h_{k}^{(i)}+l^{(i)}=p_{k}^{(i)}$$

and that the maximal transversal sum of the terms $h_{k}^{(i)}$ is

$$h_{1}^{(i_{1})}+ h_{2}^{(i_{2})}+\cdots+ h_{n}^{(i_{n})} = H,$$

this makes that the value of the maximal sum formed with the $p_{k}^{(i)}$ is

$$p_{1}^{(i_{1})}+ p_{2}^{(i_{2})}+\cdots+ p_{n}^{(i_{n})} = H+L,$$

and reciprocaly. So that finding the maximum for the quantities $h_{k}^{(i)}$ or $p_{k}^{(i)}$ is equivalent.

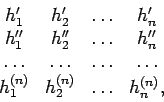
Let us do so that the quantities $l^{\prime}$, $l^{\prime\prime}$, ..., $l^{(n)}$ be determined in such a way that, the quantities $p_{k}^{(i)}$ beeing disposed in square as well as the quantities $h_{k}^{(i)}$ and chosing a maximum in each vertical series, these maxima be placed in all different horizontal series. If we call  $p_{k}^{(i_{k})}$ the maximum of terms

$$p_{k}^{\prime},p_{k}^{\prime\prime},\dots,p_{k}^{(n)},$$

the sum

$$p_{1}^{(i_{1})}+ p_{2}^{(i_{2})}+\cdots+ p_{n}^{(i_{n})}$$

will be the maximum among all the transversal sums formed with the quantities $p_{k}^{(i)}$. Indeed, in this case, we have without trouble the maximal transversal sum formed with the proposed quantities $h_{k}^{(i)}$

$$h_{1}^{(i_{1})}+ h_{2}^{(i_{2})}+\cdots+ h_{n}^{(i_{n})}.$$

So that we solve the proposed problem when we find quantities  ${l^{\prime}, l^{\prime\prime}, \dots, l^{(n)}}$ satisfying the given condition.

For short, I will call canon a square figure in which the maxima of the various vertical series are in all different horizontal series. It is clear that in such a canon, we can increase or decrease all terms by a same quantity, so that among the quantities  ${l^{\prime}, l^{\prime\prime}, \dots, l^{(n)}}$ one or more may be made equal to $0$, the others beeing positive. If ${l_{i}=0}$, the series $p_{1}^{(i)}$, $p_{2}^{(i)}$, ..., $p_{n}^{(i)}$ is the same as the orignal series  ${h_{1}^{(i)}, h_{2}^{(i)}, \dots, h_{n}^{(i)}}$, that is why I will call unchanged series, a series in the canon that corresponds to a quantity $l$ beeing zero. Among all solutions, there will be a simplest one, meaning that the quantities $l^{(i)}$ will take minimal values, so that we will find no others for which some quantities $l^{(i)}$ will take smaller values, the remaining staying unchanged. I will call the canon corresponding to that solution a simplest canon. It will be considered in what follows.

To an arbitrary square table, I associate the following denominations, which are to be well remembered: by series, I will always mean a horizontal series; dealing with a vertical one, it will be precised. By maximum, I will always mean a term maximal among all those of the same vertical, or beeing smaller than no other. So, I will call maximum of a series, a term of a horizontal series beeing maximal among all those placed in the same vertical as itself. It may happen that a series has no maximum or many different ones. And if the figure is constituted like a canon, each series certainly possesses a maximum, for if many are present in the same series, we can always sum so that all maxima of different series belong to different verticals, so that they form a complete system of transversal maxima. We will consider in a simplest canon the system of these maxima and if there are many such ones, we will chose an arbitrary one. We will then sort all the series in two parts: series $J$ and $K$, in such a way that no series $K$ is unchanged, that is none of the quantities $l$ corresponding to the series $K$ is zero. I say that we have

Theorem I. In a simplest canon, there is at least one of the maximum of series $K$ that is equal to a term located in the same vertical and belonging to a series $J$.

If not, we could decrease all the quantities $l$ related to series $K$ of a same quantity until one of these quantities, or one of the maxima of series $K$ becomes equal to a term placed on the same vertical and belonging to a series $J$. For in this way, the maxima will remain maxima and the canon structure will not be perturbed. So, the proposed quantities $l$ would not be minimal positive values nor the canon the simplest one.

If $K$ contains a single series, then the preceding theorem implies this other.

Theorem II. In a simplest canon, the maximum of some non unchanged series is equal to an other term in the same vertical.

Beeing given a simplest canon, we chose again a complete system of transversal maxima. In an arbitrary series $\alpha_{1}$, to which corresponds a non zero quantity $l$, there is a maximum to which is equal, according to $\rm II$, a term in the same vertical located in a series $\alpha_{2}$ where there is again a maximum beeing equal to a term in the same vertical from a series $\alpha_{3}$, and so on. If many terms of the same vertical are equal to a given maximum, the decribed process may be performed in various ways, but we have

Theorem III. In a simplest canon, among the various ways to go from a given series to another by the described process, there is always one by which one reaches an unchanged series, i.e. a series to which corresponds the value ${l=0}$.

For, if theorem ${\rm III}$ does not stand, we divide the series of the canon in two sets¹² the first containing all the series that can been reached by the given process and the second all those that cannot be reached, so that all unchanged series are in the second set. Doing so, we can take the first set for the series $K$ and the second for the series $J$ of theorem $\rm I$. So, according to theorem $\rm I$, we can go from a series of the first set to a series of the second, which is against our hypothesis. Hence the absurdity of the assumption that theorem ${\rm III}$ does not stand.

For brevity, I will call in the following canon  ${(m^{\prime}, m^{\prime\prime}, \dots, m^{(n)})}$ an arbitrary canon in which quantities  ${m^{\prime}, m^{\prime\prime}, \dots, m^{(n)}}$, that I assume to be always positive or zero, take respectively the place of  ${(l^{\prime}, l^{\prime\prime}, \dots, l^{(n)})}$. This defined, we shall have about two canons the

Theorem IV. Two canons beeing given, the first $(f^{\prime}$, $f^{\prime\prime}$, ..., $f^{(n)})$, the second $(g^{\prime}$, $g^{\prime\prime}$, ..., $g^{(n)})$, there will always be another canon  ${(m^{\prime}, m^{\prime\prime}, \dots, m^{(n)})}$ such that any quantity $m^{(i)}$ is smaller or equal to the smallest of $f^{(i)}$ and $g^{(i)}$.

From which follows the corollary:

The simplest canon is unique, or also there exists a unique system of quantities $l^{\prime}$, $l^{\prime\prime}$, ..., $l^{(n)}$ that gives a simplest canon.

Let the quantities  $g^{(\alpha+1)}$, $g^{(\alpha+2)}$, ..., $g^{(n)}$ be respectively greater than  $f^{(\alpha+1)}$, $f^{(\alpha+2)}$, ..., $f^{(n)}$ and $g^{\prime}$, $g^{\prime\prime}$, ..., $g^{(\alpha)}$ respectively smaller or equal to $f^{\prime}$, $f^{\prime\prime}$, ..., $f^{(\alpha)}$. We call respectively $q_{k}^{(i)}$ and $r_{k}^{(i)}$ the quantities that constitute the first and the second canon, with

$$r_{k}^{(i)}= q_{k}^{(i)} + g^{(i)} - f^{(i)},$$

and let again the system of transversal maxima in the first canon be

$$q_{1}^{(i_{1})}, q_{2}^{(i_{2})},\dots, q_{n}^{(i_{n})},$$

where the  ${i_{1}, i_{2}, \dots, i_{n}}$ are all different; in the second canon

$$r_{1}^{(i_{1})}, r_{2}^{(i_{2})},\dots, r_{n}^{(i_{n})},$$

will also be a system of transversal maxima. In fact, all the transversal sums of the second canon differ from the corresponding sums of the first by the same quantity

$$g^{\prime}+ g^{\prime\prime}+ \cdots+ g^{(n)} -\left\lbrace f^{\prime}+ f^{\prime\prime}+ \dots+ f^{(n)}\right\rbrace,$$

so, as the sum

$$q_{1}^{(i_{1})}+ q_{2}^{(i_{2})}+\cdots+ q_{n}^{(i_{n})}$$

is maximal, the sum

$$r_{1}^{(i_{1})}+ r_{2}^{(i_{2})}+\cdots+ r_{n}^{(i_{n})}$$

must be two. And as in any canon, we have by definition a maximal transversal sum whose each term is maximal among all those of its vertical, the terms

$$r_{1}^{(i_{1})}, r_{2}^{(i_{2})},\cdots, r_{n}^{(i_{n})}$$

must be respectively equal to the maxima of the first, second, ..., $n^{\rm th}$ verticals, so that their sum could be maximal. So, as $i_{1}, i_{2}, \ldots, i_{n}$ are all different one from the other, these terms constitute themselves a system of transversal maxima. Q.E.D.

As the quantities  $g^{(\alpha+1)}$, $g^{(\alpha+2)}$, ..., $g^{(n)}$ are respectively greater than  $f^{(\alpha+1)}$, $f^{(\alpha+2)}$, ..., $f^{(n)}$, quantities themselves all assumed positive or zero, the quantities  $g^{(\alpha+1)}$, $g^{(\alpha+2)}$, ..., $g^{(n)}$ are all positives. I observe then that it cannot happen that in the series $\alpha+1$, $\alpha+2$,..., $n$ of the canon $(g^{\prime}$, $g^{\prime\prime}$, ..., $g^{(n)})$ one finds a maximum equal to a term placed in the same vertical but belonging to one of the remaining series. Let in fact this maximum be in the series $i_{k}$ and the term that is equal to it in the series $i$, so that

$$r_{k}^{(i_{k})} = r_{k}^{(i)},$$

where $i$ is one of the numbers  ${1, 2, \dots, \alpha}$ and $i_{k}$ one of the numbers $\alpha+1$, $\alpha+2$, ..., $n$: we shall have according to the formula given above

$$q_{k}^{(i_{k})}+ g^{(i_{k})} - f^{(i_{k})} = q_{k}^{(i)} + g^{(i)} - f^{(i)},$$

where according to the assumption made  ${g^{(i_{k})}-f^{(i_{k})}>0}$ and  ${g^{(i)}-f^{(i)}\leq 0}$. Hence

$$q_{k}^{(i_{k})}< q_{k}^{(i)},$$

which is absurd for  $q_{k}^{(i_{k})}$ is a maximum among the terms of the same vertical  $(q_{k}^{\prime}$, $q_{k}^{\prime\prime}$, $\dots$, $q_{k}^{(n)})$. So, as in the second canon, a maximum placed in the $(\alpha+1)$ $^{\hbox{\footnotesize th}}$, $(\alpha+2)$ $^{\hbox{\footnotesize th}}$,..., $n$ $^{\hbox{\footnotesize th}}$ series cannot be equal to a term of the same vertical located in one of the remaining series, the quantities  $g^{(\alpha+1)}$, $g^{(\alpha+2)}$, $\dots$, $g^{(n)}$ may all be decreased by a same quantity, the others staying unchanged, until in one of the series $(\alpha+1)$, $(\alpha+2)$, ..., $n$ one finds a maximum not greater than the value of another term located in the same vertical, belonging to one of the remaining series or that one of the quantities  $g^{(\alpha+1)}$, $g^{(\alpha+2)}$, ..., $g^{(n)}$ vanishes. By this decreasing, no maximum, nor the nature of the canon will be destroyed. If by this mean we get

$$\left( g^{\prime}, g^{\prime\prime}, \dots, g^{(\alpha)}, g_{1}^{(\alpha+1)}, g_{1}^{(\alpha+2)}, \dots, g_{1}^{(n)}\right)$$

and that among the quantities  ${g_{1}^{(\alpha+1)}, g_{1}^{(\alpha+2)}, \dots}$, ${g_{1}^{(\beta+1)}, g_{1}^{(\beta+2)}, \dots}$ are greater than the corresponding quantities  ${f_{1}^{(\beta+1)}, f_{1}^{(\beta+2)}, \dots}$, we get by the same method a new canon in which these quantities will get a new decreasing and one can go on like this until one reaches a canon

$$\left( m^{\prime}, m^{\prime\prime}, \dots, m^{(\alpha)}, m^{(\alpha+1)}, m^{(\alpha+2)}, \dots, m^{(n)}\right)$$

where all the inclused quantitie are smaller or equal to the corresponding quantities  ${f^{\prime},\dots}$ et  ${g^{\prime},\dots}$ Q.E.D.

It follows from theorem ${\rm IV}$

Theorem V. There is no canon for which one of the quantities  ${l^{\prime}, l^{\prime\prime}, \dots, l^{(n)}}$ takes a smaller value than for the most simple canon.

Let us assume to be given such a canon, by the former method we could obtain another one for which at least one of the quantities  ${l^{\prime}, l^{\prime\prime}, \dots, l^{(n)}}$ would take a smaller value than in the simplest canon, the others beeing not greater, which is contrary to the definition of a simplest canon. As the smallest value that can take the quantities  ${l^{\prime},\dots}$ is $0$, it follows from $V$ the corollary

Theorem VI. A series beeing unchanged in some canon is also unchanged in the simplest one.

In order to know whether some canon is or not the simplest, we can add this proposition.

Theorem VII. A canon beeing given, and having chosen a system of transversal maxima, we first denote $A$ the unchanged series, then $B$ the series whose maxima are equal to a term of a series $A$ located in the same vertical, then $C$ the series whose maxima are equal to a term of a series $B$ located in the same vertical, and so on. If, continuing this process, we exhaust all the series of the canon, it will be the simplest.

The quantities  ${l^{\prime}, l^{\prime\prime}, \dots, l^{(n)}}$ are related to the proposed canon and the quantities  $l_{1}^{\prime}$, $l_{1}^{\prime\prime}$, ..., $l_{1}^{(n)}$ to some other canon. We assume to be chosen the same system of transversal maxima as in the proposed theorem, to which corresponds a system of transversal maxima in the other canon.

If  ${l_{1}^{(\gamma)}<l^{(\gamma)}}$, the maximum of the series $\gamma$ in the other canon will possess a smaller value than in the proposed canon. If the series $\gamma$ belongs to the set $C$, so that in the proposed canon, the maximum of the series $\gamma$ is equal to a term of the series $\beta$ belonging to the set $B$, then we must have  ${l_{1}^{(\beta)}<l^{(\beta)}}$. For in fact, calling $p_{k}^{(i)}$ the terms of the proposed canon and $q_{k}^{(i)}$ those of the other, we shall have

$$q_{k}^{(\beta)}=p_{k}^{(\beta)}+l_{1}^{(\beta)}-l^{(\beta)},$$

whence if  ${p_{k}^{(\gamma)}=p_{k}^{(\beta)}}$ is the maximum of the series $\gamma$, we will have

$$q_{k}^{(\beta)}=p_{k}^{(\beta)}+l_{1}^{(\beta)}-l^{(\beta)} ... ...eta)}-\left\lbrace l_{1}^{(\gamma)}-l^{(\gamma)}\right\rbrace.$$

Hence, as  $q_{k}^{(\gamma)}$ is the maximum of the $k$ $^{\hbox{\footnotesize th}}$ vertical, so that  ${q_{k}^{(\gamma)}\geq q_{k}^{(\beta)}}$ and  ${l_{1}^{(\gamma)}<l^{(\gamma)}}$, we must have  ${l_{1}^{(\beta)}<l^{(\beta)}}$.

Then, in the proposed canon, the maximum of the series $\beta$ is equal to a term of the series $\alpha$ belonging to the set $A$ and we show in the same way that we must have  ${l_{1}^{(\alpha)}<l^{(\alpha)}}$, which is absurd for, according to the made assumption, ${l^{(\alpha)}=0}$ and  $l_{1}^{\prime}$, $l_{1}^{\prime\prime}$, ..., $l_{1}^{(n)}$ are positive or zero. The reduction to absurdity proceeds in the same way, to whatever set $A$, $B$, $C$, $D$, ...may belong the series $\gamma$ to which corresponds in the other canon the quantity  $l_{1}^{(\gamma)}$ less to that of the considered canon $l^{(\gamma)}$. So, if the canon is as assumed in $\rm VII$, the values $l$ cannot take for any other smaller values; in other words, the proposed canon is the simplest.

What preceds contains the solution of the problem, an arbitrary canon beeing given, find the simplest one. We can assume that in the given canon, at least one series is unchanged; if there is none, we can get some by decreasing all the $l$ of the same quantity. As in theorem $\rm VI$, we call $A$ the set of unchanged series and build the sets ${B,C,\dots}$ there defined. If, by this process, we exhaust all series the canon is, according to ${\rm VII}$ already the simplest. Let us assume that there remain series, deprived of such maxima to which are equal terms of the same vertical belonging to the built sets. So, the terms of the remaining series (or the quantities $l$ related to these series) can be all decreased of a same quantity, until one of their quantities $l$ becomes zero or one of their maxima decreases as far as beeing equal to a term in the same vertical and belonging to the built sets. That done, we get another canon, in which the number of series belonging to the sets built according to the indicated rule is increased. If all series come in these sets, then the canon will be the simplest. If not, new canons are to be constructed by repeating the same process, always fewer series remaining outside the sets that can be built, until we secure a canon in which these sets will exhaust all the series and which is the requested simplest canon.

Example.

$$\begin{array}{cc} \hbox{\footnotesize Proposed table.} & \h... ...l 40\rlap{$^{\ast}$}&\hfill 0 \end{array}$}\hfill \end{array}$$

$$\begin{array}{cc} \hbox{\footnotesize Derived canon I.} & \... ...l 40\rlap{$^{\ast}$}&\hfill 0 \end{array}$}\hfill \end{array}$$

$$\begin{array}{c} \hbox{\footnotesize Simplest canon.} \\ \... ...21 &\hfill 40\rlap{$^{\ast}$}&\hfill 0 \end{array}\end{array}$$

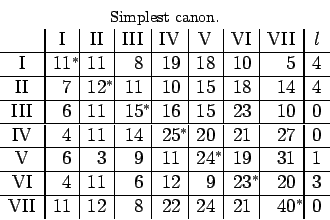
Starting from the proposed table, adding to the terms of the various series the respective numbers $5$, $8$, $3$, $1$, $5$, $6$, $0$, we get a new table, in which some maximal terms amongs all those located in the same vertical are placed in different horizontal series, which is the characteristic property of a canon.

We propose ourselves to find the simplest canon. The series VII constitutes in the given canon the set $A$. I substract unity from the terms of the remaining series, which produces the derived canon I.

In the derived canon I, the series IV and VII constitute the set $A$, the series I the set $B$. I substract $2$ from the others terms, which produces the derived canon II.

In the derived canon II, the series III, IV, VII constitute the set $A$, the series I and VI the set $B$; I substract unity from the second and fifth series, producing the last canon or simplest canon, corresponding to values of $l$ $4$, $4$, $0$, $0$, $1$, $3$, $0$. Adding these to the terms of the various series of the proposed table, we get the simplest canon. The series III, IV, VII constitute the set $A$, the series I, II, V, VI the set $B$; we see that these sets exhaust all series, which is the characteristic property of the simplest canon.

If we do not give ourselves a canon, but only the terms of the table constituting a maximal transversal sum, we reach the simplest canon by adding to each series the smallest quantity such that the term of this series belonging to the minimal transversal sum be made equal to the maximum of its vertical. Having applied this process to every series and having repeated it if necessary, we must get a canon that will be the simplest, for we do not add to the series any increment greater than what is necessary for making the given terms maximal in their respective verticals.

Example.

$$\begin{array}{cc} \hbox{\footnotesize Proposed table.} & \h... ...1 &\hfill 20 &\hfill 40\rlap{$^{\ast}$} \end{array}\end{array}$$

$$\begin{array}{c} \hbox{\footnotesize Simplest canon.} \\ \... ...1 &\hfill 20 &\hfill 40\rlap{$^{\ast}$} \end{array}\end{array}$$

The terms marked with an asterisk form a maximal transversal sum, it appears that I got the proposed table from the preceding one by changing the vertical series in horizontal ones and the verticals in horizontals; doing so, the same terms constitute a maximal transversal sum, but the table is no more an canon.

To the series

$$\rm I, II, III, IV, V,$$

I add respectively, according to the given rule,

$$8, 6, 8, 2, 7,$$

which gives the derived table.

To the series

$$\rm I, II,$$

I add respectively

$$6, 4,$$

which produces the researched simplest canon, in which the series III, IV, V, VI, VII remain the same as in the derived canon. In the obtained canon, the series VI et VII constitute the set $A$, the series III, IV, V the set $B$, the series I, II the set $C$, as these sets contain all series, we have the proof that the canon is the simplest. --

As, a canon being given, we also know a transversal sum of the proposed table, we can reduce to the problem solved by what precedes this other problem, being given an arbitrary canon, to look for the simplest. So, this will have two solutions, one by successive substractions, as above, the other by successive additions, meaning that if we deduce from the given canon a maximal transversal sum of the proposed table, we apply, this being known, the preceding method.

3.
We finish to expose the solution of the inequality problem considered in the preceding paragraph. A table being given, we find a canon.

We still have to show how to find an arbitray canon; having found one, we have seen various ways to obtain the simplest. So, we propose the following inequality problem that must be our starting point.

Problem.

Beeing given $nn$ quantities $h_{k}^{(i)}$ where the indices $i$ and $k$ take the values  ${1, 2, \dots, n}$, to find $n$ minimal positive quantities

$$l^{\prime}, l^{\prime\prime}, \dots, l^{(n)}$$

such that, having posed

$$h_{k}^{(i)}+l^{(i)}=p_{k}^{(i)},$$

and having chosen for each $k$ a maximum among the terms

$$p_{k}^{\prime},p_{k}^{\prime\prime},\dots,p_{k}^{(n)},$$

that be

$$p_{k}^{(i_{k})},$$

the indices

$$i_{1}, i_{2}, \dots, i_{n}$$

be all different the one from the other.

Solution.

A first and in some way preparatory operation consists, if there are in the table series in wich no maximum exists, to increase them of the minimal quantity doing that one of their terms becomes equal to a maximum placed in the same vertical. We get thus a new table that I call preparatory table and in which every series possess one or more maxima. It is not mandatory that all maxima of the various series of preparatory table belong to different verticals. But, at least we shall have two series whose maxima belongs to two verticals, which only appears in the limit case where all maxima are placed in the same series and all the terms of a same vertical are equal; if not, the number of transversal maxima is always $>2$. If ${n=2}$, the problem is solved by this preliminary operation.

In the preparatory table, I look for the maximal number of transversal maxima, when there are many possible choices, it is enough to consider at least one. This choice beeing made, I solve the proposed problem by successively increasing the number of transversal maxima until we get a table equipped with a complete system of transversal maxima that will be the researched canon. So, we only have to show that one can augment by one the number of transversal maxima with a suitable increasing of series.

A	C
B	D

I divide the preparatory table in four parts as in the figure in the margin. We assume that the chosen transversal maxima are all in part  $A$, so that the series where they are fill the parts $A$ and $C$; the verticals to which they belong fill the parts $A$ and $B$. I call upper the series filling parts $A$ and $C$ and lower these filling parts $B$ and $D$. I call then left the vertical filling parts $A$ and $B$ and right the verticals filling parts $C$ and $D$. Then, in part $D$ there is no maximum. If so, the number of transversal maxima would be increased, contradicting the hypothesis that it is maximal. So, the right verticals have all their maxima in $C$; the maximal terms in their own verticals of the lower series are in $B$, and every one of them will be equal to a maximum of the same vertical located in $A$, for in the space $A$ are placed the maxima of all the left verticals as well as those of all the upper series.

Granting this, I share all the series in three classes, defined as follows.

I choose these of the upper series that, besides maxima in $A$, possess even others, placed in $C$, so that at least one of these series exists. Let us assume that one of the maxima of these series placed in $A$ be equal to some other term of the same vertical; we look for a maximum placed in the same series than this term and, if it is equal to another term in the same vertical, we look again for a maximum placed in the same series as that term, and so on. All the series that one may reach in this way, from the starting series, constitute the first class.

I say that, among the series of the first class, there is neither lower series, nor upper series from which one may go to a lower series by the indicated process. For in fact, starting from a series having besides a maximum in $A$ another one in $C$, we consider a system of maxima placed in $A$ to which we have come by the indicated method, and whose last, if possible, is equal to a term in the same vertical placed in $B$. All these maxima placed in $A$ are, by hypothesis, transversal maxima and we shall get in their own place a new system of transversal maxima if we substitute to each of them an equal term placed in the same vertical. In this way, we substitute to the last maximum the term placed in $B$, without using the first series, from which we started. So, adjoining the maximum of this series placed in $C$ in order to form a new system of maxima, the number of transversal maxima will increase of a unit, which contradicts the assumption that this number was maximal.

The upper series that do not belong to the first class and from which one cannot reach by the indicated way a lower series belong to the second class. It may happen that this class is empty.

At last, belong to the third class all the lower series and all the upper series from which the indicated method gives access to lower series. So, if a term of a lower series is equal to a maximum of an upper series in the same vertical--which is always the case-- this upper series will belong to the third class. The third class, except if the table is already a canon, contains at least two series, one upper and one lower.

I will explain again what I have demonstrated about the first class by saying that, among the upper series of the third class, there is none that possess a maximum placed in $C$. I will use in the sequel that form of the proposition.

The observations made in this occasion produce at the same time a method to make appear the maximal number of transversal maxima in the preparatory table. In fact, having posed such a system of transversal maxima, as it first appears, this classification indicates if this number may be increased.

The described classification beeing done, all the third class is increased by the same quantity and the smallest that makes that a term of the series of this class reaches a maximal term placed in the same vertical and belonging to a series of the first or second class.

So, if the maximum belongs to the first class, the number of transversal maxima may be increased. Let in fact be an upper series that posses, besides a maximum in $A$ another one in $C$ and from where one may go by the indicated way to a lower series. That series is to be counted in the number of upper series whereas we need to increase that of left verticals with the right vertical where stands that maximum placed in $C$. If the term of a series in the third class, equal to a maximum of a series of the first, is located in $D$, the transversal maxima remain unchanged: we only have to add this term. And if that term is in $B$, we need change all the maxima forming that chain by which we get down to the lower series from the series containing the maximum in $C$. Namely, each of these transversal maxima is to be replaced by the term in the same vertical that is equal to it, and the last by the term in $B$, a new transversal maxima appearing so by adding at the beginning the term of the first series¹³, as I have noticed about the first class.

If the maximum to which is equal a term of the third class is placed in a series of the second, nothing changes, except that these series go to the third class together with all the remaining series of the second class from which, by the indicated chain, one goes to that series. Repeating this operation again, whether we increase the number of transversal maxima or we decrease that of the second class series, unless before the number of transversal maxima is increased, we get a table deprived of second class series, because they all went to the third. But then, by the given process, we get undoubtedly an increasing of transversal maxima. Having obtained it, we need in the different cases that may arise and that would be to long to enumerate, to operate a new repartition of transversal maxima in the indicated three classes, and, that beeing done, to repeat the operation until we get a canon in which all lower series will become upper and right verticals left.

And by the method previously described, we get non only a canon, but a simplest one. To prove it, I will show that the quantities by which are increased the series are minimal, because they are required to produce any canon. And first, as regards the preparatory process, I notice that each term of the canon is greater or equal to the corresponding term of the given table, the canon beeing obtained by adding to each series of the table only positive or zero quantity. So, the maximum in each vertical of the canon is greater or equal to the maximum in the same vertical of the given table. Now, in the canons, there is in each series a maximum, so a term that is greater or equal to the maximum of the given table placed in the same vertical; so, we need to increase each series of the given table, deprived of a maximum of a quantity such that one of its terms becomes greater of equal to the maximum of the same vertical. So, if we consider the quantities by which term of a series differs from the maxima of the same vertical, the quantity by which the series must be increased cannot be less to the minimum of these quantities. So, increasing each series deprived of a maximum of the minimal quantity that will make one of its term equal to the maximum of the same vertical, these series will certainly not be increased by a quantity greater than what is required to build the canon.

The preparation beeing done, if it produces already a canon by itself, this one is certainly the simplest; we have seen in fact that positive quantities, minimal to produce a canon, are added to the series of the given table. But if a canon has not yet arisen, we had to proceed to the three classes partition. I will show now that, to produce a canon, it cannot be that one series of the third class remains unchanged.

During the demonstration, I will call $S$ the preparatory table, $K$ the obtained canon. I always assume that the classification of series has required to consider in $S$ a system of transversal maxima in the space $A$, so that if there are many such systems in $A$, any of them is to be chosen. Likewise in $K$, I assume if many systems of tranversal maxima arise, that one has been chosen.

We will consider in $S$, if any, the set of all the unchanged upper series of the first class, that is those to which nothing is added to form the canon $K$, or also those beeing the same in $S$ and $K$. We will call $H$ the set of these series and we consider transversal maxima of these, chosen in $S$ and $K$. I say that the systems of these maxima in $S$ and $K$ will be in the same verticals. Let in fact $M$ be one of these maxima in $K$ placed in an unchanged series, an equal term of the same series, itself maximal in its vertical, will correspond to it in $S$. For, as we go from $C$ to $K$ by positive additions, the terms of this vertical in $S$ are smaller of equal to the corresponding terms in $K$; so if their maximum in $K$ is equal to a term of $S$ in the same vertical, this one must be all the more maximal between the terms in the same vertical in $S$. As, according to the properties of the classes, an upper series of the third class has no maximal term placed in the same vertical in $C$, the term $M$ must belong to the space $A$. We call $V$ the set of verticals in which stand the maxima of the series of $H$ in $S$ and we assume that the vertical in which is $M$ does not belong to the verticals of $V$. There will exist in $S$ in this vertical a maximum ${N=M}$ belonging to the transversal maxima chosen in space $A$ and that is why this maximum $N$ will be placed in a series that does not belong to $H$. The chosen transversal maxima chosen in the series $H$ are themselves in the verticals of $V$, whereas $N$ is assumed to be in a vertical not belonging to $V$. This new series¹⁴ must be an upper series belonging to the third class; the maximum $N$ belongs in fact to the space $A$ and from the given definition of classes, if there is in the same vertical maximal terms all equal the one with the other, the series in which they are placed belong to the same class. Then, if in order to form the canon $K$ we would add to the series a non zero quantity the term of $K$ corresponding to $N$ would be greater than $N$, and also greater than the term $M$ placed in the same vertical, which cannot happen for $M$ is maximal in its vertical. So, this series must be itself unchanged, which is absurd for we have assumed that the series of $H$ are the set of all the unchaged series of the third class. So $M$ itself is necessarily placed in a vertical of $V$; as this is true for every maxima, it follows that the system of transversal maxima of the series of $H$ chosen in $K$ are in the same verticals than the system of transversal maxima of these same series chosen in $S$; Q.E.D.

If we take in $S$ terms corresponding and equal to the maxima of the series of $H$ in $K$, these will form in $S$ another system of transversal maxima which are in the same horizontal and vertical series. That cannot be done, unless the terms of the two systems placed in the same verticals are equal. Whence we get this corollary: if we take in $S$, in some unchanged series of the third class, a maximum, we will have in $K$ an equal maximum in the same vertical, in an upper series of the same class. I always assume that the maxima in $S$ or in $K$ are taken in the chosen systems of transversal maxima.

As for the rest, the last proposition is proved in the same way if $H$ stands for the set of series of the second class; on the other hand it is only for these that the proposition is strong and significant. Actually, there is no unchanged series of the third class.

It appears first that there is no unchanged lower series. If in fact there is some unchanged lower series, let $M$ be its maximum in $K$, taken from the chosen system of transversal maxima; this same term will in $S$ be maximal among all those of the same vertical and for that reason it is equal to a maximum from a series of the third class placed in the same vertical and belonging to transversal maxima¹⁵. But, according to the preceding corollary, there must be in $K$, in the same vertical, a maximum of an upper series belonging to the transversal maxima, whence we shall have in $K$, in the same vertical two transversal maxima, one in an upper series, the other $M$ in a lower one, what is contrary to the notion of transversal maxima.

I will now show that if there is an unchanged upper series of the third class, there is a lower one unchanged; as it is impossible, it will be proved that there is no unchanged series of the third class, neither lower nor upper.

Assume to be given an upper series of the third class, that I will denote by $s$. According to the definition of the third class, we shall have series $s$, $s_{1}$, $s_{2}$, ..., $s_{m-1}$ such that their maxima  ${M, M_{1}, M_{2}, \dots, M_{m-1}}$ that are taken from the chosen system of transversal maxima have each of them in the same vertical an equal term $N_{i}$ in the following series, the last $M_{m-1}$ beeing equal to a term $N_{m-1}$ of the same vertical in a lower series, so that $N_{i}$ and $M_{i+1}$ are both in the same series and that $M_{i}$ and $N_{i}$ are both equal and in the same vertical. Then, if an upper series $s$ of the third class is unchanged, we shall have, according to the preceding corollary a maximum in $K$ equal to $M$ itself and placed in the same vertical; whence it we be impossible to form the canon to increase the series $s_{1}$, for, if so, one would increase the term $N$ and the maximum $M$ itself, placed in the same vertical, would disappear. So, the series $s_{1}$ must remain unchanged, and one proves in the same way that each one of the series  ${s_{2}, s_{3}, \dots, s_{m-1}}$, as well as the lower series $s_{m}$, are unchanged, what we have seen to be impossible.

As, in order to form the canon no series of the third class may remain unchanged, let $f$ be the smallest quantity by which these series must be increased, so that, beeing increased by $f$, there is in the new table at least one that, in order to form the canon does not need to be increased more, but will stay unchanged. Let $g$ be the minimal quantity by which one increases the series $S$ of the third class, so that one of its terms becomes equal to the maximum of a series of the first or second class placed in the same vertical. If ${f<g}$¹⁶ and that every series of the third class $S$ are increased by  $f^{\hbox{\scriptsize\ref{Fprime} }}$, we see that in the new table, the repartition of series in classes is not modified, and that each one belongs to the same class as in $S$. So, there cannot be $f<g$; for if so, we would have a table in which would be unchanged series of the third class, which cannot be. Whence we see that the minimal quantity by which the series of the third class must be increased, so that one of their terms reaches a maximum of a series of the first or second class placed in the same vertical is smaller or equal to the smallest of the quantities by which the series of the third class must be increased to form the canon. From which follows that, according to the given rule, we do never operate additions greater than what is necessary to form the canon, and because of that, the canon obtained by our rule will be the simplest.

Example.

$$\begin{array}{cc} \hbox{\footnotesize Proposed table.} & \h... ...nderline{40}\rlap{$^{\ast}$}& \end{array}$}\hfill \end{array}$$

$$\begin{array}{cc} \hbox{\footnotesize Derived table I.} & \... ...underline{40}\rlap{$^{\ast}$}& \end{array}$}\hfill \end{array}$$

$$\begin{array}{cc} \hbox{\footnotesize Derived table {\rm II... ...\underline{40}\rlap{$^{\ast}$} \end{array}$}\hfill \end{array}$$

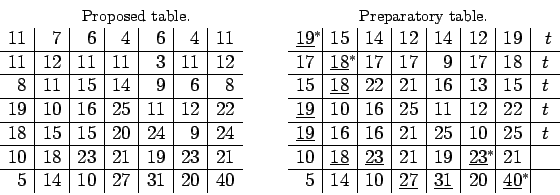
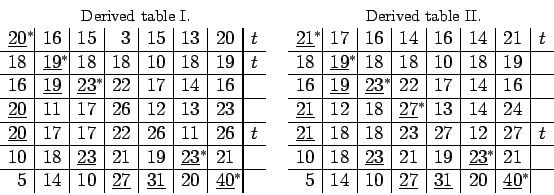
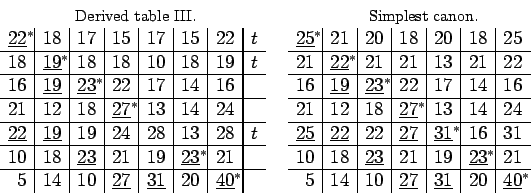
In the given table, the three first series and the fifth have no maximal terms. We need to add to these series the minimal numbers $8$, $6$, $7$, $1$, by which we can make that one of their terms becomes maximal. In the table prepared in this way, I have underlined all the maximal terms of each vertical and put a star in exponent to the chosen transversal maxima (denoted by an asterisk). At last, I have noted with a $t$ the series of the third class that we find in this way. First belong to it all the series $\alpha$ that have no starred term, that I have called above lower series; then the series $\beta$ that have a starred term in a vertical where a term of a series $\alpha$ has already been underlined; if, besides starred terms, the series $\beta$ have other underlined terms, we search in the same verticals new starred terms that belong to series$\gamma$, and so on: all the easily found series $\alpha$, $\beta$, $\gamma$ etc form the third class. It also appears that in order to fully apply the rule, we only require to know the third class series and that the repartition in first and second class is useless. For in fact the rule requires nothing more than to increase together all series of the third class of a minimal quantity such that one of their terms becomes equal to one of the maximal starred terms of other series located in the same vertical. All the work actually reduces in that increasing of series, the choice of transversal maxima and the determination of third class series, after which a new increasing is performed. Which is to be continued until one does not find any more third class series, in which case we have reached the simplest canon.

One may, by various artefacts, spare the work of rewriting the table after any change. Namely, to go from a table to the next it is not necessary to have other terms under the eyes than those beeing maximal in each vertical and those just lower, and it is enough to write only these ones. Then, it is not necessary to respect the series order, it is enough to rule out the series to be increased and to rewrite them under the unchanged ones. But these means and others that are easily used for a great amount of numbers are left to each one's choice. cm

to to 4cm