Une parenthèse. Comment mettre en équation

Un approche «mathématicienne» des problèmes considère les équations comme les données de base à partir desquelles une solution doit être recherchée. En pratique, les équations sont elles-même le résultat d'une démarche complexe, assez semblable à une traduction, où l'on s'efforce de demeurer fidèle au texte d'origine, tout en étant intelligible et si possible élégant. Parfois, la trahison est légitime, si elle est efficace.

Nous avons vu que dans certains cas, et il faut souvent simplifier pour s'y ramener, la résolution plate est plus simple que les équations «de départ», ce qui permet de se dispenser de les écrire. Tout ne saurait être aussi simple. Lorsque l'on doit écrire les équations d'un problème mécanique, la meilleure stratégie lorsque l'intuition ne nous guide pas vers une méthode plus efficace est de recourir au lagrangien. Il est en effet deux types de loi physiques, celles qui servent à comprendre, comme l'équilibre des forces, et celles qui servent à calculer, comme le principe de moindre action.

C'est ce qui fait la force du lagrangien, formule magique qui comprend à notre place les jours de petite forme. Comme toute roue de secours, elle doit savoir rester dans le coffre, quand l'imagination n'est pas en panne.

Rappelons que le langrangien d'un système mécanique est $L:=E-P$, où $E$ est l'énergie cinétique et $P$ l'énergie potentielle. Les trajectoires de la mécanique sont telles que l'action ( $\int_{t_{1}}^{t_{2}}L(x(t))dt$) est localement minimale, ce qui se traduit par les équations:

$${d\over dt} {\partial L(x,u)\over\partial x_{i}'} = {\partial L(x,u)\over\partial x_{i}},\quad i=1,\ldots,n.$$

Pour des raisons physiques, le déterminant $\left\vert\partial^{2}/\partial x_{i}\partial x_{j}\right\vert$ est non nul. Dans le cas d'une particule ponctuelle, il correspond à la masse, toujours strictement positive, etc. On peut donc déduire de ce système $n$ équation explicites d'ordre $2$ exprimant les dérivées $x_{i}''$.

La seule difficulté, mais elle est parfois réelle, est de trouver un paramétrage de l'espace d'état, qui peut avoir une géométrie complexe.

Considérons à titre d'exemple le cas d'une masse ponctuelle en mouvement sur une surface d'équation $P(x,y,z)=0$. Localement, on peut exprimer l'une des coordonnées, par exemple $z$, en fonction des deux autres. On peut alors utiliser le lagrangien comme on l'a décrit ci dessus, en posant

$$L= {1\over 2} m\left(\left(\left({\partial Z(x,y)\over \parti... ...partial Z(x,y)\over \partial y}+1\right) y'\right)^{2}\right).$$

Mais, si la trajectoire doit traverser le lieu où

$${\partial Z(x,y)\over \partial z}=0,$$

il faut choisir de nouvelles coordonnées. C'est aussi simple à concevoir en théorie que laborieux à implanter avec un solveur numérique. Une solution simple consiste à introduire une force fictive, ramenant le point vers la surface, et d'écrire

$$\begin{array}{lcl} x'' &=& -\lambda P(x,y,z){\partial P(x,y,... ...lambda P(x,y,z){\partial P(x,y,z)\over \partial z}. \end{array}$$

On peut éventuellement rajouter une force de frottement visqueux pour se ramener vers la surface, si l'on n'est pas sur de la précision des conditions initiales.

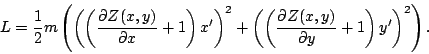
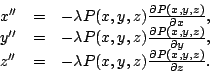
Ce type de difficulté apparaît fréquement en modélisation lorsque l'on essaye de simplifier un système en remplaçant par $0$ une quantité petite: on détruit la structure du système d'équations d'origine et l'on fait apparaître des équations algébriques difficiles à gérer. Le plus simple est souvent de ne pas trop simplifier.