Albert Girard (1590-1633), a flemish mathematician, published in 1629, in
Amsterdam, a book called Invention nouvelle en l'algèbre, in which
clear relations between roots and coefficients of polynomials were stated
for the first time. Let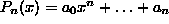 
where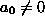 
.
Girard had the brilliant idea of postulating that such a polynomial had
to have n roots; whenever a polynomial had less than n real roots, one could
extend the set of the roots to have order n by adjoining complex
roots
. Under these conditions, one could write
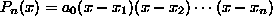where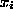 
is the 
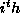root. Hence
the derivative is given by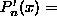 
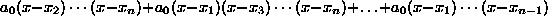
hence
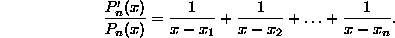
Notice that for each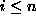 
we have
Now, provided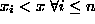 
, we have
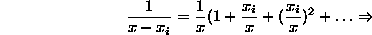
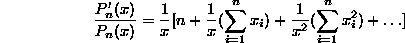
Now let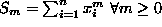 
. This means
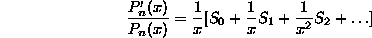
which gives infinite relations between coefficients and roots. Take for
example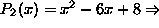 
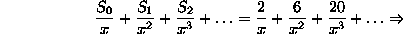
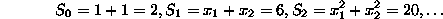
Although it is possible to derive infinitely many such relations, to isolate
one single root one needs at least a difference between some powers of the
roots. In the case of the quadratic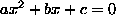 
we have
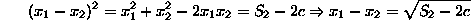
hence we can isolate the roots and solve the equation.