GOR-Arbeitsgruppe: Praxis der Mathematischen Optimierung
Prof. Dr. Josef Kallrath, Am Mahlstein 8, D-67273 Weisenheim am Berg, Tel: +49 172 747-0689, Fax: +49 621 60-6678297

We are happy to announce the 99th meeting of the GOR working group “Real World Mathematical Optimization” in the Physikzentrum Bad Honnef (Hauptstr. 5, 53604 Bad Honnef). This meeting is held as a workshop:
Distance Geometry
Inverse problems between geometry and optimization
The DG17 workshop will place on November 23-24, 2017 (Thursday and Friday). Aim at arriving on the eve of Nov. 22 if you can.
Note that the participation in a GOR-AG-Workshop for non-members is subject to a registration fee, unless you are a speaker or a host. Except for students, the Physics Center collects an infrastructure fee of 30 Euro/person.
Please register online as soon as possible, and in any case no later than October 2017. Click here for urther information about the GOR and this meeting.
Organizing committee
This symposium is about real world optimization problems involving distance geometry (DG). Consider the very easy problem: given a set of points in a Euclidean space, compute a subset of the pairwise distances. The fundamental problem in DG is the corresponding inverse problem: given a simple undirected graph with edges weighted by the distance values, as well as an integer K, compute a set of points in a K-dimensional Euclidean space which realize the given distances. The corresponding decision problem (i.e. determine whether or not there exists the realization) is called Distance Geometry Problem (DGP).
Invited speakers
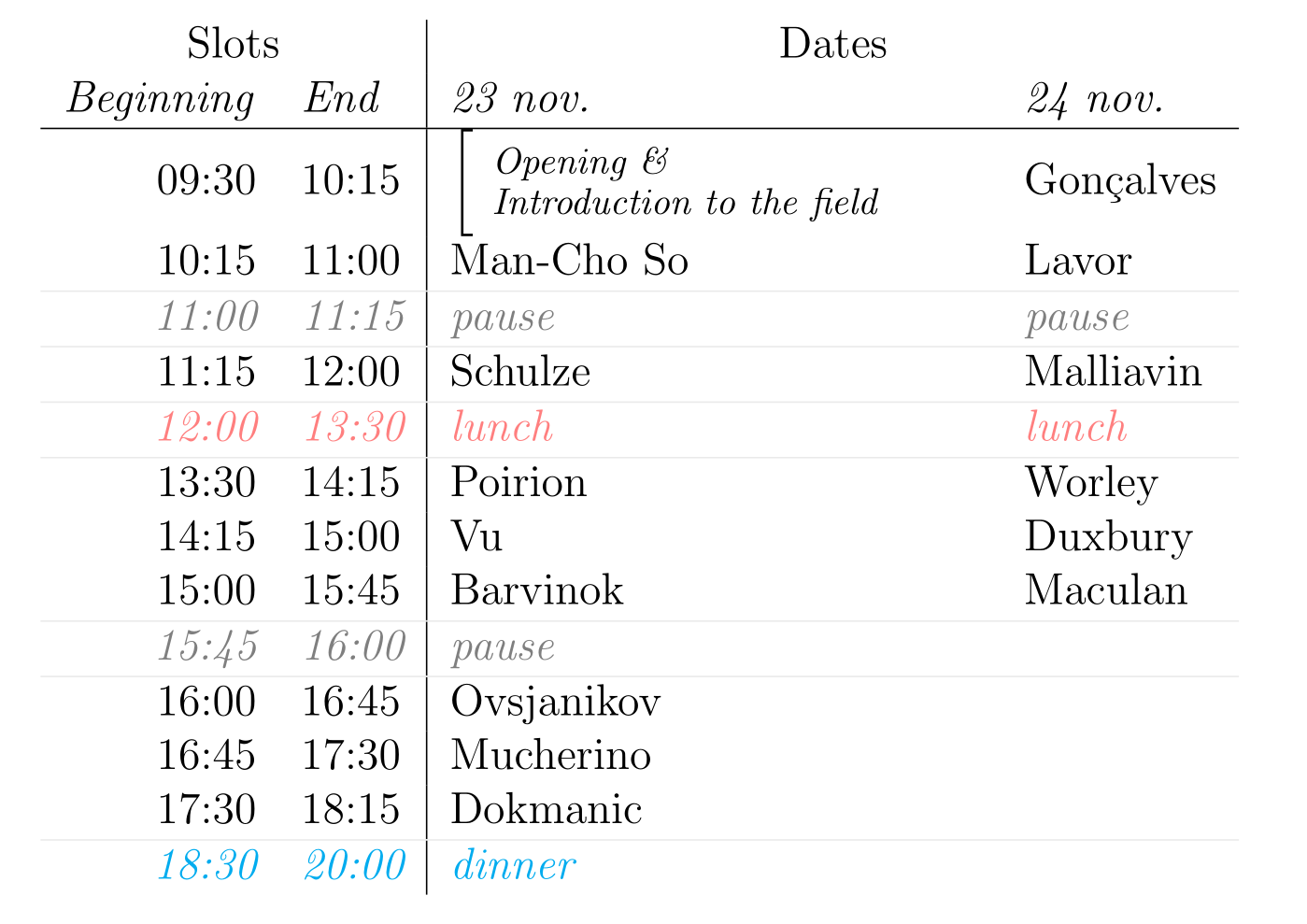
- Alexander Barvinok (University of Michigan, USA)
- Ivan Dokmanic (Univ. of Illinois at Urbana-Champaign, USA)
- Philip Duxbury (Michigan State University, USA)
- Douglas Gonçalves (Univ. Federal Santa Catarina, Brazil)
- Carlile Lavor (University of Campinas, Brazil)
- Thérèse Malliavin (CNRS and Institut Pasteur, France)
- Nelson Maculan (Univ. Federal do Rio de Janeiro, Brazil)
- Anthony Man-Cho So (Chinese University of Hong Kong, China)
- Antonio Mucherino (University of Rennes I, France)
- Maks Ovsjanikov (CNRS and Ecole Polytechnique, France)
- Pierre-Louis Poirion (Huawei Research, France)
- Bernd Schulze (Lancaster University, UK)
- Ky Vu (Chinese University of Hong Kong, China)
- Bradley Worley (Institut Pasteur, France)
Some applications of DG
The DGP is crucial in several branches of science and engineering: synchronization protocols, positioning of wireless devices, structural biology, nanotechnology, control of unmanned underwater vehicles, graph drawing, architecture and more.
- In synchronization protocols, a set of communicating devices have to exchange as little data as possible, while a central coordinating device must be able to work out the absolute time of each device in the network. This can be achieved by routing to the server the pairwise time difference for each connected device pair. The server can then reconstitute a weighted graph, and solve a DGP in one dimension in order to compute the absolute times.
- A set of wireless devices moving in an office floor can work out pairwise distances by estimating the battery used in peer-to-peer communication (the nearest the pair, the closest). The information can be synthesized in a weighted graph. Any realization of this graph in the plane (two dimensions) provides a possible positioning of the wireless sensors.
- The function of proteins is determined by both chemical configuration and geometric conformation of the atoms. Some of the inter-atomic distances can be estimated quite precisely by chemical considerations (e.g. bond lengths and bond angles will yield all weighted triangles in the graph). Other distances can be estimated using Nuclear Magnetic Resonance (NMR). This yields a weighted graph, the realization of which in three-dimensional space provides a possible conformation of the protein.
- Studying nanostructures involves a variant of the DGP, called the unassigned DGP (uDGP). In this setting, retrieving the weighted graph from the NMR data is more difficult; the input to the uDGP is simply a sequence of distance values, without reference to their adjacencies. The uDGP asks to compute the realizations of the given sequence in 3D.
- It is well known that GPS signals do not reach underwater. In a fleet of unmanned underwater vehicles focused on accomplishing a task, every submarine has to know the positions of the others at all times. They can estimate their respective distances by using their sonars; the correctness of the estimation depends on the distance itself. This yields a weighted distance graph that must be realized in 3D at each timestep.
- Graph drawing refers to the representation of graphs in vector spaces of various kinds. The DGP is a graph drawing problem in Euclidean spaces of a given dimension K, where vertices are represented by points and edges by straight segments.
- The application of architecture is somewhat different, as it does not concern the DGP proper; but, rather, the properties of the manifold of its solutions. One of the requirements of building architectural structures is that these must be able to stand even if subject to considerable external forces. Many architectural structures are modelled using bars of given length held together by devices called joints (some structures are actually built this way --- think of modern airport roofs). Weighted graphs are therefore appropriate abstract models for studying bar-and-joint architectural models. The main issue for any architectural structure is that it must not collapse. This notion, which is defined by forces acting on the bar-and-joint model, is called rigidity when applied to the weighted graph model. Although rigidity naturally applies to (graph,realization) pairs, a substantial theoretical body of research justifies the application of this notion to graphs, independently of the realization, at least in general. Graphs with finitely many realizations are rigid, while those with uncountably many realizations are flexible. Architectonically, the issue is that of having redundant rigidity the guarantee that even if some of the bars break, the building will not collapse.
The impact of DG in applied mathematics
DG has been present in many sub-fields of mathematics.
- Heron’s theorem, which establishes a fprmula for computing the area of a triangle given the side lengths, is a milestone of elementary geometry.
- L. Euler stated a famous conjecture that topologically described closed polyhedra are rigid. Cauchy gave an elegant proof of the case where the polyhedra are geometrically described as the intersection of a finite number of half-spaces, and specifically strictly convex. This proof was extended to the case of non-strictly convex polyhedra by Alexandrov. In 1978, Robert Connelly finally disproved the conjecture by exhibiting a flexible non-convex topologically described polyhedron.
- One of J.C. Maxwell’s achievements was the graphical method for solving force diagrams. The method, based on a specific notion of duality for graphs drawn in the plane, achieves the balancing of degrees of freedom assigned to points and constraints imposed by segments in a way that is reminiscent to computations using the rigiditymatrix of a graph.
- A. Cayley formalized an algebraic equation that describes the geometrical notion of a tetrahedron with zero volume. Although Cayley worked in given dimensions, his ideas are eminently generalizable. This generalization was accomplished by Carl Menger, who also developed the first unified theoretical body of work wholly on DG. Many algorithms today are based on the Cayley-Menger determinant. The work of Menger was eventually carried on by L. Blumenthal.
- The only non-logical and non-philosophical work of K. Gödel is in the field of DG. Among other things, Carl Menger was the founder of the renowned Mathematische Kolloquium in Vienna. Stimulated by DG talks given by Menger and some of his students, collaborators and seminar lecturers, responding directly to a question posed at a certain seminar, Gödel proved that if four points are realizable in 3D, then they are also realizable on the surface of a sphere with the given distances being the length of geodesic tetrahedron sides. The proof rests on a fixed-point theorem that looks more innocent than it turns out to be.
- One of the most important algorithms in data science is Multi-Dimensional Scaling (MDS). Informally, it can be described as follows: given some estimation of discrepancies between objects, it represents the object in Euclidean spaces so people can have a visual representation that helps them make informal decisions. Formally, MDS takes an approximate finite metric on n elements, turns it into an approximate Gram matrix factors it, zeros the H negative eigenvalues, and takes the transpose of the factor to produce an n𝗑H matrix representation of a realization in H dimensions. This algorithm rests on a theoretical discovery in DG made in 1935 by Isaac Schoenberg (who also invented splines), namely the formula linking each squared Euclidean Distance Matrix (EDM) D and the corresponding Gram matrix, i.e. 2B=J D J, where n J = n I – 1T1 and 1 is the all-one row vector.
- Another modern discovery used in data science and related to DG is the Johnson-Lindenstrauss Lemma (JLL). A wonderful piece of high-dimensional geometry which states something that is apparently very counter-intuitive, i.e.: for a finite set X of n points in an m-dimensional space and a given ε in (0,1) there exists a K = O(ε-2 ln n) and a K𝗑m matrix T such that, for each pair of distinct x, y in X we have (1-ε)∥x - y∥2 ≤ ∥T x - T y∥2 ≤ (1+ε)∥x - y∥2. Note that, surprisingly, the embedding dimension K is independent of the original dimension m, and only depends on the natural logarithm of the number of points in X. This discovery has been used in clustering, unconstrained optimization, statistics and is currently being applied to constrained optimization.
Aim of the workshop
This two-day event attempts to give an overview of the current state-of-the-art of DG and of the development of its practical applications. Because of the many applications fields of DG, theoretical knowledge is often mixed with the application’s practical requirements. Many similar concepts have been defined more than once, and the communities around DG are segmented by the application. Among other things, we hope to contribute to unify these communities and help them to work together.
Please contact Leo Liberti liberti at lix polytechnique fr if you are interested in attending this workshop. Attendees from universities, research institutions, industry and software companies are welcome to present selected problems and available solutions. Since talk slots are limited, we reserve the right to select speakers.
You can also contact:
Confirmed presentations
- Alexander Barvinok (University of Michigan, USA)
Convexity of the image of a quadratic map
- Ivan Dokmanic (Univ. of Illinois at Urbana-Champaign, USA)
Kinetic distance matrices
- Philip Duxbury (Michigan State University, USA)
Vector distance geometry: New reconstruction methods driven by experimental advances
- Douglas Gonçalves (Univ. Federal Santa Catalina, Brazil)
Discretizable Distance Geometry and inexact distances
- Carlile Lavor (University of Campinas, Brazil)
Conformal Clifford Algebra and the Discretizable Molecular Distance Geometry Problem
- Thérèse Malliavin (CNRS and Institut Pasteur, France)
Towards an application of the iBP algorithm to problems from structural biology
- Nelson Maculan (Univ. Federal do Rio de Janeiro, Brazil)
The Euclidean Steiner tree problem in n-space: Mixed-integer nonlinear optimization models
- Anthony Man-Cho So (Chinese University of Hong Kong, China)
Generalized Power Method for Phase Synchronization with Provable Estimation and Convergence Guarantees
- Antonio Mucherino (University of Rennes I, France)
Collaborative Dynamical Distance Geometry and Motion Adaptation
- Maks Ovsjanikov (CNRS and Ecole Polytechnique, France)
Encoding and recovering the discrete metric on triangle meshes
- Pierre-Louis Poirion (Huawei Research, France)
Random projections for SDP
- Bernd Schulze (Lancaster University, UK)
Global rigidity of periodic structures
- Ky Vu (Chinese University of Hong Kong, China)
Randomized Sketches for Large Linear System with Convex Constraints
- Bradley Worley (Institut Pasteur, France)
Towards a probabilistic model of coupled rigid motions
Costs
Accommodation and meals are provided by the Physikzentrum as a full accommodation package at the price of 135 Euro for a single-room, or 128 Euro for a double-room, respectively. This is a full board price for the whole event (including one overnight stay, meals and coffee breaks, beverages). The Physikzentrum charges an additional infrastructure fee of 40 Euro from all non-student participants. After registering, cancellations are subject to a 75 Euro cancellation fee.
Venue
The workshop takes place at the Physikzentrum Bad Honnef. Find directions to reach the Physikzentrum here.