1. P =def= a.b.P + a.c.P , Q =def= a.(b.Q + c.Q)
2. P =def= a.P + tau.P , Q =def= a.Q
3. P =def= a.P , Q =def= a.(Q | a.Q)
4. P =def= a.0 + a.P , Q =def= a.(tau.0 + tau.Q)
5. P =def= (a.b.0 | ^b.c.0)\{b} , Q =def= a.c.0
Remember that ^a represents the action complementary to a. (according to our convension, a is input and ^a is output).
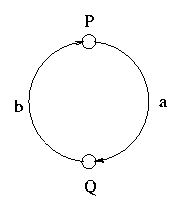
Note: You should give a finite representation of the transition graph whenever possible. For instance, if the process is P =def= a.Q and Q =def= b.P, then the graph should be:
( P1 | P2 | ... | Pn | Sem(k) )\{p,v}
The semaphore should allow at most k processes to be in the critical section.
The parameter h in Sem(h) represents the fact that h processes can still enter the critical section
(i.e. when there are no processes in the critical section then h is k, when
one process enters the critical section then h becomes k-1, etc. The processes interact with the
semaphore by performing the actions ^p (when trying to enter the critical section) and ^v (when
exiting the critical section).
The exercise consists in defining the semaphore so that it has the expected behavior.