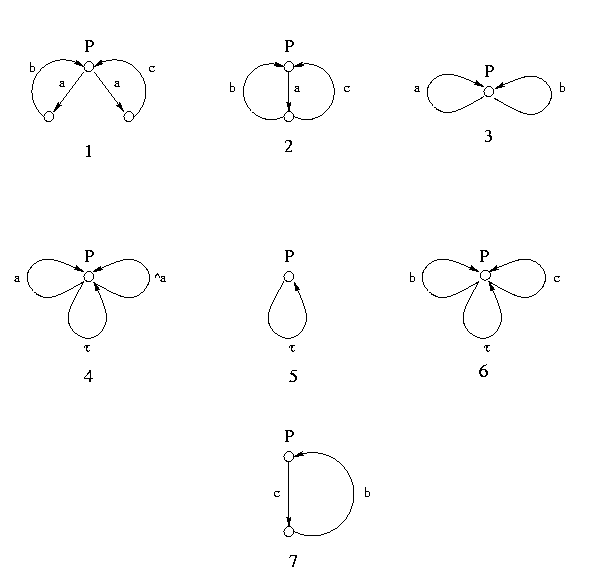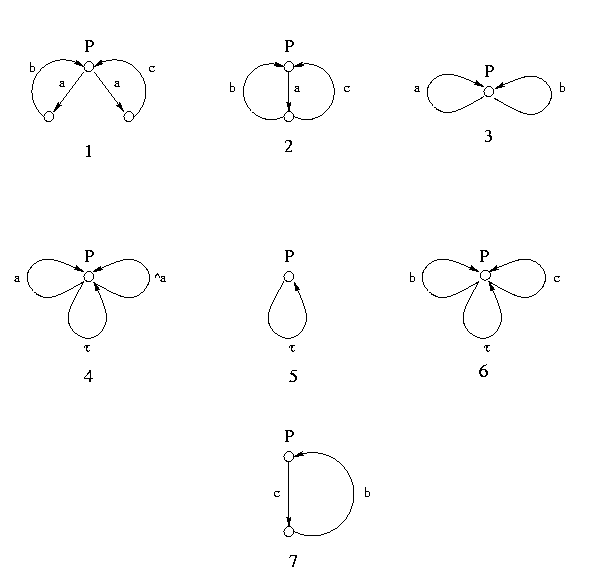Exercise 1

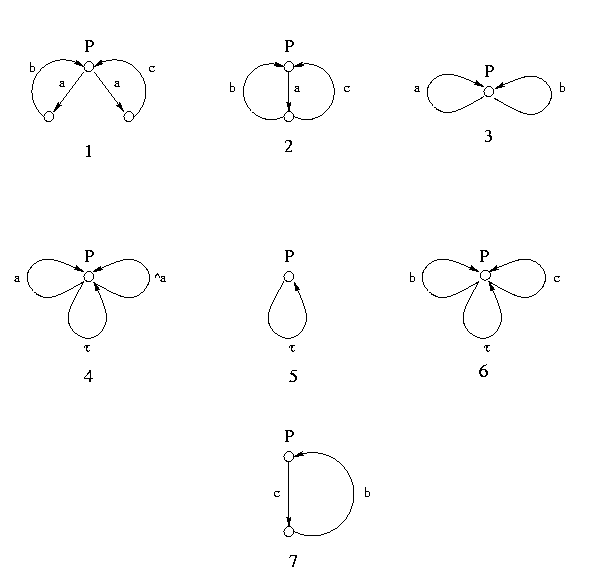
Exercise 2

1. P and Q are neither strongly bisimilar, nor weakly bisimilar. In fact P -a-> 0 while the only a-transition from Q brings to 0 + Q which is not bisimilar to 0 (because 0 + Q can make an a-transition while 0 cannot make any transition).

2. P and Q are not strongly bisimilar because P can make a tau transition and Q cannot. However P and Q are weakly bisimilar. A weak bisimulation between them is R = { (P,Q) , (0,0) }

3. P and Q are strongly bisimilar and therefore also weakly bisimilar. A bisimulation between them is R = { (P,Q) , (P|P, a.Q), (P|P|P, Q), (P|P|P|P, a.Q) ,... }

4. P and Q are neither strongly bisimilar nor weakly bisimilar. In fact, Q -a-> tau.c.0 + tau.d.0, while the only a-transitions that P can make commits either to a process that offers only a c-transition or to a process that offers only a d-transtion (after a tau-transition).

5. In general P and Q are neither strongly bisimilar nor weakly bisimilar. In fact, is R is, say, b.0, then P is able to make a b-transition after an a-transition, while Q does not have this possibility. Only if Q is equivalent to 0 then the two processes are strongly (and weakly) bisimilar.

Exercise 3