Fall 2000, CSE 520: Solution of Assignment 2

Exercise 1

The simplest solution is to use recursion:

   div(n,k) = if smaller(n,k) then 0 else div(n-k,k) + 1

The definitions of the relation "smaller" and of the function "minus" can also be given by recursion:

   smaller(n,k) = if n = 0 then (if k = 0 then false else true)
                           else smaller(n-1,k-1)

   minus(n,k) = if k = 0 then n else minus(n-1,k-1)

The rest follows the standard construction using the fixpoint operator. Thus we have:

   [div] = Y (\f n k. [if_then_else] ([smaller] n k) [0] (f ([minus] n k) k))
   [smaller] = Y (\f n k. [if_then_else] ([is_zero] n) 
                                         ([if_then_else] ([is_zero] k) [false] [true])
                                         (f ([predecessor] n) ([predecessor] k)) )
   [minus] = Y (\f n k. [if_then_else] ([is_zero] k) [n] (f ([predecessor] n) ([predecessor] k)) )

Exercise 2

-> is not confluent. In fact, consider the lambda term P =def= (\x. x x)((\y. y)R) for some lambda term R. We have that P -> M =def=(\x. x x)R and P -> N =def=((\y. y)R)((\y. y)R), but there is no common term Q to which both M and N reduce in one step. In fact, M can only reduce to Q =def= R R, while N can reduce to Q only in two steps.
-> is weakly confluent; it is an obvious consequence of the confluence of ->>.
We can also give a direct proof of this fact. Assume P -> M and P -> N. Then P must contain two different lambda redexes P₁ and P₂. If P₁ and P₂ are disjoint, then the conclusion is obvious. Otherwise, assume that P₁ is of the form P₁=def= (\x. R₁)S₁. If P₂ is inside S₁, then observe that R₁[S₁/x] ->> R₁[S'₁/x] for some term S'₁ such that S₁ ->> S'₁. If P₂ is inside R₁, then observe that R₁[S₁/x] ->> R'₁[S₁/x] for some term R'₁ such that R₁ ->> R'₁.

Exercise 3

The answer is yes. The proof can be done by induction on the number m of steps in P ->> M and on the number n of steps in P ->> N. We will prove that there exists Q such that M ->> Q in n steps and N ->> Q in m steps.
- Base case, m = 0. In this case P is the same as M (modulo alpha-conversion). Then define Q as N.
- Inductive case. Assume P ->> M in m+1 steps and P ->> N in n steps. Let R be such that P ->> R in m steps and R -> M. By inductive hypothesis, there exists S such that R ->> S in n steps and N ->> S in m steps. It can be easily proved (by induction on n and confluence of ->) that there exists T such that S -> T and M ->> T in n steps. Since we then have that N ->> T in m+1 steps, we can conclude.
Note that it is quite intuitive that the conflence of -> implies the confluence of ->>. The following diagrams illustrates the situation for n=2 and m=3 (o stands for an arbitrary term):
```
   P -> o -> o -> M
   |              .
   V              .
   o              .
   |              .
   V              .
   N .............?  Yes: 


   P -> o -> o -> M
   |    |    |    |     
   V    V    V    V
   o -> o -> o -> o
   |    |    |    |        
   V    V    V    V      
   N -> o -> o -> Q
```
The answer is no. For example, assume that the relation -> is defined in such a way that, for every P, M, and N such that P -> M and P -> N, there exists only one Q such that M ->> Q and N ->> Q, and both M ->> Q and N ->> Q take two steps. Then we can never "complete" a diagram like the one above. The following diagram illustrate the situation in the case in which P ->> N in one step and P ->> M in two steps (say, P -> R -> M). Even in this simple case we cannot close the diagram. In fact, we can find an element T such that N ->> T in two steps and R ->> T in two steps, but now we are left with the problem of closing the diagram relative to R. Since R ->> M in one step and R ->> T in two steps, the problem has the same complexity as the initial one; i.e. we are not getting any closer to the solution (we are assuming, of course, that A has enough elements to provide always new T's).
```
   P -----> R ----> M
   |                .
   |                .
   |                .
   V                .
   N ...............?  No:
 

   P -----> R ----> M
   |        |       .
   |        V       .
   |        |       .
   V        V       .
   N -->--> T ......?
```
A simpler proof is the following: Consider the following diagram

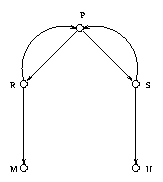
Namely, P -> R and R -> P, P -> S and S -> P, R -> M and S -> N. Then -> is weakly confluent but ->> is not confluent, in fact P ->> M and P ->> N but there is no common term to which M and N both reduce.

Exercise 4

Weakly normalizing. In fact, by reducing [is_zero] [0] and then [if_then_else] we get

   [if_then_else]([is_zero] [0]) [1] Omega -> [if_then_else] [true] [1] Omega -> [1] (normal form)

but also, by reducing Omega, we get

   [if_then_else]([is_zero] [0]) [1] Omega -> [if_then_else] ([is_zero] [0]) [1] Omega -> ...

Not normalizing. In fact, the only "evolving" reductions (i.e. reductions to a different term) bring to Omega (\y.[false]) [true] [0] [1]:

   [if_then_else]([is_zero] Omega) [0] [1] -> ([is_zero] Omega) [0] [1] 
                                           -> Omega ([true][false]) [true] [0] [1]
                                           -> Omega (\y.[false]) [true] [0] [1]

but then we have that Omega (\y.[false]) [true] [0] [1] can only reduce to itself:

   Omega (\y.[false]) [true] [0] [1] -> Omega (\y.[false]) [true] [0] [1] -> ...

Weakly normalizing. In fact, let us denote by G the term (\x.F(xx))(\x.F(xx)). Note that Y F -> G -> F G -> F(F G) ->... . We have:

   Y F [3] ->> [if_then_else] ([is_zero] [3]) [1] ([times] [3] (G ([predecessor] [3])))  
           ->> [times] [3] (G [2])
           ->> [times] [3] (F G [2])
           ->> [times] [3] ([if_then_else] ([is_zero] [2]) [1] ([times] [2] (G ([predecessor] [2]))))
           ->> ...
           ->> [times] [3] ([times] [2] ([times] [1] ([if_then_else] ([is_zero] [0]) [1] ([times] [0] (G ([predecessor] [0]))))))
           ->> [times] [3] ([times] [2] ([times] [1] [1]))
           ->> [6]   (normal form)

but also

   Y F [3] -> F G [3] -> F(F G) [3] -> ...

Note that we cannot replace G by Y F in the above formulas. In fact, although we have Y F = F(Y F) = F(F(Y F)) = ..., it is not true that Y F ->> F(Y F).

This last exercise illustrates the fact that, even in eager langauges like ML, the if_then_else operator must have a lazy semantics, otherwise recursive definition cannot be given.

Exercise 5

Of course not, for instance we have

   [true] Omega [0] -> Omega -> Omega ...

In this derivation, the first step is not monotonic. A more interesting example is the following, were every other step is not monotonic. The symbol I represents the lambda term \y.y (identity).

   (\x. I x x)(\x. I x x) -> I (\x. I x x)(\x. I x x)
                          -> (\x. I x x)(\x. I x x)
                          -> I (\x. I x x)(\x. I x x)
                          -> (\x. I x x)(\x. I x x)
                          -> ...