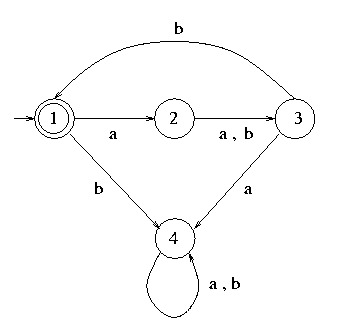

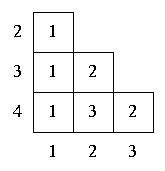
The first iteration distingues (by marking with 1) the pair of states in which one is acceptance and the other is not.
The second and third iterations distinguish (mark with 2 and 3 respectively) the pair of states for which there is a transition (with the same input) to states already distinguished in previous iteration. Thus the second transition distinguishes 2 and 3 because of the b-transition, and 3 and 4, also because of the b-transition. The third iteration distinguishes 2 and 4 because of both the a and the b transitions.
Since all states are distinguished, the FA is minimum.
We know that the minimum state FA for the language a* is the following automaton M' (where a, b, c, ... represent all the symbols of Sigma).
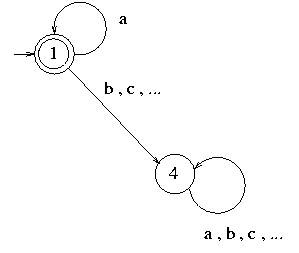
Therefore, given a FA M, it is sufficient to reduce M to its minimum-state FA M", and then check whether M" is isomorphic (namely, identical except maybe the name of the state) to M'.