Fall 2000, CSE 468: Solution of Assignment 3

Exercise 1

The minimum FA is the following:

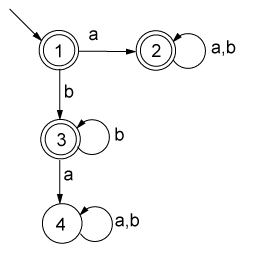
Note that the expression (a(a+b)^*b + a)^*b^* is equivalent to a(a + b)^* + b^*

Exercise 2

The regular expression is: (aba)^*
The equivalence classes associated to the indistinguishability relation are:
- [lambda] = {(aba)ⁿ | n >= 0}
- [a] = {(aba)ⁿa | n >= 0}
- [ab] = {(aba)ⁿab | n >= 0}
- [b] = {(aba)ⁿbx | n >= 0, x in {a,b}^*} union {(aba)ⁿaax | n >= 0, x in {a,b}^*}
M is not the minimum FA for L(M). The minimum FA for L(M), M', has four states only. M' can be constructed either on the basis of the partition given above, or by applying the Algorithm 5.1 in Martin's book to M. We give here the solution based on the first technique: The states of M' are: {[lambda],[a],[ab],[b]}. The initial state is [lambda], and [lambda] is also the only acceptance state. The transition relation is:
```
   Delta([lambda],a) = [a]   Delta([lambda],b) = [b] 
   Delta([a],a) = [b]        Delta([a],b) = [ab] 
   Delta([ab],a) = [lambda]  Delta([ab],b) = [b] 
   Delta([b],a) = [b]        Delta([b],b) = [b] 
```

Exercise 3

The language is not regular. This can be proved either by using the Myhill-Nerode theorem, or by using the pumping lemma. We give here the solution based on the first approach.

Consider the strings a^m and aⁿ, with m different from n. These two strings are distinguishable, in fact for z = b^m+1c a^mz is in L while aⁿz is not in L. Therefore there are infinitely many different equivalence classes associated to (the indistinguishability relation given by) L, and therefore there cannot be any FA recognizing L.